To-kropsproblem

I Kepler -problemet er banerne i de to kroppe ellipser med den samme apsidale linje , den samme excentricitet og den samme orbitalperiode omkring deres barycentre, som anses for at være fast (+). De når altid deres periapsis og apoapsis på samme tid. Ellipsernes størrelser er omvendt relateret til de to masser.

Ellipserne kan også krydse hinanden. I dette eksempel er begge masser af samme størrelse, så ellipse er også den samme størrelse.

Med passende startforhold bevæger begge legemer (her: forskellige masser) sig på cirkulære stier

I fysikken er et to-kropsproblem opgaven med at beregne bevægelsen af ​​to kroppe, der kun interagerer med hinanden uden yderligere ydre påvirkninger. De danner et to-kropssystem. Et typisk tilfælde er kollision af to kroppe, så længe alle andre muligvis eksisterende ydre kræfter kan negligeres i det mindste i kort tid. Et andet typisk tilfælde er et to-kropssystem, hvor de to kroppe tiltrækker eller afviser hinanden med en kraft, der virker parallelt med linjen, der forbinder legemerne, og hvis styrke er omvendt proportional med kvadratet af deres afstand. To eksempler på sidstnævnte tilfælde følger.

Første eksempel: To-kropsproblemet i astronomi. Den beskriver to himmellegemer, der tiltrækker hinanden med tyngdekraften . Ofte er disse objekter bundet til hinanden og bevæger sig rundt om hinanden, for eksempel i jordmånesystemet eller med dobbeltstjerner . Hvis masserne er meget forskellige, kaldes den større også for det centrale legeme .

Andet eksempel: To ladede partikler, der tiltrækkes eller frastødes af den elektrostatiske kraft . To konkrete eksempler på dette er: For det første: Proton og elektron i brintatomet , For det andet: Alfa -partikler ved kollision med en atomkerne .

Astronomi, mekanik, elektrostatik

To-kropsproblemet i astronomi er også kendt som Kepler-problemet , fordi Johannes Kepler var den første til at specificere den nøjagtige bevægelsesform for bundne to-kropssystemer i de tre love opkaldt efter ham . Dens afledning er et standardproblem i klassisk mekanik , som først blev løst af Isaac Newton .

De bevægelser, der er beregnet efter klassisk mekanik, viser sig også, når yderligere ydre kræfter virker, men disse annullerer bare hinanden for hver af de to kroppe. Et eksempel er friktionsfri glidning af to tunge kroppe på en vandret overflade, der netop neutraliserer vægtkræfterne, f.eks. B. (cirka) ved parløb på isen, eller når to glidende eller rullende kroppe støder sammen. Selvom to-kropssystemet er i et homogent tyngdekraftsfelt, gælder lovene for to-kropsproblemet i dets tyngdepunktssystem.

Med et elektrostatisk kraftfelt har Kepler -problemet de samme løsninger som med tyngdekraften. Da anvendelserne her hovedsageligt vedrører atomernes indre (se Bohr-Sommerfelds atommodel ), skal atompartiklernes kvantetype tages i betragtning. Derfor skal det kvantemekaniske to-kropsproblem løses for en tilfredsstillende fremstilling . Dette viser i tilfælde af to ikke -adskilte partikler , f.eks. B. når to elektroner eller to identiske atomkerner støder sammen, en fundamentalt anderledes adfærd end ifølge klassisk mekanik.

Det klassiske problem

Da kun de to legemer (masser , steder ) interagerer, kaldes bevægelsesligningerne ${\ displaystyle m_ {1}, m_ {2}}$${\ displaystyle {\ vec {x}} _ {1}, \ {\ vec {x}} _ {2}}$

${\ displaystyle m_ {1} {\ ddot {\ vec {x}}} _ {1} = {\ vec {F}} _ {1,2}}$

${\ displaystyle m_ {2} {\ ddot {\ vec {x}}} _ {2} = {\ vec {F}} _ {2,1}}$

Ifølge den relativitetsprincippet , kan de kræfter, kun afhænge af den relative position af de organer til hinanden. Desuden er de ifølge Newtons 3. aksiom modsat ens ${\ displaystyle {\ vec {F}} _ {1,2}, \ {\ vec {F}} _ {2,1}}$${\ displaystyle {\ vec {r}}: = {\ vec {x}} _ {1} - {\ vec {x}} _ {2}}$

${\ displaystyle {\ vec {F}} _ {1,2} = - {\ vec {F}} _ {2,1} \ =: {\ vec {F}} ({\ vec {r}}) }$

Kræfterne virker parallelt med linjen, der forbinder ligene. Således gælder krydsproduktet

${\ displaystyle {\ vec {r}} \ times {\ vec {F}} ({\ vec {r}}) = 0}$.

Overgang til det tilsvarende en-kropsproblem

Matematisk modellering af to legemers position i rummet og er positionsvektorer, der stammer fra koordinaternes oprindelse${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {x} _ {2}}$${\ displaystyle {\ mathcal {O}}}$

Du beregner nu i relative og tyngdepunktskoordinater (se figur):

${\ displaystyle {\ vec {r}}: = {\ vec {x}} _ {1} - {\ vec {x}} _ {2}}$

${\ displaystyle {\ vec {R}}: = {\ frac {m_ {1} {\ vec {x}} _ {1} + m_ {2} {\ vec {x}} _ {2}} {M }}}$( er den samlede masse.)${\ displaystyle M = m_ {1} + m_ {2}}$

Vektoren beskriver positionen af ​​det første legeme i forhold til det andet, vektoren er positionsvektoren for tyngdepunktet eller systemets barycenter . ${\ displaystyle {\ vec {r}}}$${\ displaystyle {\ vec {R}}}$

Ved at tilføje passende multipler af de to bevægelsesligninger ovenfor opnår man nu to afkoblede bevægelsesligninger:

${\ displaystyle {\ ddot {\ vec {R}}} = 0}$

${\ displaystyle {\ ddot {\ vec {r}}} = \ venstre ({\ frac {1} {m_ {1}}} + {\ frac {1} {m_ {2}}} \ højre) {\ vec {F}} _ {1,2}}$

Den første ligning siger, at tyngdepunktet beskriver en retlinet ensartet bevægelse, såvel som fra det generelle tyngdepunktsprincip udledes. Den anden ligning omformuleres til

${\ displaystyle \ mu \ {\ ddot {\ vec {r}}} = {\ vec {F}} ({\ vec {r}}),}$

hvorved

${\ displaystyle \ mu = \ left ({\ frac {1} {m_ {1}}} + {\ frac {1} {m_ {2}}} \ right) ^ {- 1} = {\ frac {m_ {1} m_ {2}} {M}}}$

kaldes den reducerede masse af to-kropsproblemet. er altid mindre end den mindste af de to masser, og nærmer sig den, når den større masse har tendens til uendelighed. Denne bevægelsesligning siger, at den relative koordinat opfører sig, som om et masselegeme bevæger sig i et stationært kraftfelt . Dette er det tilsvarende en-kropsproblem. I alle tilfælde, hvor kraftens styrke afhænger af afstandens kraft , blev den først løst af Newton. ${\ displaystyle \ mu}$${\ displaystyle {\ vec {r}} (t)}$${\ displaystyle \ mu}$${\ displaystyle {\ vec {F}} ({\ vec {r}})}$${\ displaystyle r}$

Fælles bevægelse

Tumlende bevægelse af to ulige masser omkring deres fælles tyngdepunkt (vist som en lille gul cirkel ved spidsen af ​​den stiplede linje)

Efter at en-kropsproblemet er blevet løst af banen og bevægelsen af ​​tyngdepunktet også er kendt, kan man konvertere tilbage til de originale koordinater: ${\ displaystyle {\ vec {r}} (t)}$${\ displaystyle {\ vec {R}} (t)}$

${\ displaystyle {\ vec {x}} _ {1} (t) = {\ vec {R}} (t) + {\ frac {m_ {2}} {M}} {\ vec {r}} ( t)}$

${\ displaystyle {\ vec {x}} _ {2} (t) = {\ vec {R}} (t) - {\ frac {m_ {1}} {M}} {\ vec {r}} ( t)}$

Betragtet i tyngdepunktssystemet (matematisk ved hjælp af en koordinattransformation , mere præcist en forskydning, um ), bevæger begge kroppe sig rundt om tyngdepunktet, som altid er på deres forbindelseslinje, og beskriver to kurver, der ligner kurven, hvis størrelsesforhold bestemmes af det gensidige masseforhold er. Ved at skelne mellem og indsætte to gange kan du se, at bevægelsesligningen for det første legeme ${\ displaystyle {\ vec {R}}}$${\ displaystyle {\ vec {r}} (t)}$${\ displaystyle {\ vec {x}} _ {1} (t)}$${\ displaystyle {\ vec {r}} = {\ tfrac {M} {m_ {2}}} {\ vec {x}} _ {1}}$

${\ displaystyle m_ {1} {\ ddot {\ vec {x}}} _ {1} = {\ vec {F}} _ {\ mathrm {eff}} (x_ {1})}}$

opfyldes som om kroppen befinder sig i et effektivt kraftfelt

${\ displaystyle {\ vec {F}} _ {\ mathrm {eff}} ({\ vec {x}} _ {1}) = {\ vec {F}} \ venstre ({\ frac {M} {m_ {2}}} {\ vec {x}} _ {1} \ højre)}$

ville bevæge sig hvis centrum forbliver stationært i tyngdepunktet, og hvis styrke svarer til det virkelige kraftfelt i en større afstand bestemt af masseforholdet - det samme for det andet legeme.

Hvis selve tyngdepunktet bevæger sig i en lige linje og ensartet, og yderligere egnede startbetingelser er opfyldt, beskriver de to krops baner en slags "slangekurve" omkring tyngdepunktets bane. I astronomi tillader denne såkaldte tumlende bevægelse indirekte observation af usynlige ledsagere af stjerner som z. B. Exoplaneter .

Bevaring af vinkelmoment

Kraften ligger parallelt med forbindelseslinjen (ifølge problemdefinitionen), derfor er den en central kraft og udøver ikke noget drejningsmoment på det roterende legeme, fordi dette er givet af vektorproduktet af radiusvektoren og kraften: ${\ displaystyle {\ vec {F}} _ {1,2} = - {\ vec {F}} _ {2,1} = {\ vec {F}} ({\ vec {r}})}$${\ displaystyle {\ vec {r}}}$

${\ displaystyle {\ vec {r}} \ times {\ vec {F}} = 0}$

Vinkelmomentet er derfor konstant over tid med hensyn til størrelse og retning. Det er en integreret del af bevægelse . Således foregår bevægelsen i et fast plan, fordi vektorerne og altid er i planet vinkelret på . ${\ displaystyle {\ vec {L}} = {\ vec {r}} \ times {\ vec {p}}}$${\ displaystyle {\ vec {r}}}$${\ displaystyle {\ vec {p}} = \ mu {\ vec {\ dot {r}}}}$${\ displaystyle {\ vec {L}}}$

Fra vinkelmomentets konstans følger også den 2. Kepler -lov eller områdeloven, som er gældende for hvert centralt kraftfelt.

I plane polære koordinater brydes vektor-bevægelsesligningen for etlegemsproblemet op i to koblede almindelige differentialligninger:

${\ displaystyle {\ ddot {r}} - r {\ dot {\ varphi}} ^ {2} = - {\ frac {1} {\ mu}} F (r)}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} t}} (\ mu r ^ {2} {\ dot {\ varphi}}) = 0}$

Den anden af ​​disse ligninger viser endnu engang bevarelsen af ​​vinkelmomentet , fordi ${\ displaystyle L}$

${\ displaystyle L = \ mu r ^ {2} {\ dot {\ varphi}}}$

Bevaring af energi

For Kepler -problemet i snævrere forstand er kraften givet af tyngdekraften:

${\ displaystyle F (r) = - G {\ frac {m_ {1} m_ {2}} {r ^ {2}}}}$

Hvis man bruger definitionen af ​​vinkelmomentet i polære koordinater for at eliminere vinkelhastigheden fra den anden differentialligning , opnår man en lov for afstanden , den radiale ligning${\ displaystyle {\ dot {\ varphi}}}$${\ displaystyle r}$

${\ displaystyle {\ ddot {r}} - {\ frac {L ^ {2}} {\ mu ^ {2} r ^ {3}}} = - {\ frac {1} {\ mu}} F ( r) = - {\ frac {GM} {r ^ {2}}}.}$

Dette kan gøres efter multiplikation med og i formularen ${\ displaystyle {\ dot {r}}}$${\ displaystyle \ mu}$

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} t}} \ venstre ({\ frac {\ mu} {2}} {\ dot {r}} ^ {2} + {\ frac {L ^ {2}} {2 \ mu r ^ {2}}} - {\ frac {GM \ mu} {r}} \ right) = 0}$

at blive skrevet. De tre summands i denne ligning svarer til sekvensen i henhold til radialkomponenten i kinetisk energi, den kinetiske energis vinkelkomponent, som påvirker den radiale bevægelse som centrifugalpotentiale som en potentiel energi, og kroppens potentielle energi i eksternt centralt potentiale. Sammen resulterer de i hans samlede energi

${\ displaystyle E = {\ frac {\ mu} {2}} {\ dot {r}} ^ {2} + {\ frac {L ^ {2}} {2 \ mu r ^ {2}}} - {\ frac {GM \ mu} {r}} \,}$

som ifølge ovenstående ligning er konstant over tid og derfor også en integreret del af bevægelsen. Den samlede energi skal naturligvis bevares, simpelthen fordi et tyngdefelt er et konservativt felt . Se også artiklen Specific Orbital Energy for et nærmere kig på dette.

Bane kurve

Kegleform

Hvis værdierne for bevægelsens to integraler og er givet, kan bevægelsesligningen løses ved først at beregne den radiale bevægelse ud fra formen af ​​energiintegralet (sidste ligning i afsnittet ovenfor) og derefter beregne vinkelbevægelsen fra vinkelmoment integralen. Denne vej fører imidlertid til ligninger, der kan beskrives som ikke -repræsentative , da stiens form ikke kan ses direkte fra dem. ${\ displaystyle E}$${\ displaystyle L}$${\ displaystyle r (t)}$${\ displaystyle \ varphi (t)}$${\ displaystyle L = \ mu r ^ {2} {\ dot {\ varphi}}}$

Det er derfor almindeligt at først konvertere enten radialligningen eller energiintegralet til en differentialligning efter vinklen i stedet for tiden. Så man antager som en funktion af og betragter derivatet af i forhold til vinklen . Den anden måde at bruge energiintegralet præsenteres her.${\ displaystyle \ varphi}$${\ displaystyle r}$${\ displaystyle \ varphi}$${\ displaystyle r ': = {\ tfrac {\ mathrm {d} r} {\ mathrm {d} \ varphi}} = {\ tfrac {\ dot {r}} {\ dot {\ varphi}}}}}$${\ displaystyle r}$${\ displaystyle \ varphi}$

Med energiligningen fra det foregående afsnit og ved at erstatte med og ved hjælp af vinkelmomentligningen opnår man: ${\ displaystyle {\ dot {r}}}$${\ displaystyle r '{\ dot {\ varphi}}}$${\ displaystyle {\ dot {\ varphi}}}$${\ displaystyle {\ tfrac {L} {\ mu r ^ {2}}}}$

${\ displaystyle E = {\ frac {L ^ {2}} {2 \ mu r ^ {2}}} \ venstre ({\ frac {r ' ^ {2}} {r ^ {2}}} + 1 \ højre) - {\ frac {GM \ mu} {r}}}$

Banen, der løser denne ligning, er, hvis man bruger vilkårligheden i valget af vinklen, så den største eller mindste afstand fra midten er fra formen ${\ displaystyle \ varphi}$${\ displaystyle \ varphi = 0}$

${\ displaystyle r (\ varphi) = {\ frac {p} {1+ \ varepsilon \ cos \ varphi}} \,}$

hvorved man kan beregne ved at indsætte det for de to parametre og skal gælde. Dette er ligningen for et keglesnit med numerisk excentricitet (hvor du kan vælge, fordi vekslingen svarer til ). ${\ displaystyle p = {\ tfrac {L ^ {2}} {GM \ mu ^ {2}}}}$${\ displaystyle \ varepsilon ^ {2} = {\ tfrac {2E \, L ^ {2}} {G ^ {2} M ^ {2} \ mu ^ {3}}} + 1}$${\ displaystyle \ varepsilon}$${\ displaystyle \ varepsilon \ geq 0}$${\ displaystyle \ varepsilon \ rightarrow - \ varepsilon}$${\ displaystyle \ varphi \ rightarrow \ varphi + \ pi}$

Hvis den samlede energi er negativ, så og bevægelsen er bundet, dvs. dvs. der er en maksimal afstand (apoapsis) fra midten. I dette tilfælde er kredsløbet en ellipse med et fokuspunkt i midten, hvis store halvakse er. Dette er Keplers første lov (sætning om ellipse). Det faktum, at banen for den bundne tilstand altid er lukket, er et specielt tilfælde med radialt symmetriske kraftfelter, som ellers kun forekommer med den harmoniske oscillator , hvis kraftfelt stiger proportionalt med afstanden fra midten. ${\ displaystyle \ varepsilon <1}$${\ displaystyle p / (1- \ varepsilon)}$ ${\ displaystyle a = p / (1- \ varepsilon ^ {2})}$

Hvis den samlede energi er positiv, så og kredsløbet er en hyperbola med den mindste afstand fra midten. Grænsekassen med energi og er den for en parabel, hvis mindste afstand fra centrum er. ${\ displaystyle \ varepsilon> 1}$${\ displaystyle p / (1+ \ varepsilon)}$${\ displaystyle E = 0}$${\ displaystyle \ varepsilon = 1}$${\ displaystyle p / 2}$

Energi og degeneration

Ellipsens hovedakse definerer allerede energien (beregningen herfor er lang):${\ displaystyle a}$

${\ displaystyle E = - {\ frac {GM \ mu} {2a}}}$

Derfor er alle baner med den samme hovedakse degenereret energisk, uanset hvilken excentricitet eller lille halvakse de har.

Tidsparametre

For at opnå bevægelsen over tid med en kendt vej , kan funktionen bestemmes ud fra vinkelmomentintegralet . Dette resulterer i integration på en funktion, der endnu ikke skal vendes. En beskrivende metode til at få funktionen er Kepler -ligningen fundet af Kepler . Denne metode er baseret på Keplers lov om områder, dvs. Det vil sige, at deres fysiske grundlag også er en integreret del af vinkelmomentet. Banens tidsafhængighed fører til løsningen af ​​en transcendent ligning , undtagen i særlige tilfælde og så løsningen ikke kan repræsenteres i lukket form ved hjælp af standardfunktioner. Konkret bestemmes derfor løsningen på denne ligning ved hjælp af numeriske metoder. ${\ displaystyle r (\ varphi)}$${\ displaystyle \ varphi (t)}$${\ displaystyle \ varphi (t)}$${\ displaystyle t (\ varphi)}$${\ displaystyle \ varphi (t)}$${\ displaystyle \ varepsilon = 0}$${\ displaystyle \ varepsilon = 1}$

Den periode af rotation af legemet i en elliptisk bane, på den anden side, kan bestemmes direkte af impulsmoment integral. Da ellipsens område er og også gælder, følger det: ${\ displaystyle T}$${\ displaystyle A = \ pi a ^ {2} {\ sqrt {1- \ varepsilon ^ {2}}}}$${\ displaystyle A = L / (2 \ mu) \, T}$

${\ displaystyle T ^ {2} = {\ frac {4 \ pi ^ {2} a ^ {3}} {GM}}}$

Det er præcis, hvad Keplers tredje lov siger.

Kepler -løsningen

Johannes Kepler hverken oprettede eller løste det problem, der senere blev opkaldt efter ham. Men i den kompakte form af Keplers tre love beskrev han de resulterende baner på en matematisk korrekt måde. Isaac Newton var i stand til at udgive den første løsning i 1687. Keplers love dannede en afgørende berøringssten for Newtons mekanik skabt af Newton. Strengt taget er de løsningerne på det ækvivalente étkropsproblem , hvor en tyngdekilde er fast i rummet og tiltrækker et enkelt legeme, uden at dette har nogen effekt på kilden.

Orbitale former for løsningen af ​​Kepler -problemet

Løsningen på problemet er opdelt i følgende dele:

• 1. og 2. Keplers lov (fundet 1599 til 1609, ellipsen og områdesætningen ) og
• 3. Keplers lov (1619, udgivet i Welttharmonie ).
• Den Kepler ligning .

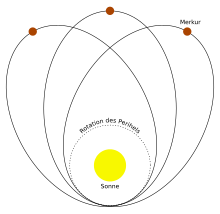
Mulige baner ( Kepler -baner ) er cirkler , ellipser , paraboler og hyperboler . Med cirkler og ellipse er kroppene bundet til hinanden som planeterne til solen. Hvis banens form er parabolsk eller hyperbolsk, finder der kun et møde sted, som det er tilfældet med f.eks. B. er tilfældet med nogle kometer .

Den tilstødende tegning viser forskellige baner. De er kendetegnet ved deres numeriske excentricitet , som er et ikke -negativt reelt tal. Har bundne stier (cirkler og ellipser) , hvor cirklen svarer til en excentricitet . Større excentriciteter fører til åbne baner (paraboler med ) og hyperboler (med ). Disse åbne stier er endnu ikke blevet nævnt af Kepler. ${\ displaystyle \ varepsilon}$${\ displaystyle \ varepsilon <1}$${\ displaystyle \ varepsilon = 0}$${\ displaystyle \ varepsilon = 1}$${\ displaystyle \ varepsilon> 1}$

For en præcis beskrivelse af et heliocentrisk planetsystem er Keplers løsning imidlertid ikke tilstrækkelig, fordi den gensidige tiltrækning af alle himmellegemer, som også blev opdaget af Newton, også er effektiv i planetsystemet. Derfor repræsenterer Kepler-problemet en fysisk idealisering . I solsystemet, som i mange andre astronomiske systemer, er indflydelsen fra de andre kroppe relativt lille, så løsningen af ​​to-kropsproblemet giver en god tilnærmelse til de nøjagtige baner . Derfor er løsningen på to-kropsproblemet grundlaget for moderne himmelsk mekanik .

Omvendt problem: kredsløbsbestemmelse

Med løsningen af ​​to-kropsproblemet er det muligt at beregne banen for to himmellegemer , som kan ses med tilstrækkelig nøjagtighed som et to-kropssystem, hvis der gives et tilstrækkeligt antal startværdier . I himmelsk mekanik står man dog normalt over for det omvendte problem : Modelparametrene (startværdier) skal beregnes ud fra den observerede bane. Med ovenstående metoder kan himmellegemernes position derefter beregnes for (nær) fremtiden, hvis de forstyrrende påvirkninger er tilstrækkeligt små.

Antallet af initialværdier, der skal bestemmes, er altid givet af det originale system med differentialligninger. Da det er en anden ordens ligning for bevægelse af to legemer i tredimensionelt rum, er disse parametre. Den form, hvori disse tolv værdier vises, afhænger imidlertid af den specifikke situation og den valgte procedure. I "brute force" -metoden til direkte numerisk integration af det oprindelige system er der for eksempel givet tre værdier for startpositionen og tre værdier for starthastigheden for hvert af de to organer. Hvis den ovenfor beskrevne analysemetode vælges, søges først tre startpositionsværdier og tre starthastighedsværdier for tyngdepunktets bevægelse. Det resterende enkelt centerproblem kræver derefter yderligere seks parametre, som klassisk er specificeret af vejelementerne : to vinkler, der definerer positionen for bevægelsesplanet i rummet (og dermed positionen for vinkelmomentvektoren), en vinkel, der beskriver banens position inden for dette plan (og dermed nulpunktet for den polare vinkel ), såvel som den store halvakse og numeriske excentricitet af den kegleformede vej (som tilsammen bestemmer energien og mængden af ​​vinkelmomentet) . Derudover skal drejelegemets startposition angives som en vinkel eller som en tidsreference ved at angive periapsistiden. En alternativ elegant metode til at specificere disse seks startværdier er at specificere to vektorer, der er konstante over tid: Vinkelmomentvektoren og Laplace-Runge-Lenz-vektoren . Disse to tredimensionelle vektorer bestemmer imidlertid ikke seks, men kun fem af vejelementerne, da vektorerne nødvendigvis er vinkelret på hinanden. Derfor skal tidsreferencen igen etableres ved at angive periapsistiden, eller der skal angives en startvinkel. ${\ displaystyle 2 \ times 2 \ times 3 = 12}$${\ displaystyle \ varphi}$

De vigtigste metoder til bestemmelse af orbitale elementer fra observationsdataene går tilbage til Isaac Newton, Pierre-Simon Laplace og Carl Friedrich Gauß .

Grænser for totrinsløsningen

To-kropsproblemet repræsenterer en idealisering, der sjældent afspejler kendsgerningerne med tilstrækkelig nøjagtighed i konkrete situationer. De eneste undtagelser er sande dobbeltstjerner uden planeter eller andre mørke ledsagere, hvis komponenter er langt nok fra hinanden til, at tidevandsvirkninger er ubetydelige. Klassiske (ikke-kvante-teoretiske) modeller af brintatomet såvel som radialt symmetriske enkelt-center spredningsproblemer kan betragtes som to-kropsproblemer .

Flere kroppe

I næsten alle virkelige situationer er der mere end to kroppe i interaktion med hinanden. Bevægelsesproblemet med flere organer kan ikke løses på en lignende måde, som dette blev præsenteret her for to kroppe. Selv tre-kropsproblemet , dvs. opgaven med at beregne kredsløbet, når interaktionen mellem et tredje legeme tages i betragtning, er normalt ikke strengt opløselig og kan kun løses numerisk generelt. Denne vanskelighed fortsætter naturligvis, når der løses problemer med flere krop med yderligere komponenter. De eneste undtagelser er stærkt symmetriske konstellationer, hvor f.eks. Legemerne danner regelmæssige polygoner, ligger på en linje eller forlænges på en skallelignende måde omkring et center. Sådanne arrangementer finder en vigtig anvendelse i undersøgelsen af ​​bevægelsen af ​​små kroppe, der er placeret i et af de fem lagrangiske punkter i et to-kropssystem.

Afvigelse fra sfærisk form

Et andet problem er afvigelsen af ​​et eller begge legemer fra den sfæriske form Mange astronomiske legemer beskrives kun upræcist ved en radialt symmetrisk massefordeling. I nogle tilfælde kan objekterne modelleres meget mere præcist, hvis de ses som flade ellipsoider af revolution. Det gælder mange planeter og stjerner, men også spiralgalakser, der let kan modelleres som flade diske. Hvis det ene af de to legemer er signifikant mindre end det andet, kan et sådant system beskrives som et aksialt symmetrisk problem med et enkelt center, som er mere generelt end det ovenfor beskrevne, men stadig er egnet til en generel løsning. Hvis begge kroppe er af sammenlignelig størrelse og ikke fladtrykt i samme retning, er denne vej også lukket. Derudover kan tidevandskræfter mellem legemerne føre til dynamiske deformationer, som det ofte er tilfældet i tætte binære stjerner. Disse fører til en kompleks dynamik mellem de enkelte legemers rotation og legemernes bevægelse omkring hinanden.

Forstyrrelsesteori

Ikke desto mindre er Kepler -løsningen grundlaget for alle moderne planeteorier (samt måneteorier og bevægelsesteorier for alle andre himmellegemer). Banerne i næsten alle naturlige objekter i vores solsystem, de fleste af flere stjerner og også galakser, er sådan, at de som en første tilnærmelse kan beskrives med Kepler -løsningen. Keplerbanernes kredsløbselementer, som bestemmes ud fra de indledende betingelser, antages da ikke længere at være konstante, men behandles i form af forstyrrelsesteori . Stielementerne, der er gyldige på et bestemt tidspunkt, beskrives derefter som oscillerende , da de bestemmer Kepler -stien, som i øjeblikket er så tæt som muligt på den rigtige vej .

Rotation af den apsidale linje ved hjælp af kviksølv -eksemplet. Stiens excentricitet og rotationsmængden er vist skematisk overdrevet.

Desuden kan påvirkningen af ​​de forstyrrende organer på to-kropssystemet ofte beregnes i gennemsnit over længere perioder, hvilket gør beskrivelsen af ​​problemet mere symmetrisk. Sådanne påvirkninger fører z. T. til tidskonstant eller periodiske ændringer i orbitalelementerne. Eksempler på sådanne fænomener er f.eks. B. den ensartede rotation af apsidallinjen , dvs. positionen af ​​Kepler -kredsløbet i kredsløbets plan og den ensartede forskydning af kredsløbsknuderne omkring et invariant plan ( Laplace -planet ). I måneteorien er yderligere eksempler på sådanne periodiske forstyrrelser evection og variation .

To-kropssystemer i generel relativitet

Den moderne tyngdekraftsteori er beskrevet i den generelle relativitetsteori (GTR). Hvis masserne af de to legemer er tilstrækkeligt små, afstandene til hinanden relativt store og legemernes hastigheder er langt under lysets hastighed , kan systemet beskrives ved teoriens Newton -grænsetilfælde. Med andre ord: Løsningen skitseret ovenfor inden for Newtons tyngdekraftsteori tilbyder en meget god omtrentlig løsning. Men hvis betingelserne for grænsesagens gyldighed ikke er opfyldt, eller kravene til nøjagtighed er meget høje, skal problemet løses inden for den fulde ART - en opgave, der viser sig at være meget mere kompliceret.

I det enkleste tilfælde, som heldigvis har mange anvendelser, har den ene af de to kroppe en meget større masse end den anden. Det er derefter berettiget at betragte det lille objekt som et testlegeme inden for det store objekt, dvs. det vil sige, den lille krop har ingen mærkbar effekt på den store. Problemet kan derefter beskrives som et generelt relativistisk single-center problem, analogt med Newtons teori . Også i GTR viser dette problem sig at være let at analysere på grund af den radiale symmetri. Bevægelsesintegraler kan findes i en lignende form som den, der er beskrevet ovenfor. Analysen fører imidlertid til en radial ligning, der indeholder et yderligere udtryk i forhold til Newtons teori, hvilket igen betyder, at banerne ikke lukkes, selv med negativ total energi . I stedet er banerne rosetbaner, som det er tilfældet for to-kropssystemer med andre kraftlove end Newtons . Denne effekt har vundet berømmelse, da den gør det muligt at forklare den ekstra perihelionrotation af Merkur.

Det generelle relativistiske to-kropsproblem generelt, dvs. med to kroppe, der interagerer med hinanden, er meget mere kompliceret. Da tilstedeværelsen af ​​de to masser ændrer selve rum-tid-strukturen, er begreber som massecenter, total energi og vinkelmoment ikke længere anvendelige. Derfor er det ikke muligt at reducere problemet til et enkelt centerproblem. Desuden er indflydelsen på rumtid forankret i den matematiske struktur ved, at problemet ikke beskrives ved almindelige differentialligninger , men ved delvise differentialligninger . Den ikke -lineære struktur af disse ligninger gør at løse ligningerne selv med numeriske metoder problematisk. I en heuristisk tilgang kan man generelt prøve at adoptere de klassiske begreber cirka. Denne beskrivelse fører til effekter som stråling af gravitationsbølger og et tilhørende "tab af vinkelmoment". Kroppernes kredsløb beskriver derefter spiralstier omkring et fælles "tyngdepunkt", som bliver tættere og tættere, når kredsløbstiden bliver kortere. Den nøjagtige beskrivelse af disse fænomener i forbindelse med en post-newtonsk tilnærmelse er kontroversiel på grund af de uforklarlige konvergensegenskaber ved tilnærmelserne.

Fodnoter

1. ↑ I de fleste tilfælde udføres substitutionen også , således at følgende differentialligning opnås: ${\ displaystyle u: = 1 / r}$

   ${\ displaystyle E = {\ frac {L ^ {2}} {2 \ mu}} \ venstre (u ' ^ {2} + u ^ {2} \ højre) -GM \ mu u}$

2. ↑ Årsagen til dette er ikke, at der endnu ikke er fundet en generel lukket løsning. Det er snarere en grundlæggende, påviselig egenskab ved strukturen i differentialligningssystemet, der ikke tillader eksistensen af ​​en lukket løsning.
3. ↑ Som i Newtons tilfælde er eksistensen af ​​“integralerne”, dvs. H. af bevarede bevægelsesmængder, begrundet i den generelle Noether -sætning .
4. ↑ Da der ikke er nogen symmetrier, kan eksistensen af ​​bevarede mængder ikke udledes af den generelle Noether -sætning.

Individuelle beviser

1. ^ Isaac Newton: De matematiske fysiske principper. Oversat og redigeret af Volkmar Schüller, de Gruyter, Berlin (bl.a.) 1999, ISBN 3-11-016105-2 , (s. 184 ff., Forslag LVII til LXIII).
2. ↑ Ágoston Budó: Teoretisk mekanik . 4. udgave. VEB Deutscher Verlag der Wissenschaften, Berlin 1967, § 22, s. 104-108 . 
3. ^ Clifford M. Will : Teori og eksperiment i gravitationsfysik. Revideret udgave. Cambridge University Press, Cambridge et al. 1993, ISBN 0-521-43973-6 .
4. ^ Albert Einstein, Leopold Infeld : Om partikels bevægelse i generel relativitetsteori. I: Canadian Journal of Mathematics. Bind 1, 1949, s. 209-241, doi : 10.4153 / CJM-1949-020-8 .

litteratur

• Andreas Guthmann: Introduktion til himmelsk mekanik og ephemeris calculus. BI-Wissenschaftsverlag, Mannheim m.fl 1994, ISBN 3-411-17051-4 .
• Archie E. Roy: Orbital Motion. 3. udgave, elevtekst. Adam Hilger, Bristol et al. 1988, ISBN 0-85274-228-2 .
• Walter Thirring : Lærebog i matematisk fysik. Bind 1: Klassiske dynamiske systemer. 2., revideret udgave. Springer, Wien m.fl 1988, ISBN 3-211-82089-2 , (kapitel 4.2).
• Hannu Kartutunen, Pekka Kröger, Heikki Oja, Markku Poutannen, Karl J. Donner (red.): Fundamental Astronomy. Springer, Wien m.fl 1987, ISBN 3-540-17264-5 , (kap. 7).

Weblinks