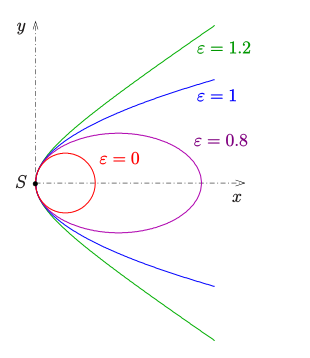
I plan geometri er en hyperbola en særlig kurve, der består af to symmetriske grene, der strækker sig ind i det uendelige. Ud over cirklen , parabolen og ellipsen er det en af de keglesnit, der opstår, når et plan skærer med en lige cirkelformet kegle .
Ligesom ellipser og paraboler kan hyperboler defineres som locus -kurver i planet (se afsnit Definition af en hyperbola som en locus -kurve ).
Hver hyperbola kan beskrives i et passende koordinatsystem ved hjælp af ligningen
(se afsnit Ligning ).

Hyperbola blev opdaget af Menaichmos . Navnet, der blev introduceret af Apollonios von Perge, stammer fra græsk og refererer til overdreven ( ὑπερβολή hyperbolé , fra oldgræsk βάλλειν bállein , tysk 'kast' , ὑπερβάλλειν hyperballein , tysk 'kast over målet' ) af den numeriske excentricitet (eller , se nedenfor) i det keglesnit: Når skæringsvinklen øges, bliver cirklen ( ) først til stadig mere langstrakte ellipser og derefter over parabolen ( og skæringsplanet er parallelt med et tangentielt plan af keglen) til hyperboler .



Definition af en hyperbola som et locus

Hyperbola: definition og asymptoter
En hyperbel er defineret som mængden af alle punkter på den plan den tegning , som mængden af den forskel mellem de afstande til to givne punkter, de såkaldte fokuspunkter og er konstant lig med :






Midten af fokuspunkterne kaldes centrum for hyperbola. Den lige linje, der forbinder fokuspunkterne, er hyperbolas hovedakse . På hovedaksen er de to hjørner i en afstand fra midten. Afstanden mellem fokuspunkterne og midtpunktet kaldes brændvidden eller lineær excentricitet og kaldes normalt som. Den dimensionsløse numeriske excentricitet, der er nævnt i indledningen, er .






Det faktum, at skæringspunktet mellem en lige cirkelformet kegle og et plan, der er stejlere end keglens overfladelinjer og ikke indeholder keglespidsen, er en hyperbola, vises ved at demonstrere ovenstående definerende egenskab ved hjælp af Dandelins sfærer (se afsnit Hyperbola som keglesnit ).

Hyperbola: definition med en guidecirkel
Bemærk:
Ligningen kan også tolkes som: Er cirklen med radius , så har bydelen samme afstand som omdrejningspunkt : Det kaldes at være forbundet Leitkreis af overdrivelse. Han skaber den rigtige gren











hyperbolen. Den venstre gren opnås analogt med guidecirklen, der tilhører brændpunktet .
Oprettelsen af en hyperbola med guidecirkler bør ikke forveksles med oprettelsen af en hyperbola med retningslinjer (se nedenfor ).



På grund af guidecirkelegenskaben er en gren af en hyperbola ækvidistancekurven til et af dens fokuspunkter og guidecirklen med det andet fokuspunkt som centrum.
Hyperbola i 1. hovedposition
ligning
Hyperbola -ligningen har en særlig enkel form, hvis den er i 1. hovedposition , det vil sige, at de to fokuspunkter på -aksen er symmetriske i forhold til oprindelsen; i tilfælde af en hyperbola i 1. hovedposition har fokuspunkterne koordinaterne og (med e = lineær excentricitet), og hjørnerne har koordinaterne
og .





For ethvert punkt i flyet er afstanden til brændpunktet den samme
og til det andet brændpunkt . Pointen ligger på hyperbolen, hvis og kun hvis forskellen mellem disse to udtryk er lige eller lige .







Ved algebraiske transformationer og med forkortelsen kan man vise, at ligningen


til ligningen

er ækvivalent. Sidstnævnte ligning kaldes hyperbolas ligning i 1. hovedposition.
Afsked
En hyperbola har kun to hjørner: og . I modsætning til ellipsen, her og er der ingen kurvepunkter. Sidstnævnte kaldes derfor også imaginære sekundære hjørner. Den lige linje gennem det lille toppunkt kaldes den mindre akse. Hyperbolen er symmetrisk i forhold til de store og mindre akser.




Asymptoter

Hyperbola: halvakser a, b, lin. Eccentricitet e, semi-parametre s
Hvis man løser hyperbola -ligningen for , opnår man


Her kan du se, at hyperbolen er knyttet til den lige linje
for størrelser, der er store

tilnærmelsesvis vilkårligt tæt. Disse lige linjer går gennem centrum og kaldes hyperbolas asymptoter
Halv parameter p
Halvdelen af længden af en hyperbolsen, der går gennem et brændpunkt og løber vinkelret på hovedaksen, kaldes den halve parameter (undertiden også den tværgående dimension eller bare parameter ) for hyperbolen. Han kan beregnes ved


Yderligere betydning af :

-
 er toppunktets krumningsradius,
er toppunktets krumningsradius,
d. Det vil sige, er radius af den cirkel gennem et toppunkt, der bedst passer til hyperbola i toppunktet. (Se nedenfor: Formelsamling / toppunktsligning .)

tangent
Den nemmeste måde at finde tangentens ligning i et hyperbolsk punkt er at implicit differentiere den hyperboliske ligning :



Under hensyntagen til :


Ligesidig hyperbola
En hyperbola, der gælder for, kaldes en ligesidet hyperbola. Deres asymptoter er vinkelret på hinanden. Den lineære excentricitet er den numeriske excentricitet og den halve parameter er .




Parametrisk display med hyperbolske funktioner
De hyperbolske funktioner resulterer i en parametrisk repræsentation af hyperbolen (analog til ellipsen) :



Hyperbola i 2. hovedposition
Hvis du bytter og , får du hyperboler i 2. hovedlag:


Hyperbola med en ligning y = A / x

Rotation af koordinatsystemet for at beskrive en ligesidet hyperbola som en graf over en funktion

3 ligesidede hyperboler med koordinatakserne som asymptoter røde: A = 1, magenta: A = 4; blå: A = 9

Hvis du roterer xy -koordinatsystemet rundt om vinklen og navngiver de nye koordinater , så er .
Den ligesidede hyperbola (semiaxerne er samme længde!) Har ligningen i de nye koordinater . Hvis du løser denne ligning for , får du






Så (i et xy -koordinatsystem) er grafen over funktionen med ligningen

-
 en ligesidet hyperbola med
en ligesidet hyperbola med
- koordinatakser som asymptoter,
- den lige linje som hovedaksen,

- den centrum og semi-akserne


- den afsked

- den halve parameter og radius af toppunktets krumning

- den lineære excentricitet og den numeriske excentricitet


- tangenten ved punktet


Ved at dreje den oprindelige hyperbola i rækkefølge (dette svarer til en rotation af koordinatsystemet til ), opnår man en ligesidet hyperbol med ligningen


-
 med
med
- De semi-akserne

- den lige linje som hovedaksen,

- den afsked

Hvis hyperbola forskydes med ligningen, så punktet er midten af den forskydede hyperbola, har den forskudte hyperbol ligningen



Den forskudte hyperbola har asymptoterne og .
Parametrene ændres ikke, når de flyttes.



Hyperbola som en keglesnit

Hyperbola (rød): elevation og sidehøjde af en kegle med Dandelins kugler d
1 , d
2
Hvis du skærer en lige cirkelformet kegle med et plan, hvis hældning er større end keglens hældning, og som ikke går gennem keglens spids, resulterer en hyperbola som en skæringskurve (se billede, rød kurve) . Beviset for den definerende egenskab med hensyn til fokuspunkterne (se ovenfor) udføres ved hjælp af to Dandelin -kugler , det er kugler, der berører keglen i cirkler eller og det hyperboliske plan i punkter eller . Det viser sig, at fokuspunkterne er skæringspunktets hyperbola.







-
 være ethvert punkt på skæringskurven.
være ethvert punkt på skæringskurven.
- Overfladelinjen gennemskærer cirklen i et punkt og cirklen i et punkt .





- Linjerne og er tangentielle til kuglen og er derfor af samme længde.



- Linjerne og er tangentielle til kuglen og er derfor af samme længde.



- Så er og derfor uafhængig af hyperbola -punktet .


Tangent som bisektor

Hyperbola: Tangent som halvdelen af fokalstrålerne
Følgende gælder for en hyperbola:
- Tangenten på et punkt er halvdelen af fokalstrålerne


Det følger heraf: En lysstråle, der udgår fra det ene fokuspunkt, reflekteres ved den hyperbolske tangens på en sådan måde, at det ser ud til at stamme fra det andet fokuspunkt.
- bevis
Til beviset bruger man hjælpepunktet på fokalstrålen , som har afstanden (se billede, er semiaxis af hyperbola). Den lige linje er halveringslinjen af fokalstrålerne. For at bevise, at tangenten er i punktet , viser man, at ethvert andet punkt fra ikke kan ligge på hyperbola. Så hyperbolen kan kun krydse på punktet og er derfor tangenten i . Fra tegningen kan det ses ( trekant ulighed ) det vil sige, dvs. h., det er . Hvis der var et hyperbolisk punkt, burde forskellen være den samme .


















Da en vinkeldisektor er let at tegne, tilbyder denne egenskab en enkel måde at konstruere tangenten i et hyperbolapunkt. Hvis de to asymptoter kendes i stedet for de to fokuspunkter, kan man bruge metoden beskrevet i afsnittet Tangent Construction .
Retningslinjer ejendom

Hyperbola: guideline property
Udtrykket directrix eller guideline betegner de to paralleller til minoraksen på afstand . For ethvert punkt på hyperbola er forholdet mellem afstandene til et brændpunkt og den tilhørende retningslinje lig med den numeriske excentricitet:



For at bevise det viser man det for og ligningen



er tilfreds.
Omvendt kan være et punkt (et fokuspunkt) og en lige linje (som en retningslinje) samt et reelt tal med specificere og definere en hyperbola som


- Sæt af alle punkter på flyet, for hvilke forholdet mellem afstandene til punktet og den lige linje er det samme .

Hvis du vælger , får du en parabel . For resultater i en ellipse .


For at bevise dette går man ud fra og betingelsen om, at der er et kurvepunkt. Retningslinjen er derefter beskrevet af ligningen . For følger af





-
 og herfra
og herfra 
Med forkortelsen får du


Dette er toppunktsligningen for en ellipse ( ), en parabel ( ) eller en hyperbola ( ). Se afsnittet Formelsamling .


Hvis man introducerer nye konstanter på en sådan måde, det vil
sige, så går toppunktsligningen ind




over. Dette er ligningen for en hyperbol med centrum og aksen som hovedaksen og semiaxer .



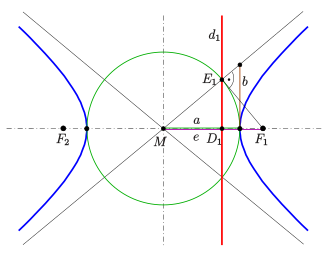
Konstruktion af retningslinjen

Konstruktion af en retningslinje:
På grund af dette er retningslinjens punkt (se billede) og fokuspunktet med hensyn til refleksionen ved den store vertexcirkel (grøn på billedet) inverse. Således som vist på billedet, kan du konstruere ved hjælp af den store knude cirkel : Pointen er skæringspunktet mellem toppunktet cirkel med Thales cirkel (ikke vist her) i løbet . Man beregner, at det også er på asymptoten. Så der er den videre konstruktion af som lodlinjen for lodlinjen fra til asymptoten (se billede). I sidste ende er retningslinjen vinkelret på hovedaksen.












Gevindkonstruktion af en hyperbola
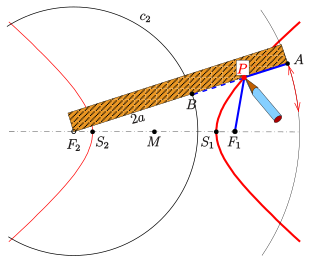
Hyperbola: gevindkonstruktion
Definitionen af en hyperbola ved hjælp af en guidecirkel ( se ovenfor ) giver en enkel mulighed for at tegne en hyperbolbue ved hjælp af en tråd og en lineal:
(0) Valg af fokuspunkter og afstanden mellem hjørnerne; radius af guide cirkel er også
(1) linealen er drejeligt fastgjort med den ene ende i venstre brændpunkt og punktet er markeret i en afstand på kanten
(2) gevind (blå) af længden
fastgørelse (3) af den ene ende af tråden ved punktet for linealen, den anden ende i brændpunktet
(4) Spænd tråden med en pen , således at den hviler mod kanten af linealen
(5) ved at dreje linealen omkring det punkt, den pen fejer hen over en hyperbolsk bue , fordi den er ( vejledende cirkelegenskab ).











Steiner generation af en hyperbola
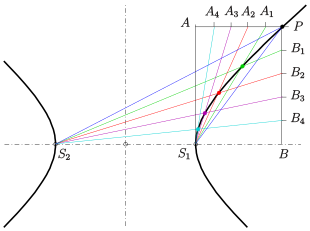
Hyperbola: Steiner -generation

Hyperbola y = 1 / x: Steiner -generation
Følgende idé om at konstruere individuelle punkter i en hyperbola er baseret på Steiners generation af en keglesnit (efter den schweiziske matematiker Jakob Steiner ):
- Hvis man har en projektiv, men ikke perspektivisk kortlægning af den ene tuft til den anden for to lige tuer på to punkter (alle lige linjer gennem punktet eller ) , danner skæringspunkterne for tildelte lige linjer et ikke-degenereret keglesnit.




Ved generering af individuelle punkter i hyperbola starter vi med de lige linie -tuer i hjørnerne . Vær nu et punkt med hyperbola og . Vi deler siden af rektanglet i n lige store stykker og overfører denne division til linjen ved hjælp af et parallelt projektion i diagonalsretningen (se billede). Den anvendte parallelle projektion giver den nødvendige projektive kortlægning af tuerne i og . Skæringspunkterne for de tildelte lige linjer og derefter ligge på hyperbola klart bestemt af specifikationerne.











Bemærk: Underinddelingerne kan fortsættes ud over punkterne eller for at konstruere yderligere punkter. Men da formaling af snit og en meget ujævn fordeling af punkter derefter forekommer, er det bedre at overføre konstruktionen af ovenstående punkter symmetrisk til de andre dele af hyperbola (se animation).


Kommentar:
- Steiner -generationen er også tilgængelig til ellipse og parabol . I det parabolske tilfælde kan påstanden let genberegnes.
- Steiner -generationen kaldes også parallelogrammetoden, for i stedet for hjørnerne kan der også bruges andre hyperbolske punkter på en hyperbolsk diameter. Derefter vises et parallelogram i stedet for et rektangel.
Hyperbola som et affint billede af den unitære hyperbola

Hyperbola som et affint billede af den unitære hyperbola
En anden definition af hyperbola bruger en særlig geometrisk kortlægning, nemlig affinitet . Her er hyperbola defineret som et affint billede af enhedens hyperbola .
hyperbola .
- Parametrisk repræsentation
En affin kortlægning i det virkelige plan har formen hvor er en regelmæssig matrix (determinant ikke 0) og er en vilkårlig vektor. Hvis søjlevektorerne er matrixen , bliver enhedshyperbola til hyperbola







afbilledet. er midtpunktet, et punkt for hyperbola og tangentvektor på dette tidspunkt. stå i. en. ikke vinkelret på hinanden. I. E. er jeg. A. Ikke toppunktet for hyperbolen. Men er asymptoternes retningsvektorer. Denne definition af en hyperbol giver en simpel parametrisk repræsentation af enhver hyperbola.






- Vertex, toppunktsform
Fordi i et toppunkt er tangenten til den tilhørende hyperbolske diameter vinkelret, og tangentretningen er i et hyperbolsk punkt

er, er parameteren for et toppunkt givet ved ligningen


og med det ude

til

Formlerne blev brugt.

Hvis er, og den parametriske repræsentation er allerede i toppunktsform.


De to knudepunkter i den hyperbel er
slutningen

og tilføjelsessætningerne for de hyperbolske funktioner resulterer i toppunktsformen af den parametriske repræsentation af hyperbolen:

- Eksempler

Hyperbola som en graf over funktionen y = 1 / x (eksempel 3)

Hyperbola: transformation til toppunktsform (eksempel 5)
-
 giver den sædvanlige parametriske repræsentation af hyperbola med ligningen
giver den sædvanlige parametriske repræsentation af hyperbola med ligningen 
-
 leverer den parametriske repræsentation af hyperbolen, der kommer ud af hyperbolen ved at dreje den i vinklen og derefter flytte den efter . Den parametriske repræsentation er allerede i toppunktsform. Det vil sige, er hyperbolas hjørner.
leverer den parametriske repræsentation af hyperbolen, der kommer ud af hyperbolen ved at dreje den i vinklen og derefter flytte den efter . Den parametriske repræsentation er allerede i toppunktsform. Det vil sige, er hyperbolas hjørner.



-
 giver hyperbola med ligningen Når man demonstrerer brug en
giver hyperbola med ligningen Når man demonstrerer brug en


- Hvis man skildrer hyperbolen med affine kortlægninger af formen , opnår man familien af alle hyperboler med asymptoter parallelt med aksen. Centret for en sådan hyperbola er specialiteten i denne hyperbolfamilie, at de kan repræsenteres som funktionsgrafer.




- Den parametriske repræsentation
-
 en hyperbola er ikke i form af et toppunkt.
en hyperbola er ikke i form af et toppunkt.
- Spidsparameteren resulterer fra til


- Spidsformen af det parametriske plot er:

- Afskeden er og

- halvaksen

- implicit repræsentation
Når vi løser den parametriske repræsentation ved hjælp af Cramers regel efter og brugt , opnår vi den implicitte repræsentation


-
 .
.
- Hyperbola i rummet
Hvis vektorerne er ude af , opnås en parametrisk repræsentation af en hyperbola i rummet.


Hyperbola som et affint billede af hyperbolen y = 1 / x
Da enhedshyperbola er ækvivalent med hyperbolen (se ovenfor), kan enhver hyperbole også forstås som et affint billede af hyperbolen :




 er centrum for hyperbola, der peger i retning af asymptoterne og er et punkt for hyperbola.
er centrum for hyperbola, der peger i retning af asymptoterne og er et punkt for hyperbola.


For tangentvektorresultaterne

I et toppunkt er tangenten til den tilhørende hyperbolske diameter vinkelret, dvs. h., det er

Så er vertex -parameteren
![t_0 = \ pm \ sqrt [4] {\ frac {\ vec f_2 ^ 2} {\ vec f_1 ^ 2}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b26de698fecd55664d5a6833e97148678656143)
For er og er hyperbolas hjørner.



Tangent konstruktion

Tangentkonstruktion: Asymptoter og P givet → tangent
Tangentvektoren kan skrives sådan ved at regne ud:


Det betyder, at i parallelogrammet er diagonalen parallel med tangenten i hyperbolapunktet (se billede). Denne egenskab giver en let måde at konstruere tangenten på et hyperbolsk punkt.



Bemærk: Denne egenskab ved en hyperbola er en affin version af 3-punkts degeneration af Pascals sætning .
Punktkonstruktion

Punktkonstruktion: Asymptoter og P
1 givet → P
2
En anden egenskab ved en hyperbola tillader konstruktion af hyperbolapunkter, hvis asymptoterne og et punkt for hyperbola er kendt:
For en hyperbola med den parametriske repræsentation (centerpunktet blev for enkelthedens skyld antaget at være nulpunktet):

Hvis der er to hyperbolske punkter, så ligger punkterne


på en lige linje gennem midtpunktet (se billede). Det enkle bevis følger af .

Bemærk: Denne egenskab ved en hyperbola er en affin version af 4-punkts degeneration af Pascals sætning .
Tangent-asymptote trekant

Hyperbola: tangent-asymptote trekant
Af de følgende overvejelser antager vi for enkelthedens skyld, at midten er ved oprindelsen (0,0), og at vektorerne har samme længde. Hvis sidstnævnte ikke er tilfældet, sættes den parametriske repræsentation først i toppunktsform (se ovenfor). Som et resultat er hjørnerne og de mindre hjørner . Så er og .





Hvis tangentens skæringspunkter i det hyperbolske punkt med asymptoterne beregnes, opnås de to punkter


Arealet af trekanten kan udtrykkes ved hjælp af en 2 × 2 determinant:


Se beregningsregler for determinanter .
er diamantens område, der spænder over. Arealet af en diamant er lig med halvdelen af det diagonale produkt. Diagonalerne i denne diamant er halvakser . Så:



- Det område af trekanten er uafhængig af hyperbel punkt


Affinere selvbilleder af hyperbolen y = 1 / x
Ikke hver affin kortlægning af det virkelige affineplan (se forrige afsnit) kortlægger hyperbolen til en anden hyperbola. Følgende affine kortlægninger forlader hyperbola -invarianten som helhed:




Særlige tilfælde:
- For hvert punkt i flyet forbliver fast. Dette billede kaldes identitet.

- For hvert punkt i hyperbolen flyttes, dvs. dvs. der er ikke noget fast punkt på hyperbolaen.

- For figuren er punktrefleksionen ved nulpunktet.

- For figuren er den "normale" refleksion på den lige linje .


- For figuren er den skrå refleksion på den lige linje i retning af den lige linje . (Se afsnittet Centers of Parallel Chords .)



Centre for parallelle sener

Hyperbola: Centrene for parallelle sener ligger på en lige linje.

Hyperbola: En senes midtpunkt halverer også asymptotessenen.
Følgende gælder for hver hyperbola:
- Centrene for parallelle sener (se billede) ligger på en lige linje gennem hyperbolas centrum.
Dette betyder, at der for hvert par punkter i en akkord er en skrå refleksion på en lige linje gennem midten af hyperbola, som bytter punkterne og kortlægger hyperbolen til sig selv. En skrå refleksion forstås som en generalisering af en normal refleksion på en lige linje , hvor alle punkter-til-billede punkter er parallelle med hinanden, men ikke nødvendigvis vinkelret på spejlaksen .





Den nemmeste måde at bevise denne egenskab på hyperbola . Da alle hyperboler er affinebilleder af enhedshyperbola og dermed også af hyperbolen og, i tilfælde af en affin kortlægning, passerer linjecentre ind i billedlinjernes centre, gælder ovenstående egenskab for alle hyperboler.


Bemærk:
Senens punkter kan også ligge på forskellige grene af hyperbolen.

En konsekvens af denne symmetri er: Asymptoterne i hyperbolen udskiftes i den skrå refleksion og midtpunktet for en hyperbolsk akkord halverer også den tilhørende afstand mellem asymptoterne, dvs. det vil sige, det gælder . Denne egenskab kan bruges til at konstruere et vilkårligt antal yderligere hyperboliske punkter for kendte asymptoter og et punkt ved at bruge det respektive segment til at konstruere .








Hvis akkorden degenererer til en tangent, skærer kontaktpunktet sektionen mellem asymptoterne.

Pol-polært forhold
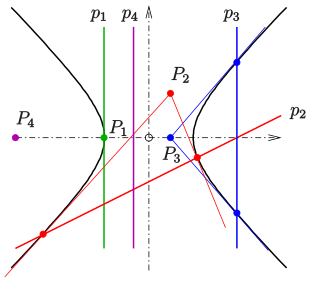
Hyperbola: pol-polært forhold
En hyperbola kan altid beskrives i et passende koordinatsystem ved en ligning af formen . Tangentens ligning i et hyperbolsk punkt er
Hvis man tillader i denne ligning, at ethvert punkt i planet, der er forskelligt fra nulpunktet, er, så tildeles den rette linje til punktet . Denne lige linje går ikke gennem midten af hyperbolen.






Du kan gøre omvendt
- den lige linje punktet eller


- den lige linje punktet


tildele. Et sådant tildelingspunkt ↔ lige linje kaldes en polaritet eller et pol-polært forhold . Den pol er det punkt, den polære er den tilsvarende lige linje.
Betydningen af dette pol-polære forhold er, at de mulige skæringspunkter mellem polar af et punkt med hyperbola er kontaktpunkterne for tangenterne gennem polen til hyperbolen.
- Hvis punktet (polen) ligger på hyperbolen, er dens polar tangent på dette tidspunkt (se billede :) .

- Hvis polen ligger uden for hyperbolen, er skæringspunkterne mellem polar og hyperbola kontaktpunkterne for tangenterne gennem polen til hyperbolen (se billede :) .

- Hvis punktet ligger inden for hyperbola, har dets polar ikke noget skæringspunkt med hyperbola (se billede :) .

Til bevis: Bestemmelse af skæringspunktet mellem polar for et punkt med hyperbola og søgning efter hyperboliske punkter, hvis tangenter indeholder punktet, fører til det samme ligningssystem.



Bemærkninger:
- Skæringspunktet mellem to polarer (f.eks. På billedet :) er polen på den lige linje, der forbinder de tilhørende poler (her :) .


- Omdrejningspunktet eller og retningslinjen eller er polære i forhold til hinanden.




- Lige linjer gennem midten af hyperbolen har ingen poler. De siger: "Dine poler er på langdistancen lige ."
- Midten af hyperbola har ingen polar, "det er den fjerne lige linje".
- Pol-polære forhold findes også for ellipser og paraboler . Se også projektivt keglesnit .
Ortogonale tangenter

Hyperbola med ortoptisk kurve (lilla)
For en hyperbol ligger skæringspunkterne for ortogonale tangenter på cirklen . (I tilfælde er der ingen ortogonale tangenter.)



Denne cirkel kaldes den ortoptiske kurve for den givne hyperbola.
Hyperboler af formen y = a / (x - b) + c
Perifer vinkel indstillet til hyperboler
Hyperbolas i formen er funktionsgrafer, der er entydigt bestemt af de tre parametre . Så du har brug for tre punkter for at bestemme disse parametre. En hurtig metode er baseret på den perifere vinkel, der er indstillet for hyperboler.



Hyperbola: sæt perifere vinkler
En vinkel, der skal måles mellem to akkorder, bærer vi to linjer, der hverken er for - eller aksen er parallel, en firkantet :


- For to lige linjer måler vi den tilsvarende vinkel med tallet .


To lige linjer er parallelle, og derfor er vinkeldimensionen lig med 1.

Analogt med sættet med perifere vinkler til cirkler gælder det her
Perifert vinkelsæt (til hyperboler):
- For fire punkter (se billede) gælder følgende:

- De fire punkter ligger kun på en hyperbol af formen, hvis vinklerne ved og i ovenstående vinkelmål er ens, dvs. dvs. hvis:




(Bevis ved genberegning. Man kan for en retning antage, at punkterne ligger på en hyperbola y = a / x.)
3-punkts form af en hyperbola
Analogt med 2-punktsformen af en lige linje (gradientvinkler måles med gradienten), resulterer sættet af perifere vinkler for hyperboler i
3-punkts form (for hyperboler):
- Hyperbolas ligning gennem tre punkter opnås ved at løse ligningen


- efter y.
Formelsamling
Hyperbolisk ligning
En hyperbol med et center (0 | 0) og akse som hovedakse opfylder ligningen


Asymptoterne for den tilhørende hyperbola er de lige linjer:

Fokuspunkter er:

En hyperbol med et center og den lige linje som hovedaksen opfylder ligningen



Enhver hyperbol, hvis asymptoter er de lige linjer med ligningerne, har en ligning af formen


F.eks .: Hvis asymptoterne er koordinatakser , skyldes alle hyperboler en ligning .


Vertex ligning
Familien af hyperboler, hvis akse er -aksen, et toppunkt er punktet (0,0) og midten (-a, 0) kan udtrykkes ved ligningen


beskrive.
Følgende gælder for hyperboler . Indsæt denne ligning

-
 så du får en cirkel,
så du får en cirkel,
- for en ellipse,

- til en lignelse.

Med den samme halve parameter har de keglesnit alle den samme krumningsradius ved toppunktet S:

Parametriske repræsentationer
for hyperbolen med ligningen :

1: 
2: 
3: (repræsentation med rationelle funktioner).

4: Tangenthældning som parameter:
En parameter, der viser tangent hældningen anvendes i den respektive Hyperbelpunkt, opnås analogt med tilfældet med ellipse , ved der ved udskiftning og formler anvendes til de hyperbolske funktioner:




Her er den øvre og den nederste halvdel af hyperbolen. Punkterne med lodrette tangenter (hjørner ) er ikke omfattet af denne parametriske fremstilling.



Tangentens ligning ved punktet er


Denne ligning er et vigtigt redskab til at bestemme den ortoptiske kurve for et hyperbola.
I polære koordinater

Hyperbola: polar repræsentation, pol = center

Hyperbola: polær repræsentation, pol = fokuspunkt
Bemærk
- i det første tilfælde (pol er midten af hyperbola), at radicand kan blive negativ. Der er ingen hyperboliske punkter for sådanne vinkler.
- I det andet tilfælde (pol er et fokuspunkt for hyperbola) er der to hyperboliske punkter (på grund af ) på hver stråle, for hvilken nævneren ikke er 0 . For de to hjørner resultat.


Vinkel på hovedaksen, pol i midten (0,0):

Vinkel på hovedaksen, pol i et fokuspunkt (se keglesnit ):

Tangentligning
Midtpunkt (0 | 0), hovedakse som akse, kontaktpunkt


Midtpunkt , hovedakse parallel med aksen, kontaktpunkt



Krumningsradius
Krumningsradius for hyperbola i de to hjørner er


-
 (som en ellipse i de vigtigste hjørner).
(som en ellipse i de vigtigste hjørner).
Hyperbola som trisectrix
Allerede i det 4. århundrede brugte Pappos fra Alexandria denne egenskab ved hyperbola som et ekstra hjælpemiddel til at løse problemet med at dele en vinkel i tre dele. Det er bevist, at der ikke er nogen løsning, hvis du begrænser dig til "euklidiske værktøjer", kompasser og linealer .
Metoden beskrevet nedenfor er i vid udstrækning taget fra essayet om vinklenes trisektion af K. Matter (1902). I konstruktionen vist deri vinkel toppunkt, i modsætning til at ifølge Pappos , ikke ligger på ordinaten af hyperblens. Forudsat for forskellige vinkelområder altid den samme akkordlængde, så kan det bare med en konstrueret hyperbole vinkelområder fra omtrent til at lukke så tidligt som når tilstrækkelig plads opdeles i tredjedele. Navnene på hyperbola er blevet tilpasset den nuværende standard.






Skitse til foreløbig behandling
Som en foreløbig betragtning z. B. før en vinkel som en del af en cirkulær sektor , hvor punkt skiller den bue i forhold . A optages deri trekant med senen opnået således ifølge cirkel vinkel sæt ved toppunktet af vinklen og i spidsen af vinklen er toppunktet af koordinatoprindelse af kartesiske koordinatsystem , gælder det punkt den - koordinat ( interval )














- (1)

Afskaffelse af den
- Transformér ligningsbetingelser (1)
- (2)

- (3) er en dobbeltvinkelfunktion , derfor også gældende

- (4)

- (2) indsæt i (4)
- (5)

- Læg (5) og (3), quasi eliminere

- (6)

- holder således for

- (7)

endelig får du hyperbola -ligningen

Dette resulterer i designrelevante funktioner, der også gælder uden brug af det kartesiske koordinatsystem , dvs. H. en specifik retning eller position af senen er ikke påkrævet:

- det midterste punkt er på senen

- halvaksen

- den excentricitet

- venstre hyperbelastning løber gennem toppunktet (i det følgende benævnt toppunkt ).



Animation af trisektionen af vinklen ved hjælp af hyperbola
Den egentlige konstruktion begynder med placeringen af det vinklede toppunkt og indtegningen af de to vinklede ben, som omslutter enhver vinkelbredde af vinklen . Derefter tegnes en bue rundt med en frit valgbar radius ; det første fokuspunkt og det andet toppunkt i det senere hyperbola resultat ved de vinklede ben. Der følger en lige linje gennem punkter og den afstand er næsten den sene efter senen tredjedele af i og afstanden er fra lige linje plottet på, vil det være klart for den ønskede hyperbel det andet brændpunkt og















- Halvakse og

- excentricitet

Nu hyperbola ved hjælp af toppunktets fokuspunkter samt z. B. tegnet ved hjælp af en dynamisk geometri -software (DGS) eller en mekanisk hyperbolsk cirkel.



Den rigtige gren af hyperblen skærer den bue og giver den konklusion, skal den kun en halv linje startende ved




Hyperboler som plane sektioner af kvadriker
Følgende andenordens overflader ( quadrics ) har hyperboler som plane sektioner:
Hyperbola y = 1 / x over et vilkårligt talfelt
Hvis man overvejer det sæt, der opfylder den hyperboliske ligning i et affinisk plan over et hvilket som helst (kommutativt) legeme , forbliver mange egenskaber ved det virkelige tilfælde, som er formuleret med "skærer", "forbinder" og "parallelt", og hvis bevis kun er multiplikation / Brug division og addition / subtraktion. F.eks .:


- En lige linie skærer hyperbel i højst to punkter.

- Gennem hver Hyperbelpunkt der bortset aksen parallelt linjer ligefrem en lige linje med den hyperbel kun punkt til fælles, at tangenten : . En lige linje uden et skæringspunkt kaldes en forbipasserende , og en lige linie med to punkter i krydset kaldes en sekant .




Forskelle i den virkelige sag:
- For (rationelle tal) er den lige linje en forbipasserende, fordi ligningen ikke har nogen løsning.




- Der er ingen forbipasserende for (komplekse tal). F.eks .: skærer hyperbola i punkterne .



- Hvis kroppen har karakteristik 2 (dvs. 1 + 1 = 0), er der ingen sekanter blandt de lige linjer , da hver ligning i tilfælde af karakteristik 2 højst har en løsning (der er ikke noget ” ”). Tangenten ved det hyperbolske punkt (for karakteristik 2) har ligningen . Det betyder, at alle tangenter går gennem nulpunktet (0,0).





Se også
Hændelse
litteratur
- Peter Proff: Fortolkningen af udtrykkene "ellipse", "parabel" og "hyperbola" ifølge Apollonios v. Perge. I: “gelêrter der arzeniê, ouch apotêker”. Bidrag til videnskabens historie. Festschrift til Willem F. Daems 70 -års fødselsdag. Redigeret af Gundolf Keil , Horst Wellm Verlag, Pattensen / Hannover 1982 (= Würzburg medicinhistorisk forskning, 24), ISBN 3-921456-35-5 , s. 17–34.
Weblinks
Individuelle beviser
-
^ IN Bronstein, KA Semendjajew (grundlægger), Günter Grosche (arrangement), Eberhard Zeidler (red.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6 , s.24 .
-
^ Frans van Schooten : Mathematische Oeffeningen , Leyden, 1659, s. 327
-
↑ a b Erich Hartmann: Projektiv geometri. (PDF; 180 kB). Kort manuskript, TU Darmstadt, s. 12-16.
-
^ Jacob Steiners foredrag om syntetisk geometri. BG Teubner, Leipzig 1867. Del 2, s. 96. ( begrænset forhåndsvisning i Google bogsøgning)
-
↑ Forelæsningsnotat Planar Circle Geometries, en introduktion til Moebius-, Laguerre- og Minkowski Planes (PDF; 757 kB) s. 33.
-
↑ Forelæsningsnotat Planar cirkelgeometrier , en introduktion til Moebius-, Laguerre- og Minkowski-fly (PDF; 757 kB) s.32 .
-
↑ a b Regina Bruischütz: 5. kantede trisektion med hyperboler (ifølge Pappus ca. 300 e.Kr.). I: Vinkeldeling i tre dele - konstruktion med ekstra værktøj (del A). University of Bayreuth, 26. maj 1997, s. 3 , åbnet den 22. juli 2019 .
-
^ Robert C. Yates: TRISEKTIONSPROBLEMET, 3. Hyperbola. I: ERIC. National Council of Teachers of Mathematics, Inc., Washington, DC, 1971, s. 32-33 , åbnede 27. juli 2019 .
-
↑ K. Matter: Til vinklenes tredeling. I: e-perodica. ETH Zürich, 1902, s. 20-23 , åbnet den 22. juli 2019 .
-
↑ CDKG: Computerstøttet deskriptiv og konstruktiv geometri. (PDF; 3,4 MB) TU Darmstadt, s.108.
-
↑ CDKG: Computerstøttet deskriptiv og konstruktiv geometri. (PDF; 3,4 MB) TU Darmstadt, s.118.
-
↑ CDKG: Computer-Aided Descriptive and Constructive Geometry. (PDF; 3,4 MB) TU Darmstadt, s. 123.










































































































































































































![t_0 = \ pm \ sqrt [4] {\ frac {\ vec f_2 ^ 2} {\ vec f_1 ^ 2}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b26de698fecd55664d5a6833e97148678656143)