Keglesnit

Keglesnit:
( 1 ) giver parabolen, ( 2 ) cirkel og ellipse, ( 3 ) hyperbolen

Et keglesnit (Latin sectio conica , engelsk keglesnit ) er en kurve , der oprettes, når overfladen af en dobbelt kegle skæres med et plan . Hvis skæreplanet indeholder spidsen af ​​keglen, oprettes enten et punkt eller en lige linje eller et skærende par lige linjer som snittet . Hvis punktet ikke er inkluderet, opstår de ikke-degenererede koniske sektioner ellipse , cirkel (en særlig form for ellipsen), parabel eller hyperbola .

Beviset for, at i ikke det degenererede tilfælde disse kurver, der er defineret som locuskurver i planet, virkelig opstår, kan udføres uden beregning ved hjælp af Dandelins kugler . Beregningsbeviset er givet her i afsnittet Plansektioner i enhedskeglen.

Et keglesnit kan også ses som et todimensionalt specialtilfælde af et kvadratisk og kan beskrives ved en ligning af 2. grad, den generelle keglesnitligning .

Hvis man indlejrer ellipsen, hyperbolen og parabolen i et projektivt plan, opstår der projicerende keglesnit, som alle er ækvivalente med hinanden, dvs. Det vil sige, de kan konverteres til hinanden ved hjælp af lineære billeder.

Ellipse: definition

Parabel: definition

Hyperbola: definition

Degenererede keglesnit:
skærende parpar, parallelle parpar, en lige linje, et punkt

Ligninger af koniske sektioner

Koniske sektioner kan beskrives i et passende xy-koordinatsystem ved ligninger af 2. grad:

• Ellipse med centrum M ved punktet (0,0) og hovedaksen på x-aksen:

  ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} + {\ frac {y ^ {2}} {b ^ {2}}} = 1, \ quad b = | MS_ { 3} |, \ qquad a, b \ neq 0 \ quad,}$(se billede). (For er en cirkel.)${\ displaystyle a = b = r}$

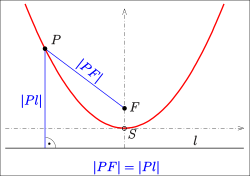
• Parabel med toppunkt ved punkt (0,0) og aksen på y-aksen:

  ${\ displaystyle y = ax ^ {2}, \ quad a = {\ frac {1} {4 | SF |}}, \ qquad a \ neq 0 \ quad,}$ (se billede).

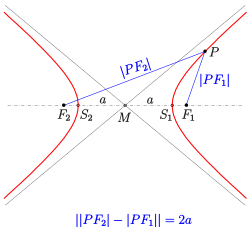
• Hyperbola med centrum M ved punktet (0,0) og hovedaksen på x-aksen:

  ${\ displaystyle {\ frac {x ^ {2}} {a ^ {2}}} - {\ frac {y ^ {2}} {b ^ {2}}} = 1, \ quad b ^ {2} = | MF_ {1} | ^ {2} -a ^ {2}, \ qquad a, b \ neq 0 \ quad,}$ (se billede).

• For at blive skåret lige par med skæringspunktet på det punkt (0,0):

  ${\ displaystyle a ^ {2} x ^ {2} -y ^ {2} = 0, \ a \ neq 0.}$

• Lige gennem punktet (0,0):

  ${\ displaystyle x ^ {2} = 0.}$

• Punkt, punktet (0,0):

  ${\ displaystyle a ^ {2} x ^ {2} + b ^ {2} y ^ {2} = 0, \ a, b \ neq 0.}$

Af hensyn til fuldstændigheden tilføjes yderligere to tilfælde, der faktisk ikke vises som keglesnit, men som også er beskrevet af ligninger af 2. grad:

• Parallelt par linjer:

  ${\ displaystyle x ^ {2} = a ^ {2}, \ a \ neq 0.}$

• Det tomme sæt:

  ${\ displaystyle x ^ {2} + y ^ {2} = - 1}$eller .${\ displaystyle x ^ {2} = - 1}$

De sidste to tilfælde kan vises som plane sektioner af en lige cirkulær cylinder . En cirkulær cylinder kan forstås som et begrænsende tilfælde af en kegle med en kegle-spids ved uendelig. Derfor tager du disse to sager med til koniske sektioner.

Flade sektioner af enhedens kegle

Koniske sager

For at bestemme, at de kurver / punkter, der er omtalt ovenfor som koniske sektioner, faktisk opstår, når en kegle krydser et plan, skærer vi her enhedskeglen (lige cirkulær kegle ) med et plan, der er parallelt med y-aksen. Dette er ikke en begrænsning, da keglen er rotationssymmetrisk. Enhver lige cirkulær kegle er det affine billede af enhedskeglen og ellipser / hyperboler / paraboler / ... smelter sammen i det samme i et affinalt billede . ${\ displaystyle K_ {1} \ colon x ^ {2} + y ^ {2} = z ^ {2}}$${\ displaystyle K_ {1}}$

Givet: flykegle . ${\ displaystyle \ varepsilon \ colon ax + cz = d \,}$${\ displaystyle K_ {1} \ colon x ^ {2} + y ^ {2} = z ^ {2}}$

Ønsket: skåret . ${\ displaystyle \ varepsilon \ cap K_ {1}}$

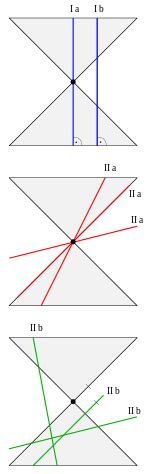
• Tilfælde I: I dette tilfælde er flyet vinkelret og og . Hvis man eliminerer fra kegleligningen, opnår man . ${\ displaystyle c = 0}$${\ displaystyle a \ neq 0}$${\ displaystyle x = d / a}$${\ displaystyle x}$${\ displaystyle z ^ {2} -y ^ {2} = d ^ {2} / a ^ {2}}$
  • Sag Ia . I dette tilfælde består sektionen af
  parret med linjer .${\ displaystyle d = 0}$ ${\ displaystyle t (0,1, \ pm 1), \ t \ in \ mathbb {R}.}$
• Sag Ib . Ovenstående ligning beskriver nu en hyperbol i yz-planet. Så selve skæringskurven er også en hyperbola.${\ displaystyle d \ neq 0}$${\ displaystyle \ varepsilon \ cap K_ {1}}$

Sag II: . Hvis man eliminerer fra konusligningen ved hjælp af planligningen , opnår man ligningssystemet${\ displaystyle c \ neq 0}$${\ displaystyle z}$${\ displaystyle (1) \ quad (c ^ {2} -a ^ {2}) x ^ {2} + 2adx + c ^ {2} y ^ {2} = d ^ {2}, \ qquad (2 ) \ quad ax + cz = d.}$

• Case IIa: For det

plan passerer gennem toppunktet og ligning (1) nu har form . ${\ displaystyle d = 0}$ ${\ displaystyle (0,0,0)}$${\ displaystyle (c ^ {2} -a ^ {2}) x ^ {2} + c ^ {2} y ^ {2} = 0}$

For klippet er

pointen .${\ displaystyle c ^ {2}> a ^ {2}}$ ${\ displaystyle P_ {0} = (0,0,0)}$

For snittet er den

lige linje${\ displaystyle c ^ {2} = a ^ {2}}$ ${\ displaystyle t (c, 0, -a), \ t \ in \ mathbb {R}.}$

For snittet er parret med linjer${\ displaystyle c ^ {2} <a ^ {2}}$ ${\ displaystyle t (c / \ pm {\ sqrt {a ^ {2} -c ^ {2}}}, 1, -a / \ pm {\ sqrt {a ^ {2} -c ^ {2}} }), \ t \ in \ mathbb {R}.}$

Sag IIb: For det flyet ikke går gennem det punkt af keglen og er ikke vinkelret.${\ displaystyle d \ neq 0}$

For (1) bliver til, og skæringskurven er en parabel.${\ displaystyle c ^ {2} = a ^ {2}}$${\ displaystyle x = - {\ frac {c ^ {2}} {2ad}} y ^ {2} + {\ frac {d} {2a}}}$

For vi forvandler (1) til .${\ displaystyle c ^ {2} \ neq a ^ {2}}$${\ displaystyle {\ frac {(c ^ {2} -a ^ {2}) ^ {2}} {d ^ {2} c ^ {2}}} \ venstre (x + {\ frac {ad} {c ^ {2} -a ^ {2}}} \ højre) ^ {2} + {\ frac {c ^ {2} -a ^ {2}} {d ^ {2}}} y ^ {2} = 1}$

For krydset er kurven en ellipse og${\ displaystyle c ^ {2}> a ^ {2}}$

for der er en hyperbola.${\ displaystyle c ^ {2} <a ^ {2}}$

Parameterrepræsentationer af krydsningskurverne kan findes i Weblink CDKG, s. 106-107.

Resumé:

• Hvis skæreplanet ikke indeholder toppen af ​​keglen , oprettes de ikke-degenererede keglesnit (se billede til Ib, IIb), nemlig en parabel, en ellipse eller en hyperbol, afhængigt af om kegleaksen fra skæreplanet er under den samme, en større eller en mindre Vinklen skæres som ved keglens generatrix.
• Hvis keglespidsen på den anden side ligger i skæreplanet, oprettes degenererede keglesnit (se figur for la, IIa), nemlig et punkt (nemlig toppen af ​​keglen), en lige linje (nemlig en overfladelinie) eller et krydsende par lige linjer (nemlig to overfladelinjer) .

Generel konisk ligning

Den generelle ligning for keglesnit er

${\ displaystyle ax ^ {2} + bxy + cy ^ {2} + dx + ey + f = 0}$

(bemærk, at parametrene a og b ikke er dem i det foregående afsnit)

Specielt er parametrene ikke alle 0. Hvis det er, beskriver ligningen en lige linje eller en helhed . ${\ displaystyle a, b, c}$${\ displaystyle a = b = c = 0}$${\ displaystyle \ mathbb {R} ^ {2}}$

Ellipse: transformation af større akse

Det skal nu vises, at kun de ovennævnte 8 tilfælde forekommer som opløsningssæt i den generelle keglesnitligning. Vi opnår målet i to vigtige trin, omdannelsen af ​​hovedaksen :

1. Rotation af koordinatsystemet for at fjerne udtrykket .${\ displaystyle xy}$
2. Skift af nulpunktet (oversættelse), så de lineære termer forsvinder så langt som muligt .${\ displaystyle \ prikker x + \ prikker y}$

1. trin: I så fald udfører vi rotation${\ displaystyle b \ neq 0}$

${\ displaystyle (x, y) = (x '\ cos \ alpha -y' \ sin \ alpha, x '\ sin \ alpha + y' \ cos \ alpha)}$

rundt om vinklen med eller , hvis , igennem.${\ displaystyle \ alpha}$${\ displaystyle \ tan (2 \ alpha) = {\ tfrac {b} {ac}}}$${\ displaystyle \ alpha = 45 ^ {\ circ}}$${\ displaystyle a = c}$

Ligningssnittligningen har derefter formen

${\ displaystyle Ax ^ {2} + By ^ {2} + Cx + Dy + E = 0,}$(i stedet for at blive brugt igen ).${\ displaystyle x ', y'}$${\ displaystyle x, y}$

2. trin:

Hvis er en førende, der udfylder firkanten til udtrykket og dermed skifter .${\ displaystyle A \ neq 0}$${\ displaystyle A \ left (x + {\ tfrac {C} {2A}} \ right) ^ {2}}$ ${\ displaystyle x '= x + {\ tfrac {C} {2A}}}$

Hvis er et kvadratisk supplement fører til udtrykket og dermed til at skifte .${\ displaystyle B \ neq 0}$${\ displaystyle B \ left (y + {\ tfrac {D} {2B}} \ right) ^ {2}}$ ${\ displaystyle y '= y + {\ tfrac {D} {2B}}}$

Efter disse to trin har konisk sektionsligning (x 'og y' igen erstattet af x, y) endelig formen

I: med eller${\ displaystyle ux ^ {2} + vy ^ {2} + w = ​​0}$${\ displaystyle u, v \ neq 0}$

II: eller med .${\ displaystyle ux ^ {2} + vy + w = ​​0}$${\ displaystyle uy ^ {2} + vx + w = ​​0}$${\ displaystyle u \ neq 0}$

Kun ovenstående otte tilfælde kan forekomme:

I tilfælde af I er der en ellipse eller en hyperbola eller det tomme sæt, hvis det er, eller et punkt eller et skærende par linjer, hvis det er.${\ displaystyle w \ neq 0}$${\ displaystyle w = 0}$

I tilfælde II resulterer en parabel, hvis den er, eller et parallelt par par, eller en lige linje eller det tomme sæt, hvis det er.${\ displaystyle v \ neq 0}$${\ displaystyle v = 0}$

Transformationerne udført her (rotation, forskydning) ændrer ikke den geometriske form af den koniske sektion beskrevet af den oprindelige ligning. Parametre såsom semi-akser for ellipser og hyperbola eller brændvidde for parabolen eller vinkel / afstand mellem skærende / parallelle lige linjer kan aflæses fra den transformerede koniske sektion.

Bemærk: Den kvadratiske del af den generelle koniske sektionsligning kan også skrives ved hjælp af en 2 × 2 matrix :

${\ displaystyle {\ begin {pmatrix} x & y \ end {pmatrix}} {\ begin {pmatrix} a & b / 2 \\ b / 2 & c \ end {pmatrix}} {\ begin {pmatrix} x \\ y \ end {pmatrix }} + dx + ey + f = 0.}$

Da en rotation og et skift ikke ændrer tegnet på determinanten for 2 × 2-matrixen, fører til sag I og tilfælde II. Hvis du ved, at den oprindelige koniske sektionsligning repræsenterer en konisk sektion, der ikke er degenereret, kan du allerede se fra determinanten om det er en ellipse ( ) eller en hyperbola ( ) eller en parabel ( ). ${\ displaystyle \ delta = ac - {\ tfrac {b ^ {2}} {4}}}$${\ displaystyle \ delta \ neq 0}$${\ displaystyle \ delta = 0}$${\ displaystyle \ delta}$${\ displaystyle \ delta> 0}$${\ displaystyle \ delta <0}$${\ displaystyle \ delta = 0}$

Kommentar:

• Da den generelle keglesnitligning kun bestemmes af de 6 koefficienter op til en faktor, kræves 5 point (ligninger) for at bestemme koefficienterne . Men: Ikke hvert valg af 5 point definerer klart en konisk sektion. (Modeksempel: 4 punkter på en lige linje, 1 punkt ikke på den lige linje.) Et ikke-degenereret keglesnit (ellipse, hyperbola, parabola) er tydeligt defineret med 5 punkter uden nr. 3 på en lige linje. En elegant formel til den uudviklede sag bruger en 6 × 6 determinant :

  ${\ displaystyle {\ begin {vmatrix} x ^ {2} & xy & y ^ {2} & x & y & 1 \\ x_ {1} ^ {2} & x_ {1} y_ {1} & y_ {1} ^ {2} & x_ {1} & y_ {1} & 1 \\ x_ {2} ^ {2} & x_ {2} y_ {2} & y_ {2} ^ {2} & x_ {2} & y_ {2} & 1 \\ x_ {3} ^ {2} & x_ {3} y_ {3} & y_ {3} ^ {2} & x_ {3} & y_ {3} & 1 \\ x_ {4} ^ {2} & x_ {4} y_ {4} & y_ {4} ^ {2 } & x_ {4} & y_ {4} & 1 \\ x_ {5} ^ {2} & x_ {5} y_ {5} & y_ {5} ^ {2} & x_ {5} & y_ {5} & 1 \\\ slutning { vmatrix}} = 0 \ quad,}$( er de givne punkter. Se.)${\ displaystyle (x_ {i}, y_ {i}), i = 1, \ prikker, 5}$

• En cirkel er tydeligt defineret med 3 punkter (ikke på en lige linje). Ligningen fås fra 4 × 4 determinanten

  ${\ displaystyle {\ begin {vmatrix} x ^ {2} + y ^ {2} & x & y & 1 \\ x_ {1} ^ {2} + y_ {1} ^ {2} & x_ {1} & y_ {1} & 1 \ \ x_ {2} ^ {2} + y_ {2} ^ {2} & x_ {2} & y_ {2} & 1 \\ x_ {3} ^ {2} + y_ {3} ^ {2} & x_ {3} & y_ {3} & 1 \\\ slut {vmatrix}} = 0}$.

Eksempel: Keglesnittet i de 5 punkter er ovenfor ifølge beregning af determinantligning eller efter forenkling . Transformationen af ​​hovedaksen finder sted med en rotation på . Et skift er ikke nødvendigt. Den koniske sektion har den transformerede ligning og er en ellipse. ${\ displaystyle (1,0), (- 1,0), (0,1), (- 1, -1), (1,1)}$${\ displaystyle -4x ^ {2} + 4xy-4y ^ {2} + 4 = 0}$${\ displaystyle x ^ {2} -xy + y ^ {2} -1 = 0}$${\ displaystyle 45 ^ {\ circ}}$${\ displaystyle {\ tfrac {x ^ {2}} {2}} + {\ tfrac {3} {2}} y ^ {2} -1 = 0}$

Vertex ligning af en familie af koniske

Keglesnitssæt: p fast, variabel${\ displaystyle \ varepsilon}$

Familien af ​​ikke-degenererede keglesnit, hvis akse er -aksien, og som har et toppunkt ved punktet (0,0), kan gives ved ligningen ${\ displaystyle x}$

• ${\ displaystyle y ^ {2} = 2px + (\ varepsilon ^ {2} -1) x ^ {2} \ qquad, \ p> 0 \, \ varepsilon \ geq 0}$

beskrive (for beviser se retningslinjeegenskab for hyperbolen ). Til

${\ displaystyle \ varepsilon = 0}$du får en cirkel,

for en ellipse,${\ displaystyle 0 <\ varepsilon <1}$

til en parabel og${\ displaystyle \ varepsilon = 1}$

for en hyperbola.${\ displaystyle \ varepsilon> 1}$

${\ displaystyle \ varepsilon}$er den numeriske excentricitet.

${\ displaystyle 2p}$ er bredden af ​​den koniske sektion målt ved brændpunktet vinkelret på aksen.

${\ displaystyle p}$er toppunktets krumningsradius i toppunktet .${\ displaystyle (0,0)}$

For ellipser og hyperboler , hvor er den semi-store akse og den lineære excentricitet . I tilfælde af en ellipse, den center er og et omdrejningspunkt. I tilfælde af en hyperbel, dette er den centrum og et omdrejningspunkt. I tilfælde af en parabel, at fokus er. For cirklen (med ) er midtpunktet, og radius er .${\ displaystyle \ varepsilon = e / a}$${\ displaystyle a}$${\ displaystyle e}$${\ displaystyle (a, 0)}$${\ displaystyle (ae, 0)}$${\ displaystyle (-a, 0)}$${\ displaystyle (ea, 0)}$${\ displaystyle ({\ tfrac {p} {2}}, 0)}$${\ displaystyle \ varepsilon = 0}$${\ displaystyle (p, 0)}$${\ displaystyle p}$

Polarligning af en familie af koniske

Konisk sektion: til at definere retningslinjer

Familie med keglesnit med fælles fokus i polære koordinater

Den vejledende egenskab af ikke-degenererede keglesnit er:

• Sættet med punkter i det euklidiske plan, hvis afstande fra en given lige linje og et givet punkt, der opfylder betingelsen, er konstant, er en ellipse, hvis , en parabel, hvis en hyperbol, hvis den er.${\ displaystyle l}$${\ displaystyle F}$${\ displaystyle {\ frac {| PF |} {| Pl |}} = \ varepsilon> 0}$${\ displaystyle 0 <\ varepsilon <1}$${\ displaystyle \ varepsilon = 1}$${\ displaystyle \ varepsilon> 1}$

Hvis punktet er nulpunktet, og den lige linje har ligningen , gælder følgende i polære koordinater (se figur): ${\ displaystyle F}$${\ displaystyle l}$${\ displaystyle x = -d}$

${\ displaystyle {\ frac {| PF |} {| Pl |}} = {\ frac {r} {r \ cos \ varphi + d}} = \ varepsilon \.}$

Løs først for leveringer . Hvis man indstiller , opnår man den polære repræsentation af de ikke-degenererede koniske sektioner: ${\ displaystyle r}$${\ displaystyle r = {\ frac {\ varepsilon d} {1- \ varepsilon \ cos \ varphi}}}$${\ displaystyle p = r (\ pi / 2) = \ varepsilon d}$

• ${\ displaystyle r = {\ frac {p} {1- \ varepsilon \ cos \ varphi}}}$.

${\ displaystyle p}$er halvparameteren (halv bredde af keglesnittet i brændpunktet) og den numeriske excentricitet. Hvis du vælger den faste halvparameter, får du keglesnit med nulpunktet som det fælles fokuspunkt, nemlig ${\ displaystyle \ varepsilon}$${\ displaystyle p}$

for den cirkel med centrum og radius ,${\ displaystyle \ varepsilon = 0}$${\ displaystyle M = (0,0)}$${\ displaystyle R = p}$

for den ellipse med midtpunktet og semi-akser ,${\ displaystyle 0 <\ varepsilon <1}$${\ displaystyle M = (e, 0), \ e = {\ frac {p \; \ varepsilon} {1- \ varepsilon ^ {2}}}}$${\ displaystyle a = {\ frac {e} {\ varepsilon}}, \ b = {\ sqrt {a ^ {2} -e ^ {2}}}}$

for den parabel med toppunktet og ligningen ,${\ displaystyle \ varepsilon = 1}$${\ displaystyle S = (- {\ frac {p} {2}}, 0)}$${\ displaystyle x = {\ frac {y ^ {2} -p ^ {2}} {2p}}}$

for den hyperbel med centrum og semi-akserne .${\ displaystyle \ varepsilon> 1}$${\ displaystyle M = (- e, 0), \ e = {\ frac {p \; \ varepsilon} {\ varepsilon ^ {2} -1}}}$${\ displaystyle a = {\ frac {e} {\ varepsilon}}, \ b = {\ sqrt {e ^ {2} -a ^ {2}}}}$

Keglesnitstubber

Hvis ligningerne af to koniske sektioner er angivet, er den lineære kombination ${\ displaystyle f_ {1} (x, y) = 0, \ f_ {2} (x, y) = 0}$

• ${\ displaystyle a_ {1} f_ {1} (x, y) + a_ {2} f_ {2} (x, y) = 0}$

af ligningerne genererer nye koniske sektioner. Da proportionale par og ækvivalente ligninger resulterer og derfor hører til samme keglesnit, skrives den lineære kombination ofte som: ${\ displaystyle (a_ {1}, a_ {2})}$${\ displaystyle (ta_ {1}, ta_ {2})}$

• ${\ displaystyle (1- \ mu) f_ {1} (x, y) - \ mu f_ {2} (x, y) = 0}$

Cirkelbuffer til to givne cirkler (rød)

Keglesnitsknuder med 3 lige linjer (rød: cirkel for , magenta: ellipse, blå: parabel til , grøn: hyperbola)${\ displaystyle \ mu = {\ tfrac {5} {9}}}$${\ displaystyle \ mu = {\ tfrac {1} {5}}}$

Conic sektion tuft gennem 4 point

Denne ligning beskriver utvetydigt et keglesnit gennem parameteren . ${\ displaystyle \ mu}$

Eksempel på cirkulære knopper:

For de to cirkulære ligninger

${\ displaystyle f_ {1} (x, y) = (x-2) ^ {2} + y ^ {2} -1 = 0}$

${\ displaystyle f_ {2} (x, y) = (x + 2) ^ {2} + y ^ {2} -1 = 0}$

beskriver med en klynge af cirkler (se billede). (I de kvadratiske termer annulleres hinanden, og den lige linje resulterer .) ${\ displaystyle (1- \ mu) f_ {1} (x, y) - \ mu f_ {2} (x, y) = 0}$${\ displaystyle \ mu \ neq 1/2}$${\ displaystyle \ mu = 1/2}$${\ displaystyle x = 0}$

Eksempel på en konisk sektion gennem 2 punkter med specificerede tangenter:

Følgende eksempel bygger en klynge af keglesnit fra 3 lige linjer . Lad det være: ${\ displaystyle g_ {1}, g_ {2}, g_ {3}}$

${\ displaystyle g_ {0}: f_ {0} (x, y) = y = 0}$

${\ displaystyle g_ {1}: f_ {1} (x, y) = y / 2-x-1 = 0}$

${\ displaystyle g_ {2}: f_ {2} (x, y) = y / 2 + x-1 = 0}$

Beskriv derefter ligningen

${\ displaystyle (1- \ mu) f_ {1} (x, y) \ cdot f_ {2} (x, y) - \ mu f_ {0} (x, y) ^ {2} = 0}$

med familieparameteren en klynge af keglesnit gennem de to punkter og . Hvert keglesnit berører de to lige linjer på disse punkter. Keglesnitstubben bestemmes således af de to punkter og de to tangenser på disse punkter. ( Et keglesnit er altid klart defineret af 5 specifikationer!) Begge kegler, som den lineære kombination dannes med, er degenererede kegler ( er et par lige linjer og er en dobbelt lige linje ). ${\ displaystyle \ mu}$${\ displaystyle P_ {1} = g_ {0} \ cap g_ {1}}$${\ displaystyle P_ {2} = g_ {0} \ cap g_ {2}}$${\ displaystyle g_ {1}, g_ {2}}$${\ displaystyle P_ {1}, P_ {2}}$${\ displaystyle g_ {1}, g_ {2}}$${\ displaystyle f_ {1} f_ {2} = 0}$${\ displaystyle f_ {0} ^ {2} = 0}$

Eksempel på en konisk sektion gennem 4 punkter:

I dette tilfælde er tuften en lineær kombination af to parallelle parpar, der krydser hinanden ved de 4 punkter (se billede): ${\ displaystyle (\ pm 1, \ pm 1)}$

${\ displaystyle a_ {1} (x ^ {2} -1) + a_ {2} (y ^ {2} -1) = 0}$

Præcis en (muligvis degenereret) konisk sektion af tuften går gennem hvert punkt i planet, der er forskelligt fra tuftens basispunkter. F.eks. Opnås nulpunktet for linjeparret . ${\ displaystyle (0,0)}$${\ displaystyle a_ {1} = 1, a_ {2} = - 1}$${\ displaystyle y ^ {2} = x ^ {2}}$

Keglesnitsknuder studeres grundigt i litteraturen.

Ækvivalens af ikke-degenererede keglesnit

• Alle ellipser er affine billeder af enhedens cirkel (se ellips ).
• Alle paraboler er affine billeder af den normale parabel (se parabel ).
• Alle hyperboler er affine billeder af enhedshyperbola (se hyperbola ).

Imidlertid kan en ellipse ikke (f.eks.) Kortlægges på en parabel med en affin kortlægning . Hvis imidlertid affinakoordinatplanet føjes til et projektivt plan, og det fjerne punkt på dets akse føjes til en parabel, kan en ellipse med en projektiv kortlægning kortlægges på en sådan udvidet parabel. Det samme gælder for en hyperbol suppleret med de to fjerne punkter i dens asymptoter.

• Fra det projektive synspunkt er alle ikke-degenererede projicerende koniske sektioner ækvivalente med hinanden (se også CDKG-weblink, s. 251).

Eksempler:

1. Den projektive kortlægning med kortlægger enhedens cirkel på parabolen .${\ displaystyle (x, y) \ to ({\ tfrac {x} {1 + y}}, {\ tfrac {1-y} {1 + y}})}$${\ displaystyle x ^ {2} + y ^ {2} = 1}$${\ displaystyle y = x ^ {2}}$
2. Den projektive kortlægning med kortlægger parabolen på hyperbolen .${\ displaystyle (x, y) \ to ({\ tfrac {1} {x}}, {\ tfrac {y} {x}})}$${\ displaystyle y = x ^ {2}}$${\ displaystyle y = {\ tfrac {1} {x}}}$

Anvendelser og eksempler

Koniske sektioner beskriver banerne for himmellegemer

Konisk sektion i arkitektur: Brasilia-katedralen

De keglesnit anvendes i astronomi , da banerne for de himmellegemer er tilnærmede keglesnit.

De bruges også i optik - som en ellipsoid af revolution for billygter , som en paraboloid eller hyperboloid til spejlteleskoper osv.

I beskrivende geometri vises koniske sektioner som billeder af cirkler i parallelle og centrale fremspring. Se Ellipse (beskrivende geometri) .

historie

Den græske matematiker Menaichmos undersøgte keglesnittene på Platons akademi ved hjælp af en keglemodel . Han fandt ud af, at Delian-problemet kan spores tilbage til bestemmelsen af ​​skæringspunktet mellem to koniske sektioner. Derefter behandlede Aristaios fra Samos (Aristaios den ældre) problemet med konstruktionen af ​​koniske sektioner i forhold til tre eller fire lige linjer i en ikke længere eksisterende bog, som senere blev taget op igen i begrundelsen for den analytiske geometri af René Descartes . Euclid skrev fire bøger om keglesnit, men de har ikke overlevet for os. Apollonios von Perge opsummerede al den viden, som de gamle matematikere havde om keglesnittene, i sit otte bind arbejde Konika , hvor Apollonios som Euclid foretrak den syntetiske tilgang til geometri. Værkerne fra Euclid, Apollonios og Aristaios blev taget op og videreudviklet i Vesteuropa fra renæssancen og fremefter. Beskrivelsen af ​​keglesnit ved hjælp af koordinatligninger blev introduceret af Fermat og Descartes.

Koniske sektioner over et hvilket som helst antal felter

Koniske sektioner kan også defineres over alle kroppe . Et overraskende antal forekomster og symmetriegenskaber bevares. Se weblinket Projective Geometry, Projective Conics og for Conics over begrænsede kroppe artiklen Quadratic Set .

Konik og Benz-fly

Koniske sektioner spiller en vigtig rolle i Benz-flyene , som er Möbius-planer (geometri af cirklerne), Laguerre-planer (geometri af paraboler) og Minkowski-planer (geometri af hyperboler).

Se også

• Koniske sektioner som rationelle Bezier-kurver
• Konfokale koniske sektioner
• Fokus konisk sektion
• Kurvbue , himmelsk mekanik , to-kropsproblem , projektiv geometri , rotationskvadrisk , samling af formler til analytisk geometri .

Weblinks

Wiktionary: konisk sektion  - forklaringer på betydninger, ordets oprindelse, synonymer, oversættelser

• Keglesnit. ( Memento af 5. marts 2016 i internetarkivet ). Universitetet i Wien.
• Projektiv geometri. Kort script. Darmstadt University (PDF; 180 kB), s. 12–16.
• Computerstøttet udførelse og konstruktiv geometri. (CDKG) Universitet i Darmstadt (PDF; 3,4 MB).
• Apollonius von Pergas syv bøger om keglesnit.
• J. Casey: En afhandling om den analytiske geometri af punkt-, linie-, cirkel- og keglesnit. 1893.
• A. Coffman: Linear Systems of Conics.

litteratur

• Max Koecher , Aloys Krieg : niveau geometri. 3. udgave, Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3 .
• Burg, Haf, Wille: Højere matematik for ingeniører. Bind II, Teubner-Verlag Stuttgart, ISBN 3-519-22956-0 , s.338 .

støttende dokumenter

1. ↑ Lille encyklopædi for matematik. VEB Verlag Enzyklopädie, Leipzig, 1977, s. 325 f.
2. ^ Meyberg & Vachenauer: Højere matematik 1. Springer-Verlag, Berlin, ISBN 3-540-59188-5 , s. 309.
3. ↑ For eksempel Barry Spain: Analytical Conics. Dover Publications, 2007, ISBN 0-486-45773-7 , s.91 .
4. ↑ Projektiv geometri. Kort script, Uni Darmstadt (PDF; 180 kB), s. 12.