Analytisk geometri

Den analytiske geometri (også vektorgeometri ) er en gren af geometrien , de algebraiske værktøjer (især fra lineær algebra ) giver mulighed for at løse geometriske problemer. I mange tilfælde gør det det muligt at løse geometriske opgaver rent aritmetisk uden at bruge visualisering som hjælp.

I modsætning hertil kaldes geometri, der etablerer sine sætninger på et aksiomatisk grundlag uden henvisning til et talesystem, syntetisk geometri .

Metoderne til analytisk geometri anvendes i alle naturvidenskaber , men frem for alt i fysik , såsom beskrivelsen af planetbaner . Oprindeligt behandlede analytisk geometri kun spørgsmål om plan og rumlig ( euklidisk ) geometri. I den generelle forstand beskriver analytisk geometri imidlertid affine rum med vilkårlige dimensioner over vilkårlige kroppe .

Koordinatsystemet

Et koordinatsystem er et afgørende hjælpemiddel i analytisk geometri. I praksis anvendes normalt et kartesisk koordinatsystem . For nogle enkle spørgsmål, såsom bestemmelse af lige linjekryds, undersøgelse af lige linjer for parallelisme eller beregning af delvise forhold , ville et skråt koordinatsystem være tilstrækkeligt. Et kartesisk koordinatsystem er uundværligt, hvis der skal beregnes afstande eller vinkler .

Vektorer

Mange beregninger af analytisk geometri er standardiseret og forenklet ved hjælp af metoderne til vektorberegning. Selvom al analytisk geometri blev opfundet uden vektorer og selvfølgelig stadig kan praktiseres uden vektorer, og omvendt kan vektorrum defineres som en abstrakt-algebraisk konstruktion uden geometrisk reference, synes brugen af ​​vektorer i kartesiske koordinatsystemer så naturlig, at “ Lineær algebra og analytisk geometri ”i gymnasiet og i de matematiske-fysisk-tekniske bachelorstudier generelt som et kursus.

Koordinering og parameterligninger

Mere komplekse geometriske strukturer såsom lige linjer , planer , cirkler , sfærer forstås som sæt af punkter og beskrevet af ligninger . Disse kan være koordinatligninger eller parametriske ligninger.

Implicit koordinatligning

Et beregningsudtryk, der afhænger af koordinaterne , indstilles til 0.${\ displaystyle (x, y, \ dotsc)}$

Eksempel (lige linje i tegningsplanet)

${\ displaystyle 2x-3y + 7 = 0}$

Eksplicit koordinatligning

Et af koordinaterne udtrykkes af det andet.

Eksempel (niveau i rummet)

${\ displaystyle z = 2x-5y + 3}$

Eksplicit koordinatligninger har den ulempe, at der ofte skal sondres mellem sager; sådan er det f.eks

i flyet umuligt at vise en parallel til -aksen i formen .${\ displaystyle y}$${\ displaystyle y = mx + t}$

Parametrisk ligning

Positionen vektor for ethvert punkt i konstruktionen er givet ved en vektor aritmetisk udtryk, der indeholder en eller flere parametre.${\ displaystyle {\ vec {x}} = {\ overrightarrow {OX}}}$${\ displaystyle X}$

Eksempel (lige i rummet): ${\ displaystyle {\ vec {x}} = {\ begin {pmatrix} 2 \\ - 4 \\ - 3 \ end {pmatrix}} + \ lambda {\ begin {pmatrix} -2 \\ 0 \\ 5 \ slut {pmatrix}}}$

Flyets analytiske geometri

Peger i flyet

Hvert punkt i planet er beskrevet af to koordinater , f.eks. B .. Koordinaterne kaldes normalt (i denne rækkefølge) -koordinaten (også: abscissa ) og -koordinaten (også: ordinat ). Udtrykkene og bruges også . ${\ displaystyle P}$${\ displaystyle P (2 \ mid -1 {,} 5)}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$

De samlede koordinater for punkter danner ordnede par i den flade sag .

Lige linjer i flyet

Koordinatligning (implicit)

${\ displaystyle n_ {x} x + n_ {y} y + n_ {0} = \, \! 0}$

Man taler også om den normale (en) form af ligelinjen, da vektoren er vinkelret på den lige linje.${\ displaystyle {\ begin {pmatrix} n_ {x} \\ n_ {y} \ end {pmatrix}}}$

Parametrisk ligning

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}}}$

Her er placeringsvektoren for ethvert vilkårligt, men fast punkt på den lige linje (støttepunkt); er en såkaldt retningsvektor , dvs. en vektor, hvis retning er parallel med den lige linje.${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$${\ displaystyle {\ vec {u}}}$

Anden ordens kurver i flyet

Ved en (implicit koordinat) ligning af anden grad

${\ displaystyle Ax ^ {2} + By ^ {2} + Cxy + Dx + Ey + F = 0}$

en keglesnit er generelt angivet. Afhængig af koefficienternes værdier kan det være en ellipse (specielt tilfælde: cirkel ), en parabel eller en hyperbola .

Analytisk geometri i det euklidiske rum

Punkter i rummet

Hvert punkt i rummet bestemmes af tre koordinater , f.eks. B .. Hvert punkt er tildelt sin position vektor , som er forbindelsen vektor mellem oprindelsen af koordinatsystemet og givet punkt. Dens koordinater svarer til punktets , men er skrevet som en søjlevektor: ${\ displaystyle P}$${\ displaystyle P = P (4 \ mid -0 {,} 5 \ mid -3)}$${\ displaystyle P}$ ${\ displaystyle {\ overrightarrow {OP}}}$${\ displaystyle P}$

${\ displaystyle {\ overrightarrow {OP}} = {\ begin {pmatrix} 4 \\ - 0 {,} 5 \\ - 3 \ end {pmatrix}}}$

Koordinaterne kaldes -, - og -koordinater eller -, - og -koordinater (i den rækkefølge) . ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle x_ {3}}$

De samlede koordinater for punkter danner 3-tupler i det rumlige tilfælde .

Lige linjer i rummet

Koordinere ligninger

Lige linjer i rummet kan ikke beskrives af en enkelt koordinatligning. En lige linje kan altid forstås som skæringspunktet (skæringspunktet) mellem to planer og koordinatligninger af disse to planer (se nedenfor) kan bruges til klart at definere den lige linje.

Parametrisk ligning

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}}}$

Så ligningen har samme form som i det to-dimensionelle tilfælde.

Niveauer i rummet

Koordinatligning (implicit)

${\ displaystyle n_ {x} x + n_ {y} y + n_ {z} z + n_ {0} = \, \! 0}$

Denne type planligning kaldes normal form , da vektoren er vinkelret (normal) på planet.${\ displaystyle {\ vec {n}} = {\ begynder {pmatrix} n_ {x} \\ n_ {y} \\ n_ {z} \ end {pmatrix}}}$

Parametrisk ligning

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda {\ vec {u}} + \ mu {\ vec {v}}}$

${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$er positionsvektoren for ethvert vilkårligt, men fast punkt på planet (støttepunkt); og er lineært uafhængige retning vektorer (eller span vektorer ), dvs. vektorer parallelt med planet, at "span" planet.${\ displaystyle {\ vec {u}}}$${\ displaystyle {\ vec {v}}}$

Anden ordens overflader i rummet

Anden graders generelle koordinatligning

${\ displaystyle Ax ^ {2} + By ^ {2} + Cz ^ {2} + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0}$

beskriver en overflade af anden orden . De vigtigste specielle tilfælde er:

Ellipsoid , elliptisk paraboloid , hyperbolsk paraboloid , single-shell hyperboloid , dobbelt-shell hyperboloid , kegle , elliptisk cylinder , parabolisk cylinder , hyperbolsk cylinder .

Generalisering: Analytisk geometri af ethvert affineret rum

Begreberne analytisk geometri kan generaliseres ved at tillade koordinater fra enhver krop og alle dimensioner .

Hvis der er et vektorrum over et legeme og et tilknyttet affint rum , kan et -dimensionelt underrum af beskrives ved hjælp af parameterligningen ${\ displaystyle V}$${\ displaystyle K}$${\ displaystyle R}$${\ displaystyle V}$${\ displaystyle k}$${\ displaystyle R}$

${\ displaystyle {\ overrightarrow {OX}} = {\ overrightarrow {OA}} + \ lambda _ {1} {\ vec {v_ {1}}} + \ dotsb + \ lambda _ {k} {\ vec {v_ {k}}}}$.

Her er placeringsvektoren for ethvert vilkårligt, men fast punkt i underområdet (supportpunkt); vektorerne er lineært uafhængige vektorer, som er en basis af underrum af hvilken vederlaget underrum tilhører. ${\ displaystyle {\ overrightarrow {OA}} = {\ vec {A}}}$${\ displaystyle {\ vec {v_ {1}}}, \ dotsc, {\ vec {v_ {k}}}}$${\ displaystyle V}$${\ displaystyle R}$

For er ligningen af ​​en lige linje for ligningen af ​​et plan. Hvis 1 er mindre end dimensionen af eller , taler man om et hyperplan . ${\ displaystyle k = 1}$${\ displaystyle k = 2}$${\ displaystyle k}$${\ displaystyle R}$${\ displaystyle V}$

I analogi med andenordens kurver (koniske sektioner) af plangeometri og andenordens overflader af rumlig geometri betragtes såkaldte kvadrater også i -dimensionalt affinrum , det vil sige andenordens overflader (med dimensionen ) , som er skabt af anden grad koordinat ligninger er defineret: ${\ displaystyle n}$${\ displaystyle n-1}$

${\ displaystyle \ sum _ {i = 1} ^ {n} \ sum _ {j = 1} ^ {n} A_ {ij} x_ {i} x_ {j} + \ sum _ {i = 1} ^ { n} B_ {i} x_ {i} + C = 0}$

Typiske opgaver i analytisk geometri

Forekomst gennemgang

Målet her er at bestemme, om et givet punkt tilhører et givet sæt punkter (f.eks. Til en lige linje).

I to-dimensionelt rum

Som et eksempel, den lige linje med den eksplicitte koordinatligning

${\ displaystyle y = 2 \ cdot x-3}$

skal ses som.

Punktet ligger på denne lige linje, som det kan ses ved at indsætte koordinaterne og (punktprøven): ${\ displaystyle P (2 | 1)}$${\ displaystyle x = 2}$${\ displaystyle y = 1}$

${\ displaystyle 1 = 2 \ cdot 2-3}$

Pointen er dog ikke på den lige linje. For og er nemlig ${\ displaystyle S (4 | 2)}$${\ displaystyle x = 4}$${\ displaystyle y = 2}$

${\ displaystyle 2 \ neq 2 \ cdot 4-3}$.

I et tredimensionelt rum

Det skal kontrolleres, om punktet ligger på den lige linje med følgende parameterform : ${\ displaystyle Q (-1 \ mid 9 \ mid -2)}$

${\ displaystyle {\ vec {x}} = {\ begin {pmatrix} -7 \\ 7 \\ - 6 \ end {pmatrix}} + t {\ begin {pmatrix} 3 \\ 1 \\ 2 \ end { pmatrix}}}$ .

Hvis positionen vektor af der anvendes, fører til følgende 3 ligninger: ${\ displaystyle {\ vec {x}}}$${\ displaystyle {\ overrightarrow {OQ}}}$${\ displaystyle Q}$

${\ displaystyle {\ begin {matrix} -1 & = & - 7 & + & t \ cdot 3 & \ Rightarrow & t = 2 \\ 9 & = & 7 & + & t \ cdot 1 & \ Rightarrow & t = 2 \\ - 2 & = & - 6 & + & t \ cdot 2 & \ Rightarrow & t = 2 \\\ slut {matrix}}}$

Siden har den samme værdi i alle tre tilfælde (her ), ligger på den lige linje. ${\ displaystyle t}$${\ displaystyle 2}$${\ displaystyle Q}$

Bestemmelse af skæringspunktet mellem to sæt punkter

Bestemmelse af skæringspunktet mellem to sæt punkter (fx skæringspunktet mellem to lige linjer) svarer til at løse et ligningssystem . Afhængigt af hvilken form de to sæt punkter er beskrevet, varierer proceduren lidt:

sag 1

Begge sæt punkter er givet ved koordinatligninger .

I dette tilfælde er krydset beskrevet af totaliteten af ​​koordinatligningerne.

Sag 2

Begge sæt punkter er givet ved hjælp af parameterligninger .

Skæringspunktet opnås ved at ligne de højre sider af disse ligninger.

Sag 3

Et af punktsætene er givet af en koordinatligning , det andet af en parametrisk ligning.

I dette tilfælde indsættes de enkelte koordinater for vektorparameterligningen i vektorligningen.

I to-dimensionelt rum

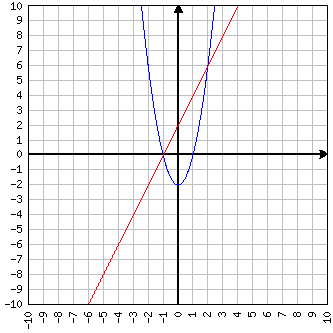
Det skal kontrolleres, om og hvor graferne over funktionerne og skærer hinanden. Og svarer til : ${\ displaystyle g (x)}$${\ displaystyle f (x)}$${\ displaystyle g (x) = 2x ^ {2} -2}$${\ displaystyle f (x) = 2x + 2}$

For at beregne skæringspunkterne er funktionsbetingelserne for ligningerne for de to funktioner nu sat ens. På denne måde finder man koordinaterne, for hvilke de to funktioner har samme koordinat: ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ begin {matrix} 2x ^ {2} & - & 2 & = & 2 \ cdot x & + & 2 \\ 2x ^ {2} & - & 2 \ cdot x & - & 4 & = & 0 \\ x ^ {2} & - & x & - & 2 & = & 0 \\\ slut {matrix}}}$

Løsning af denne kvadratiske funktion fører til løsningerne: og . ${\ displaystyle x_ {1} = - 1}$${\ displaystyle x_ {2} = 2}$

Hvis du udskifter det til en af ​​de to indledende ligninger, får du skæringspunkterne ved: og . ${\ displaystyle S_ {1} (- 1 | 0)}$${\ displaystyle S_ {2} (2 | 6)}$

I et tredimensionelt rum

Det bør kontrolleres, om og på hvilket tidspunkt de to rette linjer og krydser hinanden. De to lige linjer er defineret som følger: ${\ displaystyle g_ {1}}$${\ displaystyle g_ {2}}$

${\ displaystyle g_ {1}: \; {\ vec {x}} = {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ end {pmatrix}} + s \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ end {pmatrix}} \ qquad \ left (s \ in \ mathbb {R} \ right)}$

${\ displaystyle g_ {2}: \; {\ vec {x}} = {\ begin {pmatrix} -2480 \\ 105 \\ 1167 \\\ slutning {pmatrix}} + t \ cdot {\ begin {pmatrix} 150 \\ 120 \\ 1 \\\ ende {pmatrix}} \ qquad \ venstre (t \ i \ mathbb {R} \ højre)}$

Som i et todimensionelt rum sidestilles de to ligninger også her:

${\ displaystyle {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ end {pmatrix}} + s \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ slut {pmatrix }} = {\ begin {pmatrix} -2480 \\ 105 \\ 1167 \\\ ende {pmatrix}} + t \ cdot {\ begin {pmatrix} 150 \\ 120 \\ 1 \\\ slutning {pmatrix}} }$

${\ displaystyle s \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ slut {pmatrix}} - t \ cdot {\ begin {pmatrix} -150 \\ - 120 \\ - 1 \ \\ end {pmatrix}} = {\ begin {pmatrix} -2500 \\ 135 \\ - 33 \\\ end {pmatrix}}}$

Vektorligningen kan opdeles i følgende 3 ligninger:

${\ displaystyle {\ begin {array} {ccccl | l} -100 \ gange s & - & 150 \ gange t & = & - 2500 & \ gange 3/50 \\ 225 \ gange s & - & 120 \ gange t & = & 135 &: 5 \\ -3 \ cdot s & - & 1 \ cdot t & = & - 33 & \ cdot (-2) \\\ end {array}} \ Leftrightarrow {\ begin {array} { ccccl} -6 \ cdot s & - & 9 \ cdot t & = & -150 \\ 45 \ cdot s & - & 24 \ cdot t & = & 27 \\ 6 \ cdot s & + & 2 \ cdot t & = & 66 \\\ slut {array}}}$

Tilføjelse af det første og sidste ligningsudbytte eller . Fra den første ligning resulterer således ved at anvende det . Denne løsning opfylder også den anden ligning, fordi . ${\ displaystyle -7 \ cdot t = -84}$${\ displaystyle t = 12}$${\ displaystyle -6 \ cdot s = -42}$${\ displaystyle s = 7}$${\ displaystyle 45 \ times 7-24 \ times 12 = 27}$

Positionsvektoren for skæringspunktet mellem de lige linjer opnås ved at indsætte en af ​​de to beregnede parametre ( ) i den tilsvarende lige linje ( ): ${\ displaystyle s}$${\ displaystyle g_ {1}}$

${\ displaystyle {\ begin {pmatrix} 20 \\ - 30 \\ 1200 \\\ end {pmatrix}} + 7 \ cdot {\ begin {pmatrix} -100 \\ 225 \\ - 3 \\\ end {pmatrix }} = {\ begin {pmatrix} -680 \\ 1545 \\ 1179 \\\ slutning {pmatrix}} \ Rightarrow S \ venstre (-680 | 1545 | 1179 \ højre)}$

historie

Analytisk geometri blev grundlagt af den franske matematiker og filosof René Descartes . Større forbedringer skyldes Leonhard Euler , der især behandlede kurverne og overfladerne i anden orden. Udviklingen af ​​vektorberegning (af blandt andet Hermann Graßmann ) gjorde vektornotationen almindelig i dag mulig.

David Hilbert har bevist, at tredimensionel analytisk geometri svarer fuldstændigt til (syntetisk) euklidisk geometri i den form, han specificerede . Rent praktisk er det langt bedre end dette. I den første halvdel af det tyvende århundrede blev det derfor opfattet, at geometri på den måde, som den er blevet undervist siden Euklid, kun var af historisk interesse.

Nicolas Bourbaki gik endda et skridt videre: han undlod helt geometriske begreber som punkt, lige linje osv. Og betragtede alt nødvendigt for at være blevet sagt med behandlingen af lineær algebra . Som altid med Bourbaki ignoreres naturligvis anvendelsen af anvendt matematik fuldstændigt.

Se også

• Dynamisk rumlig geometri
• Analytisk geometri formel samling
• Lige linje ligning
• Planligning
• Cirkulær ligning
• Subtangent

litteratur

• Gerd Fischer : Analytisk geometri: En introduktion til nye studerende . Vieweg, 2001
• Wilhelm Blaschke : Analytisk geometri . Springer, 1953

Weblinks

• Ina Kersten : Analytisk geometri og lineær algebra . Script, University of Göttingen
• Joachim Gräter: Analytisk geometri . Script, University of Potsdam
• A. Fyldstof: Analytisk geometri på Spektrum.de