vektor

I generel forstand i lineær algebra er en vektor ( lat. Vektor "bærer, driver") et element i et vektorrum , det vil sige et objekt, der kan tilføjes til andre vektorer og ganges med tal kaldet skalarer . Vektorer i denne generelle forstand er behandlet i artiklen vektorrum .

I snævrere forstand forstås i analytisk geometri en vektor som et matematisk objekt, der beskriver en parallel forskydning i planet eller i rummet. En vektor kan repræsenteres af en pil, der forbinder et originalt billedpunkt med dets billedpunkt. Pile, der er af samme længde, parallelle og orienteret i samme retning, beskriver den samme vektor. I kartesiske koordinater er vektorer repræsenteret ved par af tal (i flyet) eller tripler (i rummet), som ofte er skrevet under hinanden (som "søjlevektorer"). Vektorer kan tilføjes og multipliceres med reelle tal ( skalarer ).

Motiveret af koordinatrepræsentation af geometriske vektorer er ofte - tupler af reelle tal, det vil sige elementer af , kaldet vektorer eller som koordinatvektorer. Dette begrundes med, at hvert -dimensionelt virkeligt vektorrum er isomorft i forhold til vektorrummet . Eksempler på sådan brug af udtrykket vektor kan findes i forretningsmatematik . ${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$

Denne artikel omhandler hovedsageligt vektorer i geometrisk forstand og om vektorer som elementer i "tuple space" . ${\ displaystyle \ mathbb {R} ^ {n}}$

Vektormængder i fysik er tæt forbundet med geometriske vektorer . Disse er fysiske størrelser, der har en størrelse og en retning og ofte repræsenteres af pile, hvis længde svarer til størrelsen af ​​mængden. Eksempler er hastighed , acceleration , momentum , kraft , elektrisk og magnetisk feltstyrke .

historie

Vektorberegning blev grundlagt af Hermann Günter Graßmann , der udgav sin Lineale Expansion Theory i 1844 , en bog med mere end tre hundrede sider. Forløberne omfatter: René Descartes og August Ferdinand Möbius , elev af Carl Friedrich Gauß . Omkring 1850 brugte den irske matematiker Matthew O'Brien vektorregning til at beskrive mekaniske fakta, men blev stort set ignoreret. Næsten på samme tid udviklede William Rowan Hamilton sin lignende teori om kvaternioner , som han udgav i 1853 i bogen Lectures on Quaternions og i 1866 i værket Elements of Quaternions . I Tyskland var vektorberegning særlig populær gennem foredrag og bøger af Alfred Bucherer , August Föppl , Carl Runge , Fischer, v. Ignatowsky og Richard Gans spredte sig.

Notation

Variabler, der står for vektorer, er ofte markeret med en pil, især i skolens matematik og fysik ( ). De er også skrevet med fed ( , eller v ), især i de engelsktalende lande . I manuskripter er dette ofte repræsenteret ved understregning ( ) eller noget lignende. Tidligere var stavningen med små Fraktur -bogstaver ( ) også almindelig, håndskrevet ved hjælp af tysk kursiv eller Sütterlin -skrift . Ofte valgte bogstaver er og . Det tilsvarende latinske bogstav uden vektormærkning står normalt for længden (mængden) af vektoren:${\ displaystyle {\ vec {a}}, {\ vec {v}}}$${\ displaystyle \ mathbf {v}}$${\ displaystyle {\ boldsymbol {v}}}$${\ displaystyle {\ understregning {v}}}$${\ displaystyle {\ mathfrak {a}}, {\ mathfrak {b}}, {\ mathfrak {v}}}$${\ displaystyle {\ vec {a}}, {\ vec {b}}, {\ vec {c}}}$${\ displaystyle {\ vec {u}}, {\ vec {v}}, {\ vec {w}}}$${\ displaystyle v = | {\ vec {v}} |}$

geometri

definition

I geometri er en vektor et objekt, der beskriver en parallel forskydning i et plan eller i rummet. Et skift kan repræsenteres af en pil, der forbinder et originalt billedpunkt med dets billedpunkt. Pile, der er parallelle, af samme længde og i samme retning beskriver den samme forskydning og repræsenterer dermed den samme vektor.For eksempel på billedet til højre, pilen fra til , pilen fra til og pilen fra for at beskrive den samme forskydning med 7 enheder til højre og 3 enheder op. De repræsenterer alle den samme vektor . Formelt kan vektorer derfor defineres som følger: ${\ displaystyle A}$${\ displaystyle A '}$${\ displaystyle B}$${\ displaystyle B '}$${\ displaystyle C}$${\ displaystyle C '}$${\ displaystyle {\ vec {v}} = {\ overrightarrow {AA '}} = {\ overrightarrow {BB'}} = {\ overrightarrow {CC '}}}$

En pil er en rettet rute, det vil sige en rute, for hvilken en rækkefølge af slutpunkterne er angivet. To pile er ækvivalente, hvis de er parallelle, af samme længde og af samme retning. Dette definerer en ækvivalensrelation på sættet med pile i flyet eller i rummet. Ækvivalensklasserne kaldes vektorer.

En anden mulighed er at identificere en vektor med den parallelle forskydning, den repræsenterer . "Vector" er så bare en anden måde at tale for "parallel shift".

Vektoren, der beskriver en forskydning, der kortlægger punktet til punktet , skrives som og grafisk repræsenteret af en pil, der peger fra punkt til punkt . Man siger: "Vektoren kortlægger op ", eller: "Vektoren forbinder og ." I dette tilfælde er punktet omtales som den aksel, udgangspunkt eller udgangspunktet og den spids eller slutpunktet af vektoren pil. Afstanden mellem de to punkter kaldes vektorens længde eller størrelse . ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle {\ overrightarrow {AB}}}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle {\ vec {a}} = {\ overretrowarrow {AB}}}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle {\ vec {a}} = {\ overretrowarrow {AB}}}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$

Den omvendte vektor, der med links, er modvektor til . Vektoren, der kortlægger et punkt på sig selv, kaldes nulvektoren og betegnes med eller . Det er den eneste vektor, der ikke kan gengives grafisk med en pil. ${\ displaystyle {\ overrightarrow {BA}}}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle {\ overrightarrow {AB}}}$${\ displaystyle {\ overrightarrow {AA}}}$${\ displaystyle A}$${\ displaystyle {\ vec {0}}}$${\ displaystyle {\ vec {o}}}$

Sted- og retningsvektorer

Vektorer kan også bruges til at angive punkter i rummet. Så punktets placering kan angives af vektoren ${\ displaystyle P}$

${\ displaystyle {\ vec {p}} = {\ overpil {OP}}}$

bliver repræsenteret. Denne vektor kaldes positionsvektoren , der tilhører punktet . Det betegner den oprindelse koordinater , som danner udgangspunktet for alle positionsvektorer. ${\ displaystyle P}$${\ displaystyle O}$

For at skelne dem fra dem omtales vektorer som beskrevet i det foregående afsnit også som retningsvektorer . To retningsvektorer er identiske, hvis de har samme størrelse og retning. Som vist kan du dog have et hvilket som helst punkt i rummet som udgangspunkt, mens positionsvektorer altid starter fra koordinaternes oprindelse.

Denne sondring er blandt andet vigtig inden for analytisk geometri. Der beskrives for eksempel en lige linje med følgende ligning:

${\ displaystyle {\ vec {x}} = {\ vec {p}} + r \ cdot {\ vec {v}}}$

Den støtte vektor er positionen vektor af en arbitrært valgt "støttepunkt" af den lige linje. Retningsvektoren angiver retlinjen for den lige linje. Fordi står for ethvert reelt tal, er positionsvektoren for ethvert punkt på den lige linje. ${\ displaystyle {\ vec {p}}}$${\ displaystyle {\ vec {v}}}$${\ displaystyle r}$${\ displaystyle {\ vec {x}}}$

Repræsentation i koordinater

Hvis der, som i figuren ovenfor, er givet et lineært koordinatsystem, kan en vektor i flyet beskrives med et ordnet par af tal, en vektor i rummet med et tal tredobbelt. Disse koordinater er som regel skrevet under hinanden som såkaldte søjlevektorer . For vektoren i planet, der beskriver skiftet med 7 enheder til højre (i retningen) og 3 enheder opad (i retningen), skriver man . Vektoren beskriver et skift med 2 enheder i -retningen og -5 enheder i -retningen, dvs. med 2 enheder til højre og 5 enheder nedad. På samme måde beskriver vektoren i rummet et skift på 3 enheder i retningen, 2 enheder i den negative retning og 4 enheder i retningen. ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle {\ vec {v}} = {\ tbinom {7} {3}}}$${\ displaystyle {\ tbinom {2} {- 5}}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle \ left ({\ begin {smallmatrix} 3 \\ - 2 \\ 4 \ end {smallmatrix}} \ right)}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$

De koordinater for en vektor kan beregnes som forskellen mellem koordinaterne for enden og udgangspunkt. I eksemplet ovenfor, og har koordinaterne og . Koordinaterne for forbindelsesvektoren beregnes derefter som følger: ${\ displaystyle A}$${\ displaystyle A '}$${\ displaystyle A (-6 | -1)}$${\ displaystyle A '(1 | 2)}$${\ displaystyle {\ vec {v}} = {\ overretrowarrow {AA '}}}$

${\ displaystyle {\ vec {v}} = {\ overrightarrow {AA '}} = {\ begin {pmatrix} 1 - ( - 6) \\ 2 - ( - 1) \ end {pmatrix}} = {\ begin {pmatrix} 7 \\ 3 \ end {pmatrix}}}$

Beløb og retning

I modsætning til skalarer har vektorer en retning. En vektor er således karakteriseret ved dens størrelse og retning. Retningen er givet på den ene side af aksepositionen og på den anden side af retningssansen . Retningsfølelsen angiver i hvilken af ​​de to retninger langs aksen vektoren peger. En ændring i tegnet i vektorens størrelse svarer til omvendelse af retningssansen.

Aritmetiske operationer

Addition og subtraktion

Den tilsætning af to geometriske vektorer svarer til udførelsen af den tilhørende skift efter hinanden. Hvis vektoren repræsenterer forskydningen, som prikken på danner kort, og til tilsvarende forskydning af punktet ved start, beskriver så forskydningen af kort: ${\ displaystyle {\ vec {a}}}$${\ displaystyle P}$${\ displaystyle Q}$${\ displaystyle {\ vec {b}}}$${\ displaystyle Q}$${\ displaystyle R}$${\ displaystyle {\ vec {a}} + {\ vec {b}}}$${\ displaystyle P}$${\ displaystyle R}$

${\ displaystyle {\ overrightarrow {PQ}} + {\ overrightarrow {QR}} = {\ overrightarrow {PR}}}$

Geometrisk kan du derfor tilføje to vektorer og ved at repræsentere de to vektorer med pile på en sådan måde, at startpunktet for den anden pil falder sammen med slutpunktet for den første pil. Summen repræsenteres derefter af pilen fra startpunktet for den første til slutpunktet for den anden pil. ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {c}} = {\ vec {a}} + {\ vec {b}}}$

Alternativt repræsenteres de to vektorer med pile med et fælles udgangspunkt, og dette tal udvides til at danne et parallelogram . Den diagonale pil fra det fælles udgangspunkt til det modsatte hjørne repræsenterer så summen af ​​de to vektorer.I fysik bruges denne konstruktion til parallelogram af kræfter .

Summen beregnes komponentmæssigt i koordinater: For summen af de to vektorer

${\ displaystyle {\ vec {a}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}}}$ og ${\ displaystyle {\ vec {b}} = {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}}}$

er gældende

${\ displaystyle {\ vec {a}} + {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} + {\ begynde {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {1} + b_ {1} \\ a_ {2} + b_ {2} \\ a_ {3} + b_ {3} \ end {pmatrix}}}$.

De associative og kommutative love gælder for tilføjelse af vektorer .

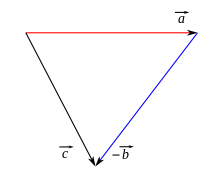
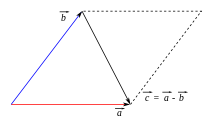
For forskellen mellem to vektorer og gælder ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

${\ displaystyle {\ vec {a}} - {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} - {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {1} -b_ {1} \\ a_ {2} -b_ {2} \\ a_ {3} -b_ {3} \ end {pmatrix}}}$.

Det kan tolkes geometrisk på to måder:

• Som summen af med den modsatte vektor af . Startpunktet for en pil, som repræsenterer den modsatte vektor af , placeres ved pilens slutpunkt, som repræsenterer.${\ displaystyle {\ vec {a}}}$${\ displaystyle - {\ vec {b}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {a}}}$
• Som vektoren, der bare tilføjer op til . Hvis og er repræsenteret med pile med det samme startpunkt, vises pilen, der fører fra slutpunktet for den anden vektor til slutpunktet for den første vektor.${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {a}} - {\ vec {b}}}$

Hvis to vektorer tilføjes (subtraheres), tilføjes deres mængder (subtraheres) kun, hvis vektorerne er kollinære og har samme orientering. I det generelle tilfælde gælder trekantens ulighed imidlertid :

${\ displaystyle \ left | {\ vec {a}} + {\ vec {b}} \ right | \ leq \ left | {\ vec {a}} \ right | + \ left | {\ vec {b}} \ højre |}$

Multiplikation med en skalar

Vektorer kan ganges med reelle tal (ofte kaldet skalarer for at skelne dem fra vektorer) ( skalarmultiplikation , også kaldet S -multiplikation):

${\ displaystyle r {\ vec {a}} = r \, {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} = {\ begin {pmatrix} ra_ {1} \\ ra_ {2} \\ ra_ {3} \ end {pmatrix}}}$

Længden af ​​den resulterende vektor er . Hvis skalaren er positiv, peger den resulterende vektor i samme retning som originalen, hvis den er negativ, i den modsatte retning. ${\ displaystyle | r | \ cdot | {\ vec {a}} |}$

Distributionsloven gælder for vektortilsætning og multiplikation med en skalar :

${\ displaystyle r \ cdot ({\ vec {a}} + {\ vec {b}}) = r {\ vec {a}} + r {\ vec {b}}}$

Det samme gælder tilføjelsen af ​​to skalarer:

${\ displaystyle (r + s) \ cdot {\ vec {a}} = r {\ vec {a}} + s {\ vec {a}}}$

Skalær produkt

Den skalarproduktet (eller indre produkt ) af to vektorer og såkaldte fordi resultatet er en skalar er noteret som eller og er ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}},}$${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}}, \ {\ vec {a}} \ circ {\ vec {b}}, \ {\ vec {a}} \ bullet {\ vec {b}}}$${\ displaystyle \ langle {{\ vec {a}}, {\ vec {b}}} \ rangle}$

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = | {\ vec {a}} | \, | {\ vec {b}} | \, \ cos \ varphi,}$

hvor er vinklen indesluttet mellem de to vektorer (se også cosinus ). Er de to vektorer vinkelret på hinanden, så som sand. ${\ displaystyle \ varphi}$${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = 0}$${\ displaystyle \ cos \ varphi = \ cos 90 ^ {\ circ} = 0}$

I det kartesiske koordinatsystem beregnes skalarproduktet

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ cdot {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = a_ {1} b_ {1} + a_ {2} b_ {2} + a_ {3 } b_ {3},}$

gælder især firkanten af ​​en vektor

${\ displaystyle {\ vec {a}} \ cdot {\ vec {a}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ cdot {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} = a_ {1} ^ {2} + a_ {2} ^ {2} + a_ {3 } ^ {2}.}$

Geometrisk kan skalarproduktet også forstås som følger (se illustration): Den ene projekterer den ene vektor vinkelret på den anden og opnår dermed vektoren . Hvis den af ​​de to vektorer omsluttede vinkel er en spids vinkel, peger den i samme retning som . I dette tilfælde opnås skalarproduktet ved at gange de to mængder af og . Det tal er positivt. Hvis det imidlertid er af en stump vinkel, så fremskrivningen af anti-parallel til og derfor prikproduktet har et negativt tegn. Hvis de to vektorer omslutter en ret vinkel ( ), er længden af ​​den projicerede vektor nul og dermed også skalarproduktet. (Hvis du bytter de to vektorer, når du gør dette, er resultatet den samme værdi.) ${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}} _ {\ vec {a}}}$${\ displaystyle \ varphi}$${\ displaystyle {\ vec {b}} _ {\ vec {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}} _ {\ vec {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle \ varphi = 90 ^ {\ circ}}$

Denne operation bruges ofte i fysik , for eksempel til at beregne arbejdet, når kraftens retning ikke falder sammen med bevægelsesretningen.

Den kommutative lov gælder for skalarproduktet

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = {\ vec {b}} \ cdot {\ vec {a}}}$

og distributionsloven

${\ displaystyle {\ vec {a}} \ cdot ({\ vec {b}} + {\ vec {c}}) = {\ vec {a}} \ cdot {\ vec {b}} + {\ vec {a}} \ cdot {\ vec {c}}.}$

Kryds produkt

Den cross produkt (også vektor produkt, ydre produkt eller vektor produkt ) (talt som ”en krydsning b”) af to vektorer i det tredimensionale euklidiske vektorrum er en vis vektor, som er vinkelret på planet udspændt af og . Længden af denne vektor er lig med arealet af parallelogrammet med siderne og så ${\ displaystyle {\ vec {a}} \ times {\ vec {b}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle | {\ vec {a}} \ times {\ vec {b}} |}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

${\ displaystyle | {\ vec {a}} \ times {\ vec {b}} | = | {\ vec {a}} | \ cdot | {\ vec {b}} | \ cdot | {\ sin \ theta } |,}$

hvor den af ​​de to vektorer omsluttede vinkel er betegnet her med . Krydsproduktet af to kollinære vektorer giver derfor nulvektoren. ${\ displaystyle \ theta}$

I det tredimensionelle kartesiske koordinatsystem kan krydsproduktet beregnes som følger:

${\ displaystyle {\ vec {a}} \ times {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ times {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {2} b_ {3} -a_ {3} b_ { 2} \\ a_ {3} b_ {1} -a_ {1} b_ {3} \\ a_ {1} b_ {2} -a_ {2} b_ {1} \ end {pmatrix}}}$

Krydsproduktet er anti-kommutativt ; det vil sige, det gælder

${\ displaystyle {\ vec {a}} \ times {\ vec {b}} = - ({\ vec {b}} \ times {\ vec {a}}).}$

Sent produkt

Kombinationen af ​​kryds og skalarprodukt i formen

${\ displaystyle ({\ vec {a}}, {\ vec {b}}, {\ vec {c}}) = ({\ vec {a}} \ times {\ vec {b}}) \ cdot { \ vec {c}}}$

kaldes et sent produkt. Resultatet er en skalar. Dens beløb er volumenet af den yngel , der er udspændt af de tre vektorer. Hvis de tre vektorer danner et retssystem , er det positivt. Hvis de danner et venstre system , er det negativt. Hvis vektorerne er lineært afhængige, så holder . ${\ displaystyle ({\ vec {a}}, {\ vec {b}}, {\ vec {c}})}$${\ displaystyle ({\ vec {a}}, {\ vec {b}}, {\ vec {c}})}$${\ displaystyle ({\ vec {a}}, {\ vec {b}}, {\ vec {c}}) = 0}$

Længde / mængde af en vektor

I kartesiske koordinater kan længden af ​​vektorer beregnes i henhold til Pythagoras sætning :

${\ displaystyle a = | {\ vec {a}} | = {\ sqrt {{a_ {1}} ^ {2} + {a_ {2}} ^ {2} + {a_ {3}} ^ {2 }}}}$

Dette svarer til den såkaldte euklidiske norm . Længden kan også angives i en alternativ notation som roden til skalarproduktet:

${\ displaystyle a = | {\ vec {a}} | = {\ sqrt {{\ vec {a}} \ cdot {\ vec {a}}}}}}$

Vektorer med længde 1 kaldes enhedsvektorer . Hvis en vektor har længden 0, er den nulvektoren.

I tilfælde af vektormængder i fysik taler man om mængden af en vektor i stedet for længden . En vektors fysiske størrelse kan ses som et par af retningen af ​​mængden som en enhedsvektor og størrelsen af ​​mængden langs denne retning. Enheden for mængden er den samme som enheden for den fysiske mængde. For eksempel hastigheden ${\ displaystyle {\ vec {v}}}$${\ displaystyle ({\ vec {e}} _ {v}, | {\ vec {v}} |)}$${\ displaystyle {\ vec {e}} _ {v}}$

${\ displaystyle {\ vec {v}} = {\ begin {pmatrix} 3 \\ - 4 \\ 0 \ end {pmatrix}} \, \ mathrm {\ frac {m} {s}}}$

af en helikopter, der flyver i konstant højde i sydøstlig retning

${\ displaystyle {\ vec {e}} _ {v} = {\ frac {1} {| {\ vec {v}} |}} {\ vec {v}} = {\ begin {pmatrix} {\ tfrac {3} {5}} \\ - {\ tfrac {4} {5}} \\ 0 \ end {pmatrix}}}$

og

${\ displaystyle | {\ vec {v}} | = {\ sqrt {3 ^ {2} + (- 4) ^ {2} + 0 ^ {2}}} \, \ mathrm {\ frac {m} { s}} = 5 \, \ mathrm {\ frac {m} {s}}}$

repræsentere. Mængden af stihastigheden for et vandret kast (starthastighed i -retning , nuværende hastighed i -retning ) kan angives som ${\ displaystyle v (t)}$${\ displaystyle x}$${\ displaystyle v_ {x}}$${\ displaystyle y}$${\ displaystyle v_ {y} (t)}$

${\ displaystyle v (t) = {| {\ vec {v (t)}} |} = {\ sqrt {v _ {\ mathrm {x}} ^ {2} + v _ {\ mathrm {y}} ^ {2}}}.}$

Dyadisk produkt

Den dyadic eller tensorial produkt eller (talt som ”en dyadic b”) af to vektorer danner en dyade. Med dyader kan en vektor kortlægges lineært på en anden vektor, se billede. Delen af ​​en vektor i vektorens retning bringes i vektorens retning og strækkes eller komprimeres. Kortlægningen udføres med ovenstående skalarprodukt: ${\ displaystyle {\ vec {a}} \ otimes {\ vec {b}}}$${\ displaystyle {\ vec {a}} {\ vec {b}}}$${\ displaystyle {\ vec {c}}}$${\ displaystyle {\ vec {b}}}$${\ displaystyle {\ vec {a}}}$

${\ displaystyle ({\ vec {a}} \ otimes {\ vec {b}}) \ cdot {\ vec {c}}: = ({\ vec {b}} \ cdot {\ vec {c}}) {\ vec {a}}}$

I det tredimensionelle kartesiske koordinatsystem kan det dyadiske produkt beregnes som følger:

${\ displaystyle {\ vec {a}} \ otimes {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ otimes {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {1} b_ {1} & a_ {1} b_ { 2} & a_ {1} b_ {3} \\ a_ {2} b_ {1} & a_ {2} b_ {2} & a_ {2} b_ {3} \\ a_ {3} b_ {1} & a_ {3} b_ {2} og a_ {3} b_ {3} \ end {pmatrix}}}$

Det dyadiske produkt er ikke kommutativt; altså generelt

${\ displaystyle {\ vec {a}} \ otimes {\ vec {b}} \ neq {\ vec {b}} \ otimes {\ vec {a}},}$

men fordelende med vektortilsætning:

${\ displaystyle {\ begin {align} ({\ vec {a}} + {\ vec {b}}) \ otimes {\ vec {c}} = {\ vec {a}} \ otimes {\ vec {c }} + {\ vec {b}} \ otimes {\ vec {c}} \\ {\ vec {a}} \ otimes ({\ vec {b}} + {\ vec {c}}) = {\ vec {a}} \ otimes {\ vec {b}} + {\ vec {a}} \ otimes {\ vec {c}} \ end {align}}}$

Det er også kompatibelt med skalarmultiplikation:

${\ displaystyle \ lambda ({\ vec {a}} \ otimes {\ vec {b}}) = (\ lambda {\ vec {a}}) \ otimes {\ vec {b}} = {\ vec {a }} \ otimes (\ lambda {\ vec {b}}) = \ lambda {\ vec {a}} \ otimes {\ vec {b}}}$

Det dyadiske produkt skaber en ny klasse af objekter af lineær algebra , matricerne og lineære kortlægninger , afhængigt af om beregninger udføres i koordinatrum eller vektorrum . Ved at forbinde flere dyader (som i ) opstår dyader på et højere niveau. Dyads er et specielt tilfælde af tensorer . Tensorer spiller en vigtig rolle i kontinuummekanik , Maxwell -ligningerne for elektromagnetisme og generel relativitet . Det formulerede tensor algebra giver et overblik over den tensor algebra . ${\ displaystyle {\ vec {a}} \ otimes {\ vec {b}} \ otimes {\ vec {c}} \ dotsm}$

Komponentnotation

Som et alternativ til notationen, der præsenteres her som kolonnevektorer, kan vektorer også repræsenteres i komponentnotation. Normalt står for de enkelte komponenter i vektoren med hensyn til standardgrundlaget . Som et resultat heraf kan de aritmetiske operationer skrives som følger med hensyn til standardgrundlaget: ${\ displaystyle a_ {i}}$${\ displaystyle {\ vec {a}}}$

	Kolonnevektorer	Komponentnotation
Addition / subtraktion	${\ displaystyle {\ vec {c}} = {\ vec {a}} \ pm {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ pm {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {1} \ pm b_ {1} \\ a_ {2} \ pm b_ {2} \\ a_ {3} \ pm b_ {3} \ end {pmatrix}}}$	${\ displaystyle c_ {i} = a_ {i} \ pm b_ {i}}$
Skalær produkt	${\ displaystyle c = {\ vec {a}} \ cdot {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ cdot {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = a_ {1} b_ {1} + a_ {2} b_ {2} + a_ {3} b_ {3}}$	${\ displaystyle c = \ sum _ {i} a_ {i} b_ {i}}$ henholdsvis: ${\ displaystyle c = a_ {i} b_ {i}}$
beløb	${\ displaystyle a = | {\ vec {a}} | = {\ sqrt {{a_ {1}} ^ {2} + {a_ {2}} ^ {2} + {a_ {3}} ^ {2 }}}}$	${\ displaystyle a = {\ sqrt {\ sum _ {i} a_ {i} ^ {2}}}}$ henholdsvis: ${\ displaystyle a = {\ sqrt {a_ {i} a_ {i}}}}$
Kryds produkt	${\ displaystyle {\ vec {c}} = {\ vec {a}} \ times {\ vec {b}} = {\ begin {pmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {pmatrix}} \ times {\ begin {pmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {2} b_ {3 } -a_ {3} b_ {2} \\ a_ {3} b_ {1} -a_ {1} b_ {3} \\ a_ {1} b_ {2} -a_ {2} b_ {1} \ end {pmatrix}}}$	${\ displaystyle c_ {i} = \ sum _ {jk} \ varepsilon _ {ijk} a_ {j} b_ {k}}$ henholdsvis: ${\ displaystyle c_ {i} = \ varepsilon _ {ijk} a_ {j} b_ {k}}$

1. ↑ ^{a b c} Brug af Einsteins summationskonvention
2. ↑ er Levi-Civita-symbolet og er +1 for lige permutationer af (1, 2, 3), -1 for ulige permutationer og 0 ellers.${\ displaystyle \ varepsilon _ {ijk}}$

Se også afsnittet Koordinater og komponenter i en vektor nedenfor.

n tupler og søjlevektorer

I generalisering af koordinatsystemet repræsentation af geometriske elementer er vektorer af så - tupler af reelle tal , kaldet vektorer, når de typiske vektorer aritmetiske operationer af addition og skalarmultiplikation der udføres med dem. Som regel skrives tuplerne som såkaldte søjlevektorer , det vil sige, at deres poster er en under den anden. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$ ${\ displaystyle n}$

Addition og skalarmultiplikation

Tilføjelsen af ​​to vektorer og skalar -multiplikationen af ​​en vektor med et tal defineres komponent for komponent: ${\ displaystyle {\ vec {x}}, {\ vec {y}} \ in \ mathbb {R} ^ {n}}$${\ displaystyle r \ in \ mathbb {R}}$

${\ displaystyle {\ vec {x}} + {\ vec {y}} = {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} + {\ begin { pmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {pmatrix}} = {\ begin {pmatrix} x_ {1} + y_ {1} \\\ vdots \\ x_ {n} + y_ {n} \ end {pmatrix}}, \ quad r {\ vec {x}} = r {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} = { \ begin {pmatrix} rx_ {1} \\\ vdots \\ rx_ {n} \ end {pmatrix}}}$

Med disse forbindelser danner sættet et vektorrum over kroppen . Dette såkaldte koordinatrum er standardeksemplet på et -dimensionalt vektorrum. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle n}$${\ displaystyle \ mathbb {R}}$

Standard skalarprodukt

Standard skalarproduktet er defineret af

${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} \ cdot {\ begynd {pmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {pmatrix}} = x_ {1} y_ {1} + \ dotsb + x_ {n} y_ {n}}$.

Med dette skalarprodukt er det et euklidisk vektorrum . ${\ displaystyle \ mathbb {R} ^ {n}}$

Multiplikation med en matrix

Hvis der er en ( ) matrix og en kolonnevektor, så kan man forstå som en enkeltkolonnematrix og danne matrix-vektorproduktet . Resultatet er en kolonnevektor i : ${\ displaystyle A \ in \ mathbb {R} ^ {m \ times n}}$${\ displaystyle m \ gange n}$${\ displaystyle {\ vec {x}} \ in \ mathbb {R} ^ {n}}$${\ displaystyle {\ vec {x}}}$${\ displaystyle \ mathbb {R} ^ {n \ gange 1}}$${\ displaystyle A \, {\ vec {x}}}$${\ displaystyle \ mathbb {R} ^ {m}}$

${\ displaystyle A \, {\ vec {x}} = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\\ vdots & \ ddots & \ vdots \\ a_ {m1} & \ prikker & a_ {mn} \ end {pmatrix}} \, {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}} = {\ begin {pmatrix} a_ {11 } x_ {1} + \ dotsb + a_ {1n} x_ {n} \\\ vdots \\ a_ {m1} x_ {1} + \ dotsb + a_ {mn} x_ {n} \ end {pmatrix}}}$

Multiplikationen med en ( ) matrix er en lineær kortlægning fra til . Hver lineær kortlægning kan repræsenteres som en multiplikation med en matrix. ${\ displaystyle m \ gange n}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$

Længde eller norm

Længden eller normen for en vektor er givet ved kvadratroden af ​​skalarproduktet med sig selv:

${\ displaystyle | {\ vec {x}} | = {\ sqrt {{\ vec {x}} \ cdot {\ vec {x}}}} = {\ sqrt {x_ {1} ^ {2} + \ dotsb + x_ {n} ^ {2}}}}$

Ud over denne euklidiske norm bruges også andre normer , se s norm .

Række- og kolonnevektorer

Hvis man betragter vektorer som matricer, så er en matrix en kolonnevektor${\ displaystyle n \ gange 1}$

${\ displaystyle {\ vec {x}} = {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}},}$

hvortil der er en matrix ${\ displaystyle 1 \ times n}$

${\ displaystyle {\ vec {x}} ^ {\ top} = (x_ {1} \ \ dotsc \ x_ {n})}$

som den tilsvarende rækkevektor , hvor den transponerede af ER. I denne notation er standardskalarproduktet ikke andet end matrixproduktet af en -Matrix med en -Matrix: ${\ displaystyle {\ vec {x}} ^ {\ top}}$${\ displaystyle {\ vec {x}}}$${\ displaystyle 1 \ times n}$${\ displaystyle n \ gange 1}$

${\ displaystyle {\ vec {x}} \ cdot {\ vec {y}} = {\ vec {x}} ^ {\ top} {\ vec {y}} = (x_ {1} \ \ dotsc \ x_ {n}) \ {\ begin {pmatrix} y_ {1} \\\ vdots \\ y_ {n} \ end {pmatrix}} = x_ {1} y_ {1} + \ dotsb + x_ {n} y_ { n}}$

Det dyadiske produkt er matrixproduktet af en matrix med en matrix og giver derefter en matrix: ${\ displaystyle n \ gange 1}$${\ displaystyle 1 \ times n}$${\ displaystyle n \ gange n}$

${\ displaystyle {\ vec {x}} \ otimes {\ vec {y}} = {\ vec {x}} \, {\ vec {y}} ^ {\ top} = {\ begin {pmatrix} x_ { 1} \\\ vdots \\ x_ {n} \ end {pmatrix}} \ (y_ {1} \ \ dotsc \ y_ {n}) = {\ begin {pmatrix} x_ {1} y_ {1} & \ ldots & x_ {1} y_ {n} \\\ vdots & \ ddots & \ vdots \\ x_ {n} y_ {1} & \ ldots & x_ {n} y_ {n} \ end {pmatrix}}}$

Egenskaber for vektorer

Lineær afhængighed

Vektorer ( ) kaldes lineært afhængige, hvis der er en løsning til følgende ligning, der ikke gælder for alle koefficienter : ${\ displaystyle {\ vec {a}} _ {1}, {\ vec {a}} _ {2}, \ dotsc, {\ vec {a}} _ {m}}$${\ displaystyle m \ geq 1}$${\ displaystyle r_ {i} = 0}$

${\ displaystyle r_ {1} \ cdot {\ vec {a}} _ {1} + r_ {2} \ cdot {\ vec {a}} _ {2} + \ dotsb + r_ {m} \ cdot {\ vec {a}} _ {m} = {\ vec {0}} {\ tekst {med}} r_ {i} \ in \ mathbb {R}}$

Men hvis der ikke kan findes koefficienter , der opfylder denne betingelse, siges det at vektorerne er lineært uafhængige .${\ displaystyle r_ {i}}$

I dette tilfælde gælder følgende: Nulvektoren er lineært afhængig, hver anden vektor er lineært uafhængig. ${\ displaystyle m = 1}$

I tilfælde af lineær afhængighed kan mindst en af ​​vektorerne repræsenteres som en lineær kombination af de andre. ${\ displaystyle m> 1}$

For at definere et koordinatsystem for et -dimensionalt rum har man brug for præcis lineært uafhængige basisvektorer . Derefter kan hver vektor i dette rum skrives på en unik måde som en lineær kombination af basisvektorerne. Mere end vektorer i -dimensionalt rum er altid lineært afhængige. ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$

Kollinearitet af to vektorer

To lineært afhængige vektorer og kaldes også kollinære . I det tredimensionelle rum gælder dem ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

${\ displaystyle {\ vec {a}} \ times {\ vec {b}} = {\ vec {0}}.}$

Hver vektor er kollinær med nulvektoren. Men hvis der er to vektorer, der er forskellige fra nulvektoren, så er de kollinære, hvis og kun hvis

${\ displaystyle {\ vec {a}} = r \ cdot {\ vec {b}}}$

for man er opfyldt. De er parallelle når de er positive og anti-parallelle når de er negative. ${\ displaystyle r \ in \ mathbb {R} \ setminus \ {0 \}}$${\ displaystyle r}$${\ displaystyle r}$

Ortogonalitet

To vektorer og er ortogonale, hvis deres skalære produkt er 0: ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}} = 0}$

For geometriske vektorer med positiv længde betyder det, at de omslutter en ret vinkel , se skalarprodukt . Nulvektoren er ortogonal i forhold til hver vektor.

Normalisering

En vektor (læs "et tag") kaldes en enhedsvektor eller normaliseres, hvis den har længden 1. En vektor normaliseres ved at dividere den med dens længde, dvs. dvs. ganget med det gensidige af dens længde:${\ displaystyle {\ hat {a}}}$${\ displaystyle {\ vec {a}} \ neq {\ vec {0}}}$

${\ displaystyle {\ hat {a}} = {\ frac {\ vec {a}} {| {\ vec {a}} |}}}$

Vektoren har samme retning som , men længde 1. Andre notationer for er , eller .${\ displaystyle {\ hat {a}}}$${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ hat {a}}}$${\ displaystyle {\ vec {e}} _ {a}}$${\ displaystyle {\ vec {a}} _ {0}}$${\ displaystyle {\ vec {a}} {} ^ {\ circ}}$

Enhedsvektorer er vigtige, når de repræsenterer koordinatsystemer .

Koordinater og komponenter i en vektor

Det mest almindelige koordinatsystem, det kartesiske , er f.eks. Som et ortonormale ordning , fordi det af de tre indbyrdes ortogonale enhedsvektorer , og den standard basen er fastklemt. De koordinater en vektor derefter de skalære produkter af vektoren med basisvektorer: ${\ displaystyle {\ hat {e}} _ {1}}$${\ displaystyle {\ hat {e}} _ {2}}$${\ displaystyle {\ hat {e}} _ {3}}$

${\ displaystyle a_ {i} = {\ vec {a}} \ cdot {\ hat {e}} _ {i}}$

Så hver vektor kan repræsenteres som en lineær kombination af basisvektorerne ved at skrive den som summen af ​​dens komponenter i forhold til grundlaget:

${\ displaystyle {\ vec {a}} = \ sum _ {i = 1} ^ {3} \ venstre ({\ vec {a}} \ cdot {\ hat {e}} _ {i} \ højre) { \ hat {e}} _ {i} = \ venstre ({\ vec {a}} \ cdot {\ hat {e}} _ {1} \ højre) {\ hat {e}} _ {1} + \ venstre ({\ vec {a}} \ cdot {\ hat {e}} _ {2} \ højre) {\ hat {e}} _ {2} + \ venstre ({\ vec {a}} \ cdot { \ hat {e}} _ {3} \ right) {\ hat {e}} _ {3}}$

Ved at skifte til et andet ortonormalt grundlag får vektoren forskellige koordinater og forskellige komponenter: ${\ displaystyle {\ hat {g}} _ {1,2,3}}$${\ displaystyle a_ {i} ^ {\ prime} = {\ vec {a}} \ cdot {\ hat {g}} _ {i}}$

${\ displaystyle {\ vec {a}} = \ sum _ {i = 1} ^ {3} \ venstre ({\ vec {a}} \ cdot {\ hat {g}} _ {i} \ højre) { \ hat {g}} _ {i} = \ venstre ({\ vec {a}} \ cdot {\ hat {g}} _ {1} \ højre) {\ hat {g}} _ {1} + \ venstre ({\ vec {a}} \ cdot {\ hat {g}} _ {2} \ højre) {\ hat {g}} _ {2} + \ venstre ({\ vec {a}} \ cdot { \ hat {g}} _ {3} \ right) {\ hat {g}} _ {3}}$

Mere generelt kan tre vilkårlige, men lineært uafhængige vektorer bruges som vektorrumsgrundlag.

Generaliseringer

Definitionen af ​​vektoren i lineær algebra som et element i et vektorrum er en meget mere omfattende, som ud over de konventionelle geometriske vektorer omfatter en lang række matematiske objekter ( tal , sekvenser , funktioner og transformationer ).

På den anden side er vektorer kun et-trins tensorer ; H. Tensorer med kun et indeks.

Vektorer i fysik

Vektormængder i det euklidiske rum i vores opfattelse

I klassisk fysik forstås fysiske størrelser, der har en størrelse og en retning , som vektorer i det euklidiske rum . Eksempler på dette er placeringen, hastigheden , accelerationen , kraften osv. De kan sammenlignes med skalære fysiske størrelser, der kun har en størrelse, men ingen retning, som f.eks. B. Volumen , masse , ladning , temperatur osv.

Denne opfattelse af rettede fysiske størrelser som vektorer er en anvendelse af geometriske vektorer. Retningen af ​​den fysiske mængde tager stedet for skiftretningen. Deres mængde svarer til forskydningen af ​​en geometrisk vektor. Repræsentationen af ​​sådanne mængder med pile af en vis længde illustrerer både deres retning og størrelse. Følgelig gælder alt, hvad der allerede er blevet sagt om geometriske vektorer, også for vektormængder i fysik, især hvad der er blevet sagt om aritmetiske operationer og grafisk illustration.

Fysiske mængder kan kun tilføjes, hvis de er mængder af samme mængdetype . Dette gælder også, hvis man betragter dem som vektorer. Tilføjelsen er z. B. illustreret ved parallelogrammet af kræfter . Vektorsummer er af enestående betydning i statik , f.eks. B. i definitionen af ​​kræfternes ligevægt . ${\ displaystyle \ sum {\ vec {F}} _ {i} = 0}$

Den dot produkt anvendes, når projektionen af en vektor i retning af en anden er vigtig. For eksempel forstås det fysiske udtryk arbejde som et produkt af en kraft og en vej i kraftens retning. Derfor beregnes arbejdet ved hjælp af skalarproduktet af kraften og stien. Derudover er skalarproduktet vigtigt i komponentnedbrydningen af ​​en vektor. Den tværs af produkter, på den anden side, anvendes overalt, hvor en lov følger den tre-finger regel , f.eks B. Lorentz kraft eller drejningsmoment . For både skalarproduktet og krydsproduktet opnås enheden af ​​den resulterende fysiske mængde ved at multiplicere enhederne for begge faktorer.

Hvis en fysisk vektor i sig selv er en funktion af placeringen, taler man om et vektorfelt . Det kan illustreres ved feltlinjer , tangenten til feltlinjen angiver vektorens retning . Den mængde af vektoren er repræsenteret af tætheden af feltlinierne. Eksempler er de elektriske og magnetiske felter samt hastighedsfelterne i strømme . I den matematiske behandling af felterne viser vektoranalyse sig at være et ekstremt vigtigt redskab, f.eks. B. i elektrodynamik eller i væskemekanik .

Vektorer i ikke-euklidiske rum i relativistisk fysik

I relativitetsteorien, den ikke - euklidiske fire - dimensionelle rum - tid tager i stedet for tre-dimensionelle euklidisk rum . Vektormængder, såsom hastigheden på fire eller impulsen på fire, er derfor her repræsenteret som fire-dimensionelle vektorer .

Transformationsadfærd af vektorer

I fysik er vektorer (også) karakteriseret ved deres transformationsadfærd ved ændring af referencesystemer .

Polære og aksiale vektorer

Afhængig af transformationsadfærden under punktrefleksioner af placeringen skelnes der mellem polære og aksiale vektorer , også kaldet tryk- og rotationsvektorer i ældre litteratur: I euklidiske vektorrum ændres hver vektor til sit negative i rumlig punktrefleksion, mens aksial vektorer forbliver uændrede. For eksempel ændrer placeringen, hastigheden, momentum og det elektriske felt deres tegn i tilfælde af rumlig punktrefleksion , men ikke vinkelmomentet eller magnetfeltet. Polare og aksiale vektorer er elementer i forskellige vektorrum på grund af deres forskellige transformationsadfærd. Krydsproduktet skal ses som en bilinear kortlægning af to vektorrum til et tredje.

Denne opfattelse i fysik afhænger af, om du arbejder i euklidisk eller ikke-euklidisk rum.

Transformationsadfærd i det euklidiske og Minkowski -rum

For det fysiske vektorbegreb er transformationsadfærden under den isometriske gruppe af den tilsvarende metrik i det underliggende rum vigtig. Klassisk mekanikkes tredimensionelle rum er modelleret som euklidisk fladt rum, mens relativitetsteoriens fire-dimensionelle rumtid er forsynet som Minkowski-rum med en buet metrisk. Disse rum er mangfoldige , hvor vektorer repræsenterer kontravariant tensorer af den første orden, hvilket bestemmer deres transformationsadfærd. De isometriske grupper er rotationsgruppen i det euklidiske rum og Lorentz -gruppen i Minkowski -rummet .

Ikke alle vektorer i tredimensionel er dele af firvektorer. For eksempel transformeres vinkelmomentet ikke under Lorentz-transformationer som en del af en fire-vektor, men sammen med det oprindelige energicenter som de seks komponenter i en antisymmetrisk tensor . På samme måde transformeres den elektriske og magnetiske feltstyrke som de seks komponenter i en antisymmetrisk tensor.

Mangepartikelsystemer med partikler er beskrevet med vektorer i -dimensionelle vektorrum, hvor den tredimensionelle roterende gruppe virker separat. ${\ displaystyle n}$${\ displaystyle 3n}$

Yderligere anvendelser af udtrykket vektor i fysik

Multi- partikel systemer af partikler er beskrevet af vektorer i dimensionale vektorrum, eller - i Hamiltonian mekanik  - i dimensionale faserum , som ikke alene de rumlige koordinater, men også pulsen koordinater. Endelig er tilstande for kvantemekaniske systemer repræsenteret som vektorer i funktionsrum. Bra-Ket- notationen, som blev introduceret af Paul Dirac , er især nyttig her. ${\ displaystyle n}$${\ displaystyle 3n}$${\ displaystyle 6n}$

litteratur

• Kurt Bohner, Peter Ihlenburg, Roland Ott: Matematik for erhvervsgymnasier - lineær algebra - vektorgeometri . Merkur, Rinteln 2004. ISBN 3-8120-0552-2 .
• Klaus Jänich : Lineær algebra. 10. udgave. Springer, Berlin 2004. ISBN 3-540-40207-1 .
• Lothar Papula : Matematik for ingeniører og naturforskere. Bind 1. 11. udgave, Vieweg, Wiesbaden 2007, ISBN 978-3-8348-0224-8 .

Weblinks

• Ronny Harbich: vektorberegning til gymnasial eksamen. På: fabulierer.de.
• Vektorer. På: mathe-online.at.
• Historien om vektorer. På: matematik.mcgill.ca.

Individuelle beviser

1. ^ Walter Gellert, Herbert Küstner, Manfred Hellwich, Herbert Kästner (red.): Lille encyklopædi af matematik. Leipzig 1970, s. 545.
2. ↑ [1]
3. ↑ Hermann Günter Grassmann: Den lineære ekspansion teori en ny gren af matematikken: Repræsenterede og forklares gennem ansøgninger til de andre grene af matematik, samt til statik, mekanikere, teorien om magnetisme og crystallonomy . O. Wigand, 1844. 
4. ^ Josiah Willard Gibbs: Kvaternioner og udvidelsesteorien . I: Naturen . tape 44 , nej. 1126 , 1891, s. 79-82 , doi : 10.1038 / 044079b0 . 
5. ^ WR Hamilton: Foredrag om Quaternions . Hodges og Smith, Dublin 1853. 
6. ↑ WRS Hamilton: Elements of Quaternions: Bind: 1 . Longmans, Green & Company, 1866 ( Google Books ). 
7. ^ WRS Hamilton, CJ Joly: Elementer af kvaternioner. Bind: 2 . Longmans, Green & Company, 1901. 
8. ^ AEH Love, H. Polster: Teoretisk mekanik. En indledende afhandling om mekanikkens principper . Springer, 2013, ISBN 978-3-642-52592-6 ( begrænset forhåndsvisning i Google bogsøgning ). 
9. ↑ Jessica Scholz: Teknisk mekanik 1: Statik. Kraftegenskaber. ingenieurkurse.de, adgang til 31. juli 2017 . 
10. ↑ Introduktion til vektorregning. Wiley Information Services - Chamgaroo, adgang 31. juli 2017 . 
11. ↑ Raymond A. Serway, John W. Jewett: Principper for fysik: En Calculus-baserede tekst. Bind 1, Udgiver: Cengage Learning, 2006, ISBN 9780534491437 , s. 19, begrænset forhåndsvisning i Google Bogsøgning
12. ^ Lambach schweizisk matematik for gymnasier, kursusniveau, Baden-Württemberg. Ernst Klett Verlag, Stuttgart 2009, ISBN 978-3-12-735301-3 , side 243.
13. ^ Fritz Reinhardt, Heinrich Soeder: dtv -atlas for matematik. Bind I: Grundlæggende, algebra og geometri. 3. udgave, Deutscher Taschenbuch Verlag, München 1978, s.191.
14. ↑ GRIMSEHL: Textbook of Physics, bind I.. Leipzig 1954, side 577-578..