Nul

Grafiske nuller: enkelt nul med ændring af tegn (dvs. med nulkryds ), dobbelt nul uden ændring af tegn

Nul er et begreb, der bruges i matematik relateret til funktioner .

definition

I en funktion er nuller de værdier i det oprindelige sæt (af definitionsområdet ), for hvilke elementet i målsæt (i værdiområdet ), der er tildelt i forbindelse med kortlægningen, er nul ( ). ${\ displaystyle D}$${\ displaystyle W}$${\ displaystyle 0 \ i W}$

I matematisk praksis er disse ofte funktioner af typen

${\ displaystyle f \ colon D \ to \ mathbb {R}}$ med ${\ displaystyle D \ subseteq \ mathbb {R}}$

eller

${\ displaystyle f \ colon D \ to \ mathbb {C}}$ med ${\ displaystyle D \ subseteq \ mathbb {R}.}$

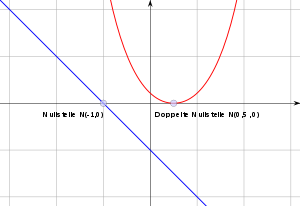
Når en funktion vises som en graf i et kartesisk koordinatsystem ( ), er disse punkter på grafen på aksen, dvs. skæringspunkt eller kontaktpunkter for funktioner, der er kontinuerlige på dette punkt . ${\ displaystyle D \ til \ mathbb {R}}$${\ displaystyle y = f (x)}$${\ displaystyle x}$

Nuller af polynomfunktioner er også kendt som rødder .

Nulstilling af reelt værdsatte funktioner

definition

Et element i den definition sæt af en funktion kaldes nul på hvis besidder. Man siger da også: har et nul på , eller forsvinder på det tidspunkt${\ displaystyle x_ {0}}$ ${\ displaystyle D}$ ${\ displaystyle f \ colon D \ to \ mathbb {R}}$${\ displaystyle f}$${\ displaystyle f \ venstre (x_ {0} \ højre) = 0}$${\ displaystyle f}$${\ displaystyle x_ {0}}$${\ displaystyle f}$ ${\ displaystyle x_ {0}.}$

eksempel

${\ displaystyle f \ venstre (x \ højre) = x ^ {2} -9}$

3 og −3 er nuller af funktionen , fordi og . ${\ displaystyle f}$${\ displaystyle f (3) = 3 ^ {2} -9 = 0}$${\ displaystyle f (-3) = (-3) ^ {2} -9 = 0}$

0 er ikke et nul, fordi . ${\ displaystyle f (0) = 0 ^ {2} -9 = -9 \ neq 0}$

Flere nuller

Definitioner

Polynom med nuller af orden 1, 2 og 3

Hvis den er kontinuerlig (f.eks. En polynomfunktion) og differentierbar ved nul , kan nulet "splittes ud". Mere præcist: der er en kontinuerlig funktion , så det for alle . ${\ displaystyle f \ colon D \ to \ mathbb {R}}$${\ displaystyle x_ {0} \ i D}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle g \ colon D \ to \ mathbb {R}}$${\ displaystyle f (x) = (x-x_ {0}) \, g (x)}$${\ displaystyle x \ i D}$

Der er derefter to sager:

1. ${\ displaystyle g (x_ {0}) \ neq 0}$. I dette tilfælde kaldes det et simpelt nul.${\ displaystyle x_ {0}}$
2. ${\ displaystyle g (x_ {0}) = 0}$, dvs. har også i et nul. Med andre ord, selv efter roden af det er blevet opdelt, er stadig et nul. I dette tilfælde kalder man et multiplum nul på .${\ displaystyle g}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle f}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle f}$

For at afgøre, om det er et enkelt eller et multiple nul, bruger man det faktum, at værdien er lig med derivatet af på det tidspunkt . For en differentierbar funktion får man følgende kriterium: ${\ displaystyle x_ {0}}$${\ displaystyle g (x_ {0})}$${\ displaystyle f}$${\ displaystyle x_ {0}}$${\ displaystyle f}$

Et nul på er et multipelt nul, hvis og kun hvis det er.${\ displaystyle x_ {0}}$${\ displaystyle f}$${\ displaystyle f '(x_ {0}) = 0}$

Hvis det oftere er differentierbart, kan denne proces gentages. Den ene definerer: ${\ displaystyle f}$

Lad det være et naturligt tal . En (mindst) gange differentierbar funktion på et åbent delsæt har en (minimum) - flere nul eller en nul rækkefølge (mindst) når sig selv og de første derivater af på stedet antager værdien nul: ${\ displaystyle k}$${\ displaystyle (k-1)}$${\ displaystyle f \ colon D \ to \ mathbb {R}}$${\ displaystyle D \ subseteq \ mathbb {R}}$${\ displaystyle x_ {0} \ i D}$${\ displaystyle k}$ ${\ displaystyle k}$${\ displaystyle f}$${\ displaystyle k-1}$ ${\ displaystyle f}$${\ displaystyle x_ {0}}$

${\ displaystyle f (x_ {0}) = 0, \ quad f '(x_ {0}) = 0, \ quad f' '(x_ {0}) = 0, \ quad \ dotsc, \ quad f ^ { (k-1)} (x_ {0}) = 0.}$

Vær nu mindst anderledes. Er et -fold nul, men ikke et -fold, så ${\ displaystyle f}$${\ displaystyle k}$${\ displaystyle x_ {0}}$${\ displaystyle k}$${\ displaystyle (k + 1)}$

${\ displaystyle f (x_ {0}) = 0, \ quad f '(x_ {0}) = 0, \ quad f' '(x_ {0}) = 0, \ quad \ dotsc, \ quad f ^ { (k-1)} (x_ {0}) = 0, \ quad f ^ {(k)} (x_ {0}) \ neq 0,}$

det er hvad nulens rækkefølge eller mangfoldighed kaldes. ${\ displaystyle k}$

eksempel

${\ displaystyle f (x) = x ^ {3} -3x ^ {2} + 3x -1}$

med derivaterne

${\ displaystyle f '(x) = 3x ^ {2} -6x + 3, \ quad f' '(x) = 6x -6, \ quad f' '' (x) = 6}$.

Det er rigtigt, at der er et nul på . Gælder yderligere ${\ displaystyle f (1) = 1-3 + 3-1 = 0}$${\ displaystyle x_ {0} = 1}$${\ displaystyle f}$

${\ displaystyle f '(1) = 3-6 + 3 = 0, \ quad f' '(1) = 6-6 = 0, \ quad}$ men ${\ displaystyle f '' '(1) = 6 \ neq 0.}$

Således er 1 et tredobbelt, men ikke et firdoblet nul på , dvs. et nul af multipliciteten 3. ${\ displaystyle f}$

Andre ejendomme

• En funktion har et -fold nul på hvis og kun hvis har et nul og et -foldet nul ved .${\ displaystyle f}$${\ displaystyle k}$${\ displaystyle x_ {0}}$${\ displaystyle f}$${\ displaystyle f '}$${\ displaystyle (k-1)}$${\ displaystyle x_ {0}}$
• En -tid kontinuerlig differentierbar funktion har et mindst -fold nul på hvis og kun hvis der er en kontinuerlig funktion sådan${\ displaystyle (k-1)}$${\ displaystyle f}$${\ displaystyle k}$${\ displaystyle x_ {0}}$ ${\ displaystyle g}$

${\ displaystyle f (x) = (x-x_ {0}) ^ {k-1} g (x)}$ og ${\ displaystyle g (x_ {0}) = 0}$

er gældende.

• En -tid kontinuerlig differentierbar funktion har et nul af multipliciteten, hvis og kun hvis der er en kontinuerlig funktion sådan${\ displaystyle k}$${\ displaystyle f}$${\ displaystyle x_ {0}}$${\ displaystyle k}$ ${\ displaystyle g}$

${\ displaystyle f (x) = (x-x_ {0}) ^ {k} g (x)}$ og ${\ displaystyle g (x_ {0}) \ neq 0}$

er gældende.

• Funktionen

${\ displaystyle f (x) = {\ begin {cases} \ exp \ left (- {\ frac {1} {x ^ {2}}} \ right) & {\ mbox {if}} \ x \ neq 0 \\ 0 & {\ mbox {if}} \ x = 0, \ end {cases}}}$

har et nul af rækkefølgen uendeligt ved 0 og er derfor ikke analytisk .

Eksistens og beregning af nuller

Eksistensen af ​​et nul kan ofte udledes indirekte af den mellemliggende værdisætning: Hvis af to funktionsværdier , en kontinuerlig funktion, er en positiv og en er negativ, så er der mindst et nul mellem og . (For at sige det klart, funktionsgrafen, der forbinder de to punkter og skal krydse -aksen.) ${\ displaystyle f (a)}$${\ displaystyle f (b)}$${\ displaystyle f}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle (a, f (a))}$${\ displaystyle (b, f (b))}$${\ displaystyle x}$

Afhængigt af funktionen kan det være svært eller umuligt at bestemme nuller eksplicit, dvs. H. ligningen

${\ displaystyle f (x) = 0}$

efter opløsning. I dette tilfælde kan omtrentlige værdier for nuller beregnes ved hjælp af forskellige numeriske metoder , f.eks. Halvering (intervalhalvningsmetode), Regula falsi eller en passende fastpunkts iteration for kontinuerlige funktioner, Newton- eller Halley -metoden til differentierbare funktioner, Weierstraß (Durand -Kerner) -Verfahrens eller Bairstow metode til polynomer bestemt. ${\ displaystyle x}$

På listen over numeriske metoder kan du finde nulpunktsøgningen under kapitlet Ikke -lineære ligningssystemer .

Nulstilling af polynomiske funktioner

Hvis en ring og et polynom er forbi , kaldes et element nul for , hvis substitutionen i nul resulterer i: ${\ displaystyle R}$${\ displaystyle p \ i R [X]}$${\ displaystyle R}$${\ displaystyle x \ i R}$${\ displaystyle p}$${\ displaystyle x}$${\ displaystyle p}$

${\ displaystyle p (x) = 0.}$

Hvis en ringhomomorfisme, kan nuller af in defineres analogt . ${\ displaystyle R \ til S}$${\ displaystyle p}$${\ displaystyle S}$

Ved hjælp af den polynomiske opdeling kan man vise, at der er et nul på hvis og kun hvis er delelig med , dvs. dvs. hvis der er et polynom sådan ${\ displaystyle x \ i R}$${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle Xx}$${\ displaystyle q}$

${\ displaystyle p (X) = (Xx) q (X)}$

er gældende. Denne erklæring kaldes undertiden nulsættet ; Der er imidlertid risiko for forveksling med Hilberts nul -sæt .

A - flere nul eller nul af ordren er et element , så det kan deles med . Man kalder også den mangfoldighed eller mangfoldighed af nul. ${\ displaystyle k}$ ${\ displaystyle k}$${\ displaystyle x \ i R}$${\ displaystyle p}$${\ displaystyle (Xx) ^ {k}}$${\ displaystyle k}$

Bestemmelse af nuller af polynomer i lille grad

For polynomer over et legeme, hvis grad er højst fire, er der generelle løsningsformler med radikaler til direkte at bestemme nuller:

• Grad 1: Se lineær ligning . Polynomet har nul .${\ displaystyle ax + b}$${\ displaystyle x = {\ tfrac {-b} {a}}}$
• Grad 2: Se kvadratisk ligning .
• Grad 3: Se kubisk ligning .
• Grad 4: Se kvartsligning .

Polynomier med heltalskoefficienter

Hvis et polynom med heltalskoefficienter, er hvert heltal nul en faktor på . ${\ displaystyle a_ {n} X ^ {n} + a_ {n-1} X ^ {n-1} + \ dotsb + a_ {1} X + a_ {0}}$${\ displaystyle a_ {0}}$

Fra Gauss lemma følger det: Hvis et normaliseret polynom med heltalskoefficienter, så er hvert rationelt nul et heltal og dermed en divisor af . ${\ displaystyle X ^ {n} + a_ {n-1} X ^ {n-1} + \ dotsb + a_ {1} X + a_ {0}}$${\ displaystyle a_ {0}}$

Eksempel:

Delerne af det absolutte udtryk for er ikke nuller, så de har ikke noget rationelt nul. Da hver faktorisering af skulle indeholde en lineær faktor, følger det, at over er ureducerbart . ${\ displaystyle -2, -1,1,2}$${\ displaystyle p (X) = X ^ {3} -X -2}$${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle \ mathbb {Q}}$

Polynomier med reelle koefficienter

Polynomer af ulige grader over de reelle tal har altid mindst et reelt nul; dette følger af den midlertidige værdisætning . En anden grund (forudsat at grundsætningen om algebra allerede er tilgængelig) er følgende: Virkelig komplekse nuller af rigtige polynomer fremstår altid som par komplekse konjugerede tal. Polynomier med lige eller ulige grader har altid et lige eller et ulige antal reelle nuller, hvis man tæller hvert nul i henhold til dets mangfoldighed. En anvendelse af sidstnævnte princip er den numeriske Bairstow -metode .

Eksempel:

Polynomet har nul , som let kan gættes som en deler af det absolutte udtryk. Dette giver ved polynomisk opdeling${\ displaystyle X ^ {3} -2X + 4}$${\ displaystyle -2}$

${\ displaystyle X ^ {3} -2X + 4 = (X + 2) (X ^ {2} -2X + 2),}$

hvorfra de to komplekse konjugerede nuller og resultat. ${\ displaystyle 1+ \ mathrm {i}}$${\ displaystyle 1- \ mathrm {i}}$

Polynomier med kun rigtige nuller

Hvis et polynom, hvis nuller alle er virkelige, ligger disse i intervallet med slutpunkterne ${\ displaystyle P (X) = X ^ {n} + a_ {n-1} X ^ {n-1} + \ dotsb + a_ {1} X + a_ {0}}$

${\ displaystyle x_ {1,2} =-{\ frac {a_ {n-1}} {n}} \ pm {\ frac {n-1} {n}} {\ sqrt {a_ {n-1} ^ {2}-{\ frac {2n} {n-1}} a_ {n-2}}}}$

Eksempel:

Polynomet har de fire virkelige rødder −3, −2, −1 og 1. Brug af intervallformelresultaterne ${\ displaystyle P (X) = X ^ {4} + 5X ^ {3} + 5X ^ {2} -5X -6}$

${\ displaystyle x_ {1,2} = - {\ frac {5} {4}} \ pm {\ frac {3} {4}} {\ sqrt {\ frac {35} {3}}}}$.

Intervallet er afrundet

I = [-3.812; 1.312].

Nuller er derfor i det fundne interval.

For formlen ændres til den velkendte pq-formel . ${\ displaystyle n = 2}$

Polynomier med komplekse koefficienter

Den grundlæggende sætning i algebra siger: Hvert ikke-konstant polynom over de komplekse tal har mindst et nul. Ved gentagne gange at opdele lineære faktorer i nuller opnår man udsagnet om, at hvert polynom

${\ displaystyle p (X) = a_ {n} X ^ {n} + a_ {n-1} X ^ {n-1} + \ dotsb + a_ {1} X + a_ {0} \ quad (a_ { n} \ neq 0)}$

om de komplekse tal i formen

${\ displaystyle p (X) = a_ {n} (X-x_ {1}) ^ {m_ {1}} \ dotsm (X-x_ {k}) ^ {m_ {k}}}$

lad os skrive. Her er de forskellige nuller af og deres respektive multipler. ${\ displaystyle x_ {1}, \ dotsc, x_ {k}}$${\ displaystyle p}$${\ displaystyle m_ {1}, \ dotsc, m_ {k}}$

Polynomer over fuldt evaluerede organer

Lad det være et fuldt evalueret felt med evalueringsring og restklassefelt , og lad det være et normaliseret polynom. Af Hensels lemma følger det: Hvis reduktionen har et simpelt nul i , så har det et nul i . ${\ displaystyle K}$${\ displaystyle A}$${\ displaystyle k}$${\ displaystyle p \ i A [X]}$${\ displaystyle {\ bar {p}} \ i k [X]}$${\ displaystyle k}$${\ displaystyle p}$${\ displaystyle A}$

Eksempel:

Lad det være feltet med p -adiske tal for et primtal . Så er og . Polynomet nedbrydes i forskellige lineære faktorer, så det har også præcis nuller, dvs. dvs. indeholder -th rødder af enhed . ${\ displaystyle K = \ mathbb {Q} _ {p}}$${\ displaystyle p}$${\ displaystyle A = \ mathbb {Z} _ {p}}$${\ displaystyle k = \ mathbb {F} _ {p}}$${\ displaystyle X ^ {p -1} -1 \ in \ mathbb {Z} _ {p} [X]}$${\ displaystyle \ mathbb {F} _ {p}}$${\ displaystyle \ mathbb {Z} _ {p}}$${\ displaystyle p-1}$${\ displaystyle \ mathbb {Z} _ {p}}$${\ displaystyle (p-1)}$

Weblinks

Wiktionary: Nulpunkt  - forklaringer på betydninger, ordoprindelse, synonymer, oversættelser