Magisk firkant

16 5 9 4. 2 11 7. 14. 3 10 6. 15. 13 8. 12. 1

Yang Hui -pladsen

En magisk firkant er et firkantet arrangement af tal eller bogstaver, der opfylder visse krav.

definition

Definitionen på en normal magisk firkant er:

Kantlængden bruges som rækkefølgen af de magiske firkanter. ${\ displaystyle n}$

Det kan også ses, at enhver aritmetisk sekvens er egnet til en magisk firkant. Der er stadig mange varianter af magiske firkanter, for hvilke ikke alle disse betingelser er opfyldt, eller der kræves yderligere begrænsninger (se nedenfor ).

Semimagisk firkant

Antal firkanter, hvor de to diagonaler ikke også resulterer i det magiske tal eller målsummen, betragtes som mislykkede og dissonante . De bestræber sig på at løse modsætningen. Disse fejlede firkanter er kendt som semi -magiske firkanter.

3. orden semimagisk firkant med 7’eren i det midterste felt og tallene 1 til 9.

9	2	4.
5	7.	3
1	6.	8.

Der er to måder at løse modsætningen i firkantede firkanter. Den første måde er at justere det midterste element, samtidig med at målmængden bevares. Den anden måde ændrer måltotalen med det midterste element uændret. Man kan altid finde rigtige løsninger med enighed af tre elementer. Løsninger med mere end tre matchende elementer er derfor af interesse.

Beregning af det magiske tal

Total af serien kaldes det magiske tal . Det er let at se, at det magiske tal skal være gange summen af ​​tallene fra 1 til : ${\ displaystyle 1 / n}$${\ displaystyle n ^ {2}}$

${\ displaystyle S_ {n} = {\ frac {1} {n}} \ cdot \ sum _ {x = 1} ^ {n ^ {2}} x = {\ frac {1} {n}} \ cdot {\ frac {n ^ {2} (n ^ {2} +1)} {2}} = {\ frac {n (n ^ {2} +1)} {2}} = {\ frac {n ^ {3} + n} {2}}}$

Fordi: være summen af ​​tallene i en linje. Vi har linjer, der alle skal have samme liniesumtal; og summen over alle rækker, dvs. er lig med summen af ​​alle poster i kvadratet, dvs. identisk med ( Gaussisk sumformel ). ${\ displaystyle ZS}$${\ displaystyle n}$${\ displaystyle n \ cdot ZS}$${\ displaystyle \ textstyle \ sum _ {k = 1} ^ {n ^ {2}} k = {\ frac {n ^ {2} \ cdot (n ^ {2} +1)} {2}}}$

De første magiske tal, der starter med, er ${\ displaystyle n = 0}$

0, 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, ... (sekvens A006003 i OEIS ).

De tre første udtryk i dette er hypotetiske. En magisk firkant med kantlængde 1 er triviel. For kantlængde 2 er der ingen løsning med fire forskellige tal.

Ækvivalens og standardform

Det er indlysende, at rotation med 90 °, 180 ° og 270 ° samt refleksion over hovedakser og diagonaler gør en magisk firkant til en magisk firkant. Disse otte magiske firkanter er ækvivalente; det er nok at undersøge en af ​​dem. Det er blevet almindelig praksis at bruge standard Frénicle -formularen her :

• Elementet i øverste venstre hjørne [1,1] er det mindste af de fire elementer i hjørnerne.
• Elementet til højre for det [1,2] er mindre end elementet nedenfor [2,1].

Komplement til den normale magiske firkant

Enhver normal magisk firkant kan suppleres. For at danne den komplementære firkant, gang alle poster med −1 og tilføj derefter konstanten til hver post . Elementerne på startpladsen og i komplementet supplerer hinanden . Den komplementære firkant har samme struktur som startpladsen. Komplementets dannelse er ikke en udvekslingsoperation, da det ikke er uafhængigt af startpladens struktur. Magiske firkanter med visse strukturer kan være selvkomplementerende, dvs. Det vil sige, at komplementet derefter svarer til startpladsen. Af de 12 strukturer i orden 4 er de magiske firkanter i 3. og 6. struktur selvkomplementerende. ${\ displaystyle n ^ {2} +1}$${\ displaystyle n ^ {2} +1}$

Sammenligning af magiske firkanter

Den nøjagtige sammenligning foretages ved at placere de magiske firkanter i løsningssættet i det homogene lineære ligningssystem. Dette svarer til klassificeringen i det ikke-geometriske vektorrum. Hver magisk firkant har sit præcist definerbare sted i løsningssættet. Løsningen er et glimrende eksempel på et ikke-geometrisk vektorrum. I tilfælde af magiske firkanter af en højere orden når klassificeringsmetoden fantasiens grænser. Det er dog didaktisk meget interessant for 3. og 4. ordens magiske firkanter. I tilfælde af en højere orden skal man ty til strukturanalyse og korrelationsmetoden .

Magisk firkantet struktur

Alle magiske firkanter har en intern struktur. Disse strukturer er forskellige afhængigt af firkantens rækkefølge og bliver mere og mere komplekse med stigende orden. For normale 4. orden magiske firkanter er der nøjagtigt 12 strukturgrupper med identiske parsummer. Disse kaldes også Dudeney -mønstre efter deres opdager Henry Dudeney . Billederne af strukturerne kan bruges til at analysere symmetriegenskaberne ved de magiske firkanter.

Særlige magiske firkanter

Generelle rigtige firkanter

Generelle reelle firkanter består af reelle tal . Deres eneste krav er, at rækker, kolonner og diagonaler udgør det samme beløb . Summen kan frit vælges. Generelle reelle firkanter er løsningen af ​​et homogent system af lineære ligninger . Systemet med ligninger har lineære ligninger. ${\ displaystyle s}$${\ displaystyle s}$${\ displaystyle 2n + 2}$

Eksempel på et resultat af den tredje ordens løsningssæt og : ${\ displaystyle s = 1.5}$

−0,5	2	0
1	0,5	0
1	−1	1.5

En enestående egenskab ved almindelige tredje-ordens reelle talkvadrater er, at det midterste talelement altid indeholder det aritmetiske middel for alle tal i firkanten. Det midterste talelement er derfor ikke kun middelværdien fra det rumlige begreb , men også fra det numeriske begreb på samme tid.

Hvis du som en yderligere betingelse angiver, at talfeltet kun består af naturlige tal , får du en endelig løsning angivet for hver målsum . Til 3. ordens firkanter og der er 25 løsninger (15 med og 10 uden gentagelse af tal). ${\ displaystyle s}$${\ displaystyle s = 27}$

14.	7.	6.
1	9	17.
12.	11	4.

Målsummen er en fri variabel af løsningssættet i det homogene lineære ligningssystem. Du kan derfor også bruge det beregnede magiske tal til måltotalen . Med det magiske nummer 15 får du 9 løsninger (8 med og 1 uden gentagelse af tal). Dette er Lo-Shu og hans domstol. ${\ displaystyle s}$${\ displaystyle s}$

Symmetriske magiske firkanter

Hvis en magisk firkant også opfylder betingelsen om, at summerne af to elementer, der er punktsymmetriske i forhold til midtpunktet (for lige) eller til det centrale element (for ulige magiske firkanter) er ens, kaldes det en symmetrisk magisk firkant . Det er mere præcist at bruge udtrykket centralt symmetrisk magisk firkant eller associativ magisk firkant . Som det let kan vises, skal summen af ​​to sådanne elementer være; for ulige symmetriske magiske firkanter har det midterste felt værdien . Symmetriske magiske firkanter har den enkleste indre struktur af de magiske firkanter. Den 3 x 3 magiske firkant er en symmetrisk magisk firkant. I tilfælde af de 4 x 4 magiske firkanter er kun en af ​​de 12 strukturelle grupper (gruppe 3) gruppen af ​​symmetriske magiske firkanter. Det er den stjerneformede repræsentation i strukturdiagrammerne. ${\ displaystyle n ^ {2} +1}$${\ displaystyle (n ^ {2} +1) / 2}$

I tilfælde af symmetriske magiske firkanter kan komplementet til startpladsen altid mappes på startpladsen ved at dreje den 180 °. det vil sige, at alle symmetriske magiske firkanter er selvkomplementerende (selvlignende).

Pandiagonal magiske firkanter

I tilfælde af en pandiagonal magisk firkant skal ikke kun summen af ​​diagonalerne, men også summen af ​​de knækkede diagonaler være den samme. De knækkede diagonaler løber parallelt med hoved- eller modsat diagonal , idet elementer uden for firkanten forskydes med en kantlængde. I modsætning til symmetriske magiske firkanter, i firkanter med en pandiagonal egenskab, kan denne særlige egenskab ikke altid læses direkte fra billedet af den interne struktur. Den mindste mulige rækkefølge for firkanter med en pandiagonal ejendom er 4. orden. Strukturgruppen 1 i 4. ordens firkanter består af de 48 pandiagonale firkanter. I tilfælde af magiske firkanter af en højere orden er der flere strukturelle grupper, der består af firkanter med pandiagonale egenskaber eller indeholder sådanne. De magiske firkanter i den symmetriske strukturelle gruppe af 5. orden har kun delvist den pandiagonale egenskab. Den symmetriske strukturelle gruppe er en strukturel hovedgruppe. For hovedstrukturgrupper er middelværdien i midten af ​​firkanten. Ved 5 gange 5 er dette værdien 13. Denne definition sikrer en uforvrænget repræsentation af den interne struktur. Hver ulige pandiagonal firkant kan bringes ind i en firkant af denne struktur ved at flytte den i skiftende klynge. Der er tre andre hovedstrukturgrupper i 5. orden, som består af pandiagonale firkanter. Disse uforvrængede strukturer er æstetisk tiltalende og viser den matematiske forbindelse mellem gennemsnit og symmetri. Ved at bevæge sig i forskydningsklyngen dannes de sekundære strukturgrupper for hver hovedstrukturgruppe.

Magiske firkanter, der er både symmetriske og pandiagonale, kaldes ultramagiske.

Magiske prime firkanter

Der er mange varianter af magiske firkanter, hvor kravet slippes, at kun tallene fra 1 til skal vises, men at yderligere betingelser skal være opfyldt. Den mest kendte af disse er magiske primtunker, hvor alle elementer skal være primtal (eller 1). ${\ displaystyle n ^ {2}}$

Tredje ordens magiske primtal med den mindste mulige magiske sum af 111 blev opdaget i 1900 af Henry Ernest Dudeney , der betragtede 1 som primtal. På det tidspunkt blev det anset for at være det første magiske primtal -kvadrat i løsningssættet med generelle magiske firkanter i 3. orden.

67	1	43
13	37	61
31	73	7.

Den første sande 3. orden magiske primtal har en mindste mulig magisk sum på 177.

17.	89	71
113	59	5
47	29	101

For første gang er der to forskellige magiske prime -firkanter for middelværdien 127 i løsningssættet med generelle magiske firkanter af 3. orden.

Antallet af normale magiske firkanter

Der er en (triviel) magisk firkant med kantlængde 1, men ingen med kantlængde 2. Bortset fra symmetrioperationer eller specificeret i Frénicle-standardformularen, er der kun en normal magisk firkant med kantlængde 3 (se under Lo-Shu ) . Alle 880 magiske firkanter med kantlængde 4 blev fundet af Frénicle de Bessy allerede i 1693. Med kantlængde 5 er der 275.305.224 magiske firkanter; endvidere kendes ingen nøjagtige tal, men der er relativt pålidelige skøn til og med ca. De mest omfattende beregninger blev udført af Walter Trump. Antallet af symmetriske, pandiagonale og ultramagiske firkanter for mindre er også kendt, for eksempel er der 48 symmetriske magiske firkanter med kantlængde 4 og 16 ultramagiske firkanter med kantlængde 5. ${\ displaystyle n = 20}$${\ displaystyle n}$

Berømte eksempler

Lo-Shu

Et eksempel er den ældste kendte magiske firkant fra Kina omkring 2800 f.Kr. I Europa var det i 16./17. Århundrede Saturn sæl ( Heinrich Cornelius Agrippa von Nettesheim , ca. 1510 og Athanasius Kircher , Arithmologia 1665) kaldet.

4.	9	2
3	5	7.
8.	1	6.

Lo-Shu er den eneste normale 3 x 3 magiske firkant.

Albrecht Dürer magiske firkant

En af de mest berømte magiske pladser i Albrecht Dürer's gravering Melancholia finder jeg .

16	3	2	13
5	10	11	8.
9	6.	7.	12.
4.	15.	14.	1

ejendomme

Dürer -pladsen har følgende egenskaber:

• Det er en symmetrisk magisk firkant.

Normale symmetriegenskaber ved magiske firkanter 4 x 4:

• Summen af ​​tallene i lodrette eller vandrette rækker er altid 34.
• Summen af ​​de to midterste diagonaler er 34 hver.
• Summen af ​​de fire hjørnefelter og de fire midterfelter er 34 hver.
• Summen af ​​de fire modstående centrale kantfelter er 34 hver ( og ).${\ displaystyle 5 + 9 + 8 + 12}$${\ displaystyle 3 + 2 + 15 + 14}$

Yderligere symmetriegenskaber ved Dürer -pladsen:

• Summen af ​​de to diagonaler, der er brudt i midten, er 34 hver ( og ).${\ displaystyle 3 + 5 + 12 + 14}$${\ displaystyle 2 + 8 + 9 + 15}$
• Summen af ​​elementerne i de fire kvadranter er 34 hver.
• Summen af ​​de fire felter, der hver modregnes med 1 eller 2 med uret fra de fire hjørnefelter, er 34 ( og ).${\ displaystyle 8 + 14 + 9 + 3}$${\ displaystyle 12 + 15 + 5 + 2}$
• Summen af ​​de to første tal i en række (f.eks. Den første) og de sidste to af den spejlede (f.eks. Den sidste) række (f.eks. ) Resulterer i 34. Dette gælder også tilsvarende kolonner (f.eks. ).${\ displaystyle 16 + 3 + 14 + 1}$${\ displaystyle 3 + 10 + 7 + 14}$
• Tallene i de to midterste rækker eller kolonner i zigzag -rækkefølge tilføjer op til 34 (f.eks. Eller ). Det samme gælder også for de to ydre rækker eller kolonner (f.eks. ).${\ displaystyle 3 + 11 + 6 + 14}$${\ displaystyle 9 + 10 + 7 + 8}$${\ displaystyle 16 + 8 + 9 + 1}$
• Summen af ​​hvert par, der er symmetrisk omkring midten, er 17. Dette svarer til det tredje Dudeney -mønster.

På grund af de yderligere symmetriegenskaber ved Dürer -pladsen kan to kvadrater genereres ved hjælp af udvekslingsoperationer. Ved at bytte kolonne 2 med kolonne 3 opstår kvadratet:

16	2	3	13
5	11	10	8.
9	7.	6.	12.
4.	14.	15.	1

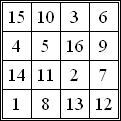
Denne dobbelte firkant har identiske symmetriegenskaber. Det svarer til torvet i Yang Hui . Selv Adam Ries brugte denne firkant i sin regnebog. Det er vist spejlet på hoveddiagonalen i begyndelsen af ​​artiklen.

En anden bytteoperation er swap af kolonner 1 med 2 og samtidig (16 swap) af kolonner 3 med 4. En 8 swap -operation er swap af to diagonale kvadranter (blokke med 4), f.eks. B. fra kvadrant 1 til kvadrant 3. Der er 12 muligheder for en 8-vejs swap-operation. Skiftet mellem de fire kvadranter til fire rækker er også en 8-vejs swap. Hjørnefelterne bliver hoveddiagonalen og kerneblokens felter bliver den modsatte diagonal. Den nye magiske firkant har ikke længere et match mellem summenes sammensætning (rækker, kolonner, diagonaler) og startpladsen. Bytteoperationen fra kvadranter til rækker danner grundlaget for beviset på, at summen af ​​elementerne i den respektive kvadrant i den centralt symmetriske firkant 4 gange 4 også er det magiske tal 34.

Disse udvekslingsoperationer er kun mulige med centralt symmetriske magiske firkanter 4 x 4. De nye magiske firkanter, der er oprettet med dem, kan stadig behandles med udvekslingsoperationer. Ved at kæde de nævnte udvekslingsoperationer kan alle 48 centralt symmetriske magiske firkanter (4 × 4) genereres. Forbindelsen kan repræsenteres ved hjælp af et tilstandsovergangsdiagram .

Fortolkninger

• I midten af ​​den sidste linje vises året 1514, året hvor Dürer lavede graveringen.
• I begyndelsen af ​​den sidste linje er der en 4, i slutningen en 1. Hvis du sidestiller disse tal med bogstaver i alfabetet, får du D og A, kunstnerens monogram (Dürer Albrecht)

De magiske firkanter fra det 16. og 17. århundrede i Europa

I den 16./17. Century begyndte en intensiv besættelse med magiske firkanter. Polymaterne Heinrich Cornelius Agrippa von Nettesheim og Athanasius Kircher udviklede flere magiske firkanter af en højere (op til 9 x 9) orden. Algoritmer til oprettelse af lige og ulige magiske firkanter er også blevet givet i værkerne. Tildelingen af ​​bestemte magiske firkanter til stjerner går tilbage til Agrippa. Jupiter -pladsen i Agrippa er identisk med Yang Huis 4 x 4 -firkant . De magiske firkanter med betegnelsen / tildelingen til stjerner blev brugt på mange amuletter.

Det magiske torv ved Sagrada Família

Facaden på Sagrada Família i Barcelona , dedikeret til lidenskaben , af billedhuggeren Josep Maria Subirachs , indeholder en magisk firkant:

1	14.	14.	4.
11	7.	6.	9
8.	10	10	5
13	2	3	15.

Det er ikke en magisk firkant i streng forstand, for ikke alle tal fra 1 til 16 vises (12 og 16 mangler), mens 10 og 14 vises to gange. Det magiske tal er 33, en hentydning til Kristi alder. Nummerpladsen på Sagrada Família kan genereres ved at trække 1 fra 4 elementer fra Dürer -pladsen. Værdierne for 12 elementer stemmer derfor overens med Dürer -pladsen. De 4 ændrede elementer blev valgt, så alle rækker, kolonner, diagonaler og blokke / kvadranter hver kan nås én gang.

Elementer på Dürer's square, fra hvis værdi 1 trækkes fra:

• e [1, 1] = 16
• e [2, 3] = 11
• e [3, 4] = 12
• e [4, 2] = 15

Drej den derefter 180 °. Subtraktionen af ​​de 4 elementer forårsager en strukturel ændring. Pladsen ved Sagrada Família er ikke centralt symmetrisk. Den har en bipolar struktur, dvs. dvs. summen af ​​de modstående elementer er 16 eller 17.

Goethes Hexeneinmaleins

Der er mange fortolkninger af Hexeneinmaleins fra Goethes Faust . Udover antagelsen om, at det simpelthen er nonsens, blev det også fortolket som en konstruktionsguide til et magisk kvadrat - en fortolkning, der ikke er hundrede procent overbevisende.

Konstruktion af magiske firkanter

Der er forskellige metoder til at konstruere magiske firkanter, som afhænger af kantens længde. Den enkleste metode, kaldet den siamesiske metode eller De-la-Loubère-metode, fungerer for alle magiske firkanter med ulige kantlængder (dvs. 3 × 3, 5 × 5, 7 × 7 osv.). Du starter øverst i midten med 1 og udfylder derefter de andre tal efter hinanden i henhold til følgende regel:

Hvis det sidste tal, der er skrevet, ikke er et multiplum af n, skal du indtaste det næste tal i feltet øverst til højre i det sidste udfyldte felt. Hvis det sidste tal, der er skrevet, er et multiplum af n, skal du indtaste det næste tal i feltet under det sidste skrevne tal. Hvis du forlader firkanten opad i henhold til disse regler, skal du skrive det næste tal helt nederst i kolonnen til højre for den kolonne, hvor det sidste tal blev skrevet. Hvis firkanten er venstre til højre, skal du skrive det næste tal længst til venstre i linjen, der er over linjen for det sidste skrevne tal.

Her betragtes den magiske firkant som periodisk gentaget; Det vil sige, at hvis du går over den øverste kant (dette sker med det første trin), kommer du tilbage nedenfra, og hvis du går ud til højre, kommer du tilbage fra venstre. Her er en 7 × 7 firkant konstrueret i henhold til denne regel:

30.	39	48	1	10	19.	28
38	47	7.	9	18.	27	29
46	6.	8.	17.	26	35	37
5	14.	16	25.	34	36	45
13	15.	24	33	42	44	4.
21	23	32	41	43	3	12.
22.	31	40	49	2	11	20.

Baseret på den siamesiske metode kan yderligere magiske firkanter med dobbelt orden genereres ved hjælp af LUX -metoden af John Horton Conway .

To andre metoder er for firkanter med en jævn kantlængde, en for alle firkanter, hvis kantlængde er delelig med 4, den anden for dem, hvor resten forbliver 2, når det divideres med 4.

En legende metode til konstruktion af magiske firkanter med lige ordrer større end 4 er mulig ved hjælp af Medjig -løsninger. Til dette har du brug for brikkerne i Medjig -puslespillet. Disse er firkanter fordelt på fire kvadranter, hvor prikker angiver tallene 0, 1, 2 og 3 i forskellige arrangementer. Puslespillet har 18 brikker, og der er tre forskellige arrangementer. Se billedet herunder. Målet med puslespillet er tilfældigt at tage 9 firkanter fra samlingen og placere denne underenhed i en 3 × 3 firkant, så der i hver række, kolonne og diagonal er i alt 9 (punkter).

Konstruktionen af ​​en magisk firkant af orden 6 ved hjælp af Medjig -puslespillet går som følger: Lav en 3 × 3 Medjig -løsning, denne gang kan du vælge ubegrænset fra den samlede samling. Derefter tager du den velkendte klassiske magiske firkant af orden 3 og deler alle firkanterne i fire kvadranter. Udfyld derefter kvadranterne med det originale nummer og de tre afledte modulo 9 -tal op til 36 efter Medjigs løsning. Den oprindelige felt med nummer 8 er således opdelt i fire områder med tallene , , og , feltet med tallet 3, 3, 12, 21 og 30, osv.; se eksempel herunder. ${\ displaystyle 8 \ (= 8 + 0 \ cdot 9)}$${\ displaystyle 17 \ (= 8 + 1 \ cdot 9)}$${\ displaystyle 26 \ (= 8 + 2 \ cdot 9)}$${\ displaystyle 35 \ (= 8 + 3 \ cdot 9)}$

8.   8.   3   3   4.   4.   8.   8.   3   3   4.   4.   1   1   5   5   9   9   1   1   5   5   9   9   6.   6.   7.   7.   2   2   6.   6.   7.   7.   2   2

+ 9 *

=

26   35   3   21   4.   22.   17.   8.   30.   12.   31   13   28   10   14.   23   27   9   1   19.   5   32   36   18.   33   24   25.   7.   2   20.   6.   15.   34   16   11   29

Du kan oprette 8. orden magiske firkanter på samme måde. Opret først en 4 × 4 Medjig -løsning (summen af ​​punkterne i hver række, kolonne, diagonal 12), og forstør derefter z. B. Dürers 4 × 4 firkant vist ovenfor modulo 16 til 64. Generelt er der brug for flere sæt Medjig -dele for at konstruere magiske firkanter af størrelsesordenen større end 9 på denne måde. For ordre 12 kan en 3 × 3 Medjig -løsning fordobles vandret og lodret, og derefter kan den 6 × 6 firkant, der er konstrueret ovenfor, udvides modulo 36 til 144. Det samme gælder for ordre 16.

Magiske firkanter i størrelsen 4 × 4 med det magiske tal kan konstrueres ved hjælp af følgende skema, hvor variablerne og står for eventuelle hele tal: ${\ displaystyle S}$${\ displaystyle a}$${\ displaystyle b}$

Generel ordning a + b -en 12a 7a 11a 8a b 2a 5a 10a 3a 3a + b 4a 2a + b 6a 9a

S = 34; a = 1, b = 13 14. 1 12. 7. 11 8. 13 2 5 10 3 16 4. 15. 6. 9

S = 88; a = 3, b = 25 28 3 36 21 33 24 25. 6. 15. 30. 9 34 12. 31 18. 27

Det magiske tal er hver . Skal z. B. være værdien 88, du trækker et heltalsmultiple på 21, resten er så tallet . : For eksempel (som vist i den højre firkant) . ${\ displaystyle S}$${\ displaystyle 21a + b}$${\ displaystyle S}$${\ displaystyle (= a)}$${\ displaystyle b}$${\ displaystyle 88-3 \ cdot 21 = 25}$

Magiske firkanter af denne type består generelt ikke af tallene 1, 2, 3,…, 16, og hvis værdierne ikke er valgt godt, og to felter kan indeholde det samme tal. Det magiske tal er ikke kun indeholdt i rækker, kolonner og diagonaler, men også i de fire kvadranter, i de fire hjørnefelter og i den lille firkant af de fire indre felter. ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle 21a + b}$

diverse

De magiske 4 × 4 firkanter, hvori kvadranterne også giver den magiske sum, kan - hvis man undværer den egenskab, at hvert af tallene fra 1 til 16 skal vises nøjagtigt én gang - som en lineær kombination af de følgende otte genererer, indbyrdes kongruente firkanter er repræsenteret:

Firkant A. 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 0	Firkant B 0 1 0 0 0 0 0 1 0 0 1 0 1 0 0 0	Firkant C 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0	Firkant D 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1
Firkant E. 0 0 0 1 1 0 0 0 0 0 1 0 0 1 0 0	Firkant F. 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 1	Firkant G 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0	Firkant H. 1 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0

Bemærk, at disse otte genererende firkanter ikke er lineært uafhængige pga

${\ displaystyle {A} + {D} + {E} + {H} = {B} + {C} + {F} + {G},}$

d. det vil sige, at der er en ikke-triviel lineær kombination (en lineær kombination, hvis koefficienter ikke alle er = 0), der giver 0-kvadratet. Med andre ord: hver af de otte genererende firkanter kan repræsenteres som en lineær kombination af de resterende syv. Syv genererende firkanter er nødvendige for at generere alle magiske 4 × 4 firkanter med den ekstra egenskab "Quadrants"; den vektorrum af de 4 x 4 magisk kvadrat genereres af disse kvadrater er 7-dimensionelle i denne forstand . Det er bemærkelsesværdigt, at i alle otte genererende firkanter A - H, som i Albrecht Dürer's magiske firkant, leverer ikke kun rækker, søjler og diagonaler altid den samme sum (1), men også hver af de fire "kvadranter", de fire centrale felter og de fire hjørnefelter. Dette betyder, at alle magiske firkanter, som vi får som lineære kombinationer af disse generatorer, har denne egenskab. Sammenhængen mellem de genererende firkanter muliggør z. B. at generere fra A ved rotation F, E og G og fra dette D, B, H og C ved spejling.

Den magiske firkant fra kobberstik Melencolia I af Albrecht Dürer som en lineær kombination af de frembringende firkanter A - G:

${\ displaystyle X = -4 \ cdot {A} +8 \ cdot {B} +14 \ cdot {C} -5 \ cdot {D} -1 \ cdot {E} +6 \ cdot {F} +16 \ cdot {G}}$

Summen af ​​koefficienterne er naturlig . ${\ displaystyle 34 = -4 + 8 + 14-5-1 + 6 + 16}$

At de 4 kvadranter også resulterer i den magiske sum, behøver ikke nødvendigvis at være tilfældet. Den følgende magiske firkant har ikke denne egenskab og er derfor lineært uafhængig af firkanterne A - H:

1	2	15.	16
13	14.	3	4.
12.	7.	10	5
8.	11	6.	9

Hvis du tilføjer denne firkant til 7 af firkanterne A-H, får du et grundlag for det 8-dimensionelle vektorrum for alle magiske 4 × 4 firkanter. Summen af ​​hjørnerne og de fire midterfelter er også den magiske sum for denne firkant (som med alle magiske 4 × 4 firkanter).

Bogstavfirkanter

En magisk bogstavfirkant er en hjerne -teaser med de samme ord i firkantenes rækker og kolonner. Et eksempel på dette er sator -firkanten :

S.	EN.	T	O	R.
EN.	R.	E.	P.	O
T	E.	N	E.	T
O	P.	E.	R.	EN.
R.	O	T	EN.	S.

Nummerpuslespil

Er nummerpuslespil arrangeret i firkanter

• Mazara
• Sudoku

Yderligere emner

• Magic Cube , en tredimensionel udvidelse af magiske firkanter
• Magisk sekskant , et arrangement af tal i en bikageform
• Perfekt perfekt magisk firkant , magiske firkanter med ekstra egenskaber ved underkanterne
• Magisk lyd firkantet
• Magisk graf

Supplerende litteratur

• Jacques Sesiano: Fremstillingsproces af magiske firkanter fra islamisk tid. I-III. I: Sudhoffs arkiv. Bind 64, 1980, nr. 2, s. 187-196; Bind 65, 1981, nr. 3, s. 251-256; Bind 71, 1987, nr. 2, s. 78-89; Bind 79, 1995, nr. 2, s. 192-226.
• Siegmund Günther: Blandede undersøgelser af de matematiske videnskabers historie. Forlag Teubner Leipzig, 1876, kap. IV, Historiske studier af magiske firkanter
• Wolfgang Göbels: Varianter af den magiske firkant af Albrecht Dürer. I: Practice of Mathematics (PM) 4/35. Født i 1993, Aulis Verlag

Weblinks

• Dybdegående artikler om magiske firkanter
• Siden af ​​kunstneren Paul Heimbach, Köln
  • Historie
• Siden er ikke længere tilgængelig , søg i webarkiver: Dürer's magiske firkant og dens betydning i Thomas Manns Doctor Faustus@1@ 2Skabelon: Toter Link / www.heim2.tu-clausthal.de
• Christoph Pöppe: Ædle magiske firkanter. Nogle magiske firkanter har en intern struktur, der gør det muligt at lave en enkelt magisk firkant til mange andre. I: Spektrum der Wissenschaft 1. 1996, s. 14 , åbnet den 28. februar 2012 . 
• Betragtning af magiske firkanter med forklaringer om sumkombinationerne på den magiske firkant af Albrecht Duerer

Individuelle beviser

1. ↑ Holger Danielsson: Magiske firkanter , side 77 ff.
2. ↑ Magiske firkanter. På: mathe-online.at. (PDF).
3. ^ Hans-Wolfgang Henn, Andreas Filler: Didactics of Analytical Geometry and Linear Algebra, Springer Spectrum, sider 129-134
4. ↑ Eric W. Weisstein : Prime Magic Square . I: MathWorld (engelsk).
5. ↑ ^{a b c d} Korrespondancekreds MATEMATIK - LSGM, nummer 06/2003, PDF. S. 4.
6. ↑ Martin Gardner : Matematisk labyrint: Nye problemer for Knobelgemeinde . Vieweg Verlag , Braunschweig / Wiesbaden 1979, ISBN 978-3-528-08402-8 , s. 87 , doi : 10.1007 / 978-3-322-83962-6_9 . 
7. ^ Optælling af magiske firkanter. På: trump.de.
8. ^ Philos-Spiele, art.nr. 6343.