Kompleksitetsteori
Den kompleksitetsteori som en gren af teoretisk datalogi beskæftiger sig med den kompleksitet algoritmisk genstridige problemer på forskellige formelle computermodeller . Kompleksiteten af algoritmer måles i deres ressourceforbrug , normalt beregningstid eller behov for hukommelsesplads , undertiden også mere specifikke målinger såsom størrelsen på et kredsløb eller antallet af processorer, der kræves til parallelle algoritmer . Kompleksiteten af et problem er igen kompleksiteten af algoritmen, der løser problemet med mindst mulig ressourceforbrug.
Kompleksitetsteorien adskiller sig fra beregnelighedsteorien , der beskæftiger sig med spørgsmålet om, hvilke problemer der principielt kan løses algoritmisk. I modsætning hertil er det vigtigste forskningsmål for kompleksitetsteori at klassificere sættet med alle løselige problemer. Især forsøger man at afgrænse sæt af effektivt løselige problemer, hvis forbrug af ressourcer kan styres i praksis fra sæt af iboende vanskelige problemer.
Klassifikation i teoretisk datalogi
Kompleksitetsteori er sammen med beregnelighedsteori og teori om formelle sprog et af de tre hovedområder inden for teoretisk datalogi. Et af hendes vigtigste forskningsmål er klassificeringen af problemer med hensyn til den krævede indsats for at løse dem. Afgrænsningen af de praktisk effektivt løselige problemer spiller en særlig rolle. Kompleksitetsteori begrænser derfor de problemer, som andre discipliner inden for datalogi fornuftigt skal søge efter effektive løsninger, og motiverer således udviklingen af praktiske tilnærmelsesalgoritmer .
Ud over den rene gevinst i viden beriger metodearsenalet af kompleksitetsteoretisk forskning også adskillige tilstødende områder. For eksempel fører deres tætte sammenkobling med automatteori til nye maskinemodeller og en mere omfattende forståelse af, hvordan automater fungerer. De ofte konstruktive beviser bruges også i sammenhæng med design og analyse af algoritmer og datastrukturer .
Problemer ud fra kompleksitetsteoriens synspunkt
Beslutningsproblemer som formelle sprog
Det centrale emne for kompleksitetsteori er problemer , som regel beslutningsproblemer , hvis tilfælde kræver et ja / nej-svar. Et beslutningsproblem præsenteres ofte som formelt sprog . Hver forekomst af problemet udtrykkes som et ord over et alfabet; H. som en række af tegn fra dette alfabet. Det pågældende sprog består af de ord, som en instans med svaret "ja" svarer til. Opgaven består derefter i at løse ordproblemet , dvs. at beslutte for et givet ord, om det hører til sproget eller ej, og med det har man også fundet svaret på den tilsvarende probleminstans.
For eksempel, hvis problemet er at afgøre, om en graf sammenhængende eller ej, så vil et ord være en repræsentation af en hvilken som helst graf . Det tilknyttede afgørende sprog ville være det sæt af ord, der repræsenterer en sammenhængende graf.
Man kan antage, at begrænsningen til beslutningsproblemer udelukker mange vigtige problemer. Der er dog også et tilsvarende beslutningsproblem for alle problemer, der er relevante i betydningen af kompleksitetsteori. Hvis man for eksempel overvejer problemet med multiplikation af to tal, består det tilknyttede sprog i beslutningsproblemet af alle tredobler af tal, som forholdet gælder for. At beslutte, om en given tredobbelt tilhører dette sprog, svarer til at løse problemet med at multiplicere to tal.
Beregningsproblemer som illustrationer
Ud over beslutningsproblemer overvejer man også beregningsproblemer. Dette kræver et svar, der beskriver løsningen på problemet. Multiplikationsproblemet præsenterer sig for eksempel normalt i praksis som et beregningsproblem: Du vil finde produktet med to tal.
Man forstår et beregningsproblem som en kortlægning fra et definitionsdomæne til et løsningsrum, i tilfælde af multiplikation af naturlige tal som en kortlægning . Et andet eksempel er det rejsende sælgerproblem . Her ser man efter den optimale rækkefølge, hvor man kan besøge givne steder, hvorved den samlede længde af ruten skal være minimal. Mange optimeringsproblemer er af stor praktisk betydning. Til definitionen af de fleste af kompleksitetsklasser foretrækkes formuleringen med hensyn til beslutningsproblemer.
Optimeringsproblemerne repræsenterer en vigtig underkategori af beregningsproblemerne.I tilfælde af optimeringsproblemer består det funktionelle forhold af kravet om at bestemme maksimum eller minimum for en given omkostningsfunktion over alle mulige løsninger på problemet. I tilfælde af et rejsesælgerproblem skal længden af den optimale rute beregnes.
Problem tilfælde
En problemforekomst må ikke forveksles med selve problemet. I kompleksitetsteori repræsenterer et problem et generelt spørgsmål, en skabelon. En forekomst af problemet er derefter et komplet spørgsmål, der definerer det rigtige svar (ja eller nej i tilfælde af et beslutningsproblem).
Ét eksempel på det rejsende sælgerproblem kan f.eks. Være spørgsmålet om, hvorvidt der findes en rute gennem de tyske hovedstæder i Tyskland med en maksimal længde på 2000 km. Beslutningen om at tage denne rute har dog begrænset værdi for andre tilfælde af problemet, såsom en rundvisning i seværdighederne i Milano . I kompleksitetsteori er man derfor interesseret i udsagn, der er uafhængige af specifikke tilfælde.
Et problem er formuleret på en så generel måde, at det definerer et uendeligt sæt problemforekomster, fordi det ikke giver mening at spørge om kompleksiteten af et endeligt sæt forekomster; et program kunne indeholde en liste med færdige svar og kun returnere den rigtige løsning ved at få adgang til en tabel, der ikke afspejler den krævede indsats for at bestemme svarene. Det bliver kun interessant, når der er et uendeligt antal forekomster, og du vil finde en algoritme, der beregner det rigtige svar for hver forekomst.
Problemrepræsentationer
Som formelle sprog defineres problemer og deres forekomster ved hjælp af abstrakte alfabeter . Det binære alfabet med symbolerne 0 og 1 vælges ofte, da dette kommer tættest på brugen af bits i moderne computere. Indgange kodes derefter ved hjælp af alfabetssymboler. I stedet for matematiske objekter, såsom grafer, kan der anvendes en bitfølge, der svarer til grafens tilstødningsmatrix i stedet for naturlige tal, for eksempel deres binære repræsentation .
Selvom bevis for kompleksitetsteoretiske udsagn normalt bruger konkrete repræsentationer af inputet, forsøger man at holde udsagn og overvejelser uafhængige af repræsentationer. Dette kan f.eks. Opnås ved at sikre, at den valgte repræsentation om nødvendigt kan omdannes til en anden repræsentation uden for meget indsats, uden at den samlede beregningsindsats ændres væsentligt som et resultat. For at gøre dette muligt er det blandt andet vigtigt at vælge en passende universel maskinemodel.
Problemstørrelse
Når først et problem er defineret formelt (for eksempel den rejsende sælgers problem i form af en graf med kantvægte), vil man gerne komme med udsagn om, hvordan en algoritme opfører sig, når man beregner problemløsningen afhængigt af problemets vanskelighed. Generelt er der mange forskellige aspekter, der skal overvejes i vurderingen af problemets sværhedsgrad. Ikke desto mindre er det ofte muligt at finde nogle få skalarmængder, der i væsentlig grad påvirker algoritmens opførsel med hensyn til ressourceforbrug. Disse størrelser er kendt som problemstørrelsen. Dette svarer som regel til inputlængden (i tilfælde af en specifikt valgt repræsentation af input).
Man undersøger nu algoritmens opførsel som en funktion af problemstørrelsen. Kompleksitetsteorien er interesseret i spørgsmålet: Hvor meget ekstra arbejde er nødvendigt for at øge problemstørrelser? Stiger indsatsen (i forhold til problemstørrelsen) lineært , polynomielt , eksponentielt eller endda overeksponentielt?
I tilfælde af et rejsesælgerproblem kan f.eks. Problemstørrelsen defineres som antallet af givne placeringer (forsømmelse af at de givne rute længder også kan have inputvariabler i forskellige størrelser). Så er dette problem trivielt for problemstørrelse 2, da der kun er en mulig løsning her, og det derfor også skal være optimal. Når problemstørrelsen stiger, bliver en algoritme dog nødt til at udføre mere arbejde.
Bedste, værste og gennemsnitlige tilfælde for problemstørrelser
Selv inden for en problemstørrelse kan forskellig opførsel af algoritmer observeres. Problemet med den rejsende sælger for de 16 tyske hovedstæder har samme problemstørrelse som at finde en rute gennem 16 europæiske hovedstæder. Det kan på ingen måde forventes, at en algoritme fungerer lige så godt under de forskellige forhold (selv med den samme problemstørrelse). Men da der normalt er et uendeligt antal forekomster af samme størrelse for et problem, er de normalt groft grupperet i tre grupper: bedste, gennemsnitlige og værste tilfælde. Disse står for spørgsmålene:
- Bedste tilfælde: Hvordan fungerer algoritmen (i forhold til den pågældende ressource) i bedste fald?
- Gennemsnitlig sag: Hvordan fungerer algoritmen i gennemsnit (skønt den underliggende fordeling til beregning af et gennemsnit ikke altid er åbenbar)?
- Amortiseret tilfælde: Hvordan fungerer algoritmen i værste fald for en række kørsler?
- Værste tilfælde: hvordan fungerer algoritmen i værste fald?
Funktionerne i resultaterne af spørgsmålene er ordnet i stigende rækkefølge, hvis de er tydeligt angivet, dvs. Dette betyder: et problem, der er afskrevet, for eksempel kvadratisk efterspørgsel, har (højst) kvadratisk efterspørgsel også i gennemsnit og i værste fald ikke mindre.
Nedre og øvre grænse for problemer
Overvejelsen af de bedste, værste og gennemsnitlige tilfælde vedrører altid en fast inputlængde. Selv om hensynet til specifikke inputlængder kan være af stor interesse i praksis, er denne opfattelse normalt ikke abstrakt nok til kompleksitetsteori. Hvilken inputlængde, der betragtes som stor eller praktisk relevant, kan ændre sig meget hurtigt på grund af den tekniske udvikling. Det er derfor berettiget at undersøge algoritmernes opførsel i forhold til et problem helt uafhængigt af specifikke inputlængder. Til dette formål betragter man algoritmernes opførsel for stadigt stigende, potentielt uendeligt store inputlængder. Man taler om den asymptotiske opførsel af den respektive algoritme.
I denne undersøgelse af det asymptotiske ressourceforbrug spiller nedre og øvre grænser en central rolle. Så du vil vide, hvilke ressourcer der mindst er nødvendige for at løse et problem. De nedre grænser er af særlig interesse for kompleksitetsteori: Man vil gerne vise, at et bestemt problem kræver mindst en vis mængde ressourcer, og der kan derfor ikke være nogen algoritme, der bestemmer problemet med færre ressourcer. Sådanne resultater hjælper med at adskille problemer med hensyn til deres vanskeligheder på lang sigt. Imidlertid er der indtil videre kun relativt få meningsfulde nedre grænser kendt. Årsagen til dette ligger i problemet, at undersøgelser af lavere grænser altid skal henvise til alle tænkelige algoritmer for et problem; således også på algoritmer, der ikke engang er kendt i dag.
I modsætning hertil opnås beviset for øvre grænser normalt ved at analysere specifikke algoritmer. Ved at bevise eksistensen af endog en algoritme, der overholder den øvre grænse, er beviset allerede leveret.
I tilfælde af visse problemer, såsom kompleksiteten af krypteringsmetoder , forsøges det at bevise, at det forventede forbrug af ressourcer, når man forsøger at bryde metoden, overstiger ethvert realistisk niveau. For problemer, der ikke kan løses, selv med en computer på størrelse med jorden under jordens levetid, blev udtrykket transcomputational problem opfattet.
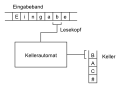
Maskinsmodeller i kompleksitetsteori
Omkostningsfunktioner
For at analysere ressourceforbruget af algoritmer skal der defineres egnede omkostningsfunktioner , som gør det muligt at tildele algoritmens arbejdstrin til de anvendte ressourcer. For at være i stand til dette skal det først bestemmes, hvilken type arbejdstrin der er tilladt for en algoritme. I kompleksitetsteori, er denne definition lavet ved hjælp af abstrakte maskine modeller - hvis der blev brugt rigtig computermodeller, ville den opnåede viden være forældet på få år. Arbejdstrinnet for en algoritme har form af udførelse af en kommando på en bestemt maskine. Kommandoerne, som en maskine kan udføre, er strengt begrænset af den respektive model. Derudover adskiller forskellige modeller sig for eksempel i håndtering af hukommelsen og i deres muligheder for parallel behandling, dvs. H. samtidig udførelse af flere kommandoer. Omkostningsfunktionen defineres nu ved at tildele omkostningsværdier til de kommandoer, der er tilladt i hvert enkelt tilfælde.
Omkostningsforanstaltninger
Ofte er forskellige omkostninger for forskellige kommandoer abstraheret, og 1 er altid indstillet som omkostningsværdien for kommandokørsel. For eksempel, hvis tilføjelse og multiplikation er de tilladte operationer på en maskine , tilføjes omkostningsværdien 1 for hver tilføjelse og hver multiplikation, der skal beregnes i løbet af algoritmen. Man taler derefter om et ensartet omkostningsmål . En sådan procedure er berettiget, hvis de tilladte operationer ikke adskiller sig væsentligt, og hvis rækkevidden af værdier, som operationerne arbejder på, kun er begrænset i størrelse. Dette bliver klart for en simpel operation som multiplikation: Produktet med to encifrede decimaltal skal beregnes meget hurtigere end produktet af to hundrede cifrede decimaltal. Med en ensartet omkostningsmåling vil begge operationer stadig have en omkostning på 1. Hvis de mulige operander faktisk adskiller sig så markant i løbet af en algoritme, skal der vælges et mere realistisk omkostningsmål. Ofte vælger man derefter det logaritmiske omkostningsmål . Henvisningen til logaritmen skyldes, at et decimaltal i det væsentlige kan repræsenteres af mange binære cifre. Binære cifre er valgt for at repræsentere operanderne, og de tilladte boolske operationer er defineret . Hvis den respektive maskinemodel bruger adresser, er disse også kodet i binær. På denne måde vægtes omkostningerne logaritmisk over længden af den binære repræsentation. Andre omkostningsforanstaltninger er mulige, men bruges sjældent.
Maskinsmodeller og problemer
Man skelner mellem forskellige beregningsparadigmer: Den mest pragmatiske type er bestemt den af de deterministiske maskiner; der er også den type ikke-deterministisk maskine, der er særlig relevant i teorien ; der er stadig sandsynlighedsmaskiner , alternerende og andre. Generelt kan enhver maskinemodel defineres ved hjælp af et af paradigmerne ovenfor. Nogle paradigmer, såsom ikke-bestemmelse, modellerer en type, der skal reserveres til teori, da ikke-bestemmelse ikke fysisk kan bygges i den form, der er defineret der (du kan "gætte" en korrekt sti i et beregningstræ ), men det er ofte let at konstruere til et givet problem. Da en transformation fra ikke-deterministisk til deterministisk maskine altid er relativt let, konstruerer man derfor først en ikke-deterministisk maskineversion og senere omdanner den til en deterministisk.
Heraf fremgår en vigtig bevisteknik for kompleksitetsteori: Hvis en bestemt maskintype kan konstrueres til et givet problem, hvorpå problemet kan løses med visse omkostninger, kan problemets kompleksitet allerede estimeres. Faktisk bruges selv de forskellige maskinmodeller som grundlag for definitionen af kompleksitetsklasser . Dette svarer til en abstraktion fra en konkret algoritme: Hvis der kan afgøres et problem på maskinen (selvom en tilsvarende algoritme måske ikke engang er kendt), kan den tildeles direkte til en bestemt kompleksitetsklasse, nemlig den, der er defineret af. Denne sammenhæng mellem problemer og maskinmodeller gør det muligt at udarbejde beviser uden den besværlige analyse af algoritmer.
Ofte anvendte maskinmodeller
De mest almindelige modeller er:
For at undersøge problemer, der kan paralleliseres, kan der også anvendes parallelle versioner af disse maskiner, især parallelregistreringsmaskinen .
Den udvidede afhandling fra Church-Turing
Til brug af maskinmodeller i kompleksitetsteori er en udvidelse af Church-Turing-afhandlingen vigtig, som også er kendt som den udvidede Church-Turing-afhandling . Det siger, at alle universelle maskinemodeller er lige så effektive med hensyn til computingstid bortset fra polynomiske faktorer. Dette giver kompleksitetsteoretikeren et relativt frit valg af maskinmodellen med hensyn til det respektive forskningsmål. Denne afhandling kan heller ikke bevises; I modsætning til den sædvanlige afhandling fra Church-Turing ville det være muligt at afkræfte det med et modeksempel.
Modelændringer til analyse af lagerplads
For at undersøge de mindste hukommelseskrav, der kræves for at løse problemer, foretages ofte følgende ændringer af den anvendte maskinemodel (normalt en Turing-maskine):
- Indgangshukommelsen må kun læses .
- Outputtet kan kun skrives til. Skrivehovedet bevæges kun efter skrivning og altid i samme retning (hvis maskinmodellen tillader en sådan bevægelse).
Maskinens input og output kan derefter ses bort fra ved undersøgelsen af hukommelseskravet. Motivationen for disse ændringer er som følger: Hvis f.eks. Inputhukommelsen var inkluderet i hukommelsesanalysen , kunne intet problem løses i mindre end pladsbehov, fordi inputordet altid har den nøjagtige længde og dermed hukommelseskravet n gør det læsbart, forhindrer det, at det bruges til midlertidige fakturaer. Du kan derefter forsømme input, når du beregner pladsbehovet. En lignende begrundelse fører til begrænsningen af output. Den yderligere begrænsning af mulig bevægelse af hovedet forhindrer, at hovedpositionen bruges til at "huske" information. Samlet set sikrer alle disse begrænsninger, at input og output ikke skal tages i betragtning i lagerpladsanalysen.
De foretagne ændringer påvirker kun maskinens tidsadfærd med en konstant faktor og er derfor ubetydelige.
Landau notation
Når man undersøger størrelsesorden for indsats, anvender kompleksitetsteori i vid udstrækning Landau- eller O-notationen til at beskrive (minimum, gennemsnit eller maksimum) tid eller lagerpladsbehov for en algoritme. Man taler derefter om tidskompleksitet eller rumkompleksitet . Kompleksiteten kan afhænge af den maskinmodellen anvendte . Som regel antages der dog en “normal” model, for eksempel en, der svarer til Turing-maskinen . Ved at gøre dette er lineære faktorer og konstanter skjult for synspunktet. Denne tilgang kan komme som en overraskelse i starten, da det ofte ville være meget vigtigt for den praktiserende læge at halvere indsatsen.
Synspunktet for kompleksitetsteori kan teoretisk retfærdiggøres med en teknik kaldet lineær acceleration eller speed-up-sætningen . (Vi begrænser os her til tidsadfærd. Analoge beviser kan også gives for hukommelseskravet eller andre ressourcer.) Speedup-sætningen siger ganske enkelt, at for hver Turing-maskine, der beslutter et problem i tide , kan der konstrueres en ny Turing-maskine, der problemet er mindre end løst i tide . Det kan vælges så lille som ønsket. Det betyder intet andet end at hver Turing-maskine, der løser et bestemt problem, kan accelereres med en hvilken som helst konstant faktor. Prisen for denne acceleration består i en stærkt forøget alfabetstørrelse og tilstandssæt for den anvendte Turing-maskine (i sidste ende "hardware").
Denne acceleration opnås uanset størrelsen på problemet. Derfor, når man overvejer problemets asymptotiske opførsel, giver det ingen mening at overveje konstante faktorer - sådanne faktorer kan elimineres ved at anvende accelerationsteknikken. Forsømmelsen af konstante faktorer, der kommer til udtryk i O-notationen, har derfor ikke kun praktiske grunde, den undgår også forfalskninger i sammenhæng med kompleksitetsteoretiske overvejelser.
Det er ofte meget tidskrævende eller helt umuligt at specificere en funktion til et problem, der generelt tildeler det tilknyttede antal computertrin (eller hukommelsesceller) til enhver input til et problem. Derfor er du normalt i stedet for at indtaste hver enkelt input tilfreds med kun at begrænse dig til inputlængden . Det er dog normalt for tidskrævende at specificere en funktion .
Landau-notationen blev derfor udviklet, hvilket er begrænset til funktionens asymptotiske opførsel . Så du overvejer grænserne for beregningsindsatsen (behovet for hukommelse og computertid), når du forstørrer input. Det vigtigste Landau-symbol er (stort latinsk bogstav "O"), hvormed man kan angive øvre grænser ; lavere grænser er generelt meget sværere at finde. Her er (ofte ), at en konstant og eksisterer, således at der for alle gælder følgende: . Med andre ord: For alle inputlængder er beregningsindsatsen ikke signifikant større - dvs. H. højst med en konstant faktor - som .
Funktionen er ikke altid kendt; som en funktion vælges der dog normalt en funktion, hvis vækst er velkendt (såsom eller ). Landau-notationen er der for at estimere beregningsindsatsen (pladsbehov), hvis det er for tidskrævende at specificere den nøjagtige funktion, eller hvis den er for kompliceret.
Landau-symbolerne gør det muligt at gruppere problemer og algoritmer i kompleksitetsklasser alt efter deres kompleksitet .
I kompleksitetsteori kan de forskellige problemer og algoritmer derefter sammenlignes som følger: For problemer med kan man angive en nedre grænse for for eksempel den asymptotiske køretid med tilsvarende en øvre grænse. Ved , betegnes formen af (fx ) også kompleksitetsklassen eller mål for indsats (fx kvadratisk).
I denne notation, som definitionerne af Landau-symbolerne viser, forsømmes konstante faktorer. Dette er berettiget, fordi konstanterne i høj grad er afhængige af den anvendte maskinemodel eller, i tilfælde af implementerede algoritmer, af kompilatorens kvalitet og forskellige egenskaber ved hardwaren til den udførende computer . Dette betyder, at deres informative værdi om kompleksiteten af algoritmen er meget begrænset.
Oprettelse af kompleksitetsklasser
En væsentlig opgave med kompleksitetsteori er at bestemme meningsfulde kompleksitetsklasser , sortere de aktuelle problemer i disse og finde udsagn om de gensidige forhold mellem klasserne.
Påvirker variabler i dannelsen af kompleksitetsklasser
En række faktorer påvirker dannelsen af kompleksitetsklasser. De vigtigste er følgende:
- Den underliggende beregningsmodel (Turing-maskine, registermaskine osv.).
- Den anvendte beregningstilstand (deterministisk, ikke-deterministisk, probabilistisk osv.).
- Den beregningsressource, der overvejes (tid, rum, processorer osv.).
- Det antagne mål for omkostninger (ensartet, logaritmisk).
- Den anvendte barrierefunktion .
Krav til barrierefunktioner
At specificere eller definere kompleksitetsklasser ved hjælp af barrierefunktioner . For eksempel, hvis du skriver DTIME (f), mener du klassen af alle problemer, der kan løses på en deterministisk Turing-maskine i tide . er en barrierefunktion. For at kunne bruges som en barrierefunktion til kompleksitetsteoretiske analyser, skal funktionen mindst opfylde følgende krav:
- (Trinnummer, hukommelse osv. Beregnes som naturlige tal).
- (monoton vækst).
- Selve funktionen skal kunne beregnes med hensyn til tid og rum . (Rum / tid konstruktionsevne)
En funktion, der opfylder disse krav, kaldes også en reel kompleksitetsfunktion . Formålet med kravene er dels af teknisk art. Selve barrierefunktionen kan strømme ind i bevis på en konstruktiv måde (f.eks. Som en Turing-maskine) og bør derfor opføre sig "godartet" til disse formål. På dette tidspunkt skal det kun påpeges, at der skal udvises en vis forsigtighed, når du vælger barrierefunktionen, fordi ellers visse algoritmiske teknikker ikke kan bruges.
Fleste af de funktioner der forekommer i praksis svarer til de begrænsninger nævnt ovenfor, såsom den konstante funktion, den logaritmiske funktion , den kvadreringsfunktion , polynomier , den eksponentielle funktion og alle kombinationer af disse funktioner. Følgende er en oversigt over de vigtigste barrierefunktioner med den sædvanlige måde at tale på. Som normalt er det specificeret i O-notation .
De vigtigste barrierefunktioner
| konstant | |
| logaritmisk | |
| polylogaritmisk | Til |
| lineær | |
| linearitmisk | |
| firkant | |
| polynom | Til |
| eksponentielt | Til |
| Faktor |
Hierarki registreres
For de uddannede klasser vil man så vidt muligt bevise, at flere problemer faktisk kan løses med yderligere ressourcer . Disse bevis kaldes hierarkisæt (også kaldet separationssæt ), da de inducerer et hierarki over klasserne for den respektive ressource. Så der er klasser, der kan sættes i et ægte delmængdeforhold. Når sådanne reelle delmængderelationer er blevet bestemt, kan der også fremsættes udsagn om, hvor stor stigningen i en ressource skal være for at kunne beregne et større antal problemer. Ressourcerne for tid og rum er af særlig interesse. De inducerede hierarkier kaldes også tidshierarki og rumhierarki .
Hierarkisættene danner i sidste ende grundlaget for adskillelsen af kompleksitetsklasser. De udgør nogle af de tidligste fund i kompleksitetsteorien. Det skal tilføjes, at alle hierarkiposter er baseret på forskellige krav. En af disse forudsætninger er for eksempel, at de ovennævnte krav til reelle kompleksitetsfunktioner er opfyldt. Hvis disse krav ikke er opfyldt, kollapser hele klassehierarkiet.
Tidshierarki indstillet
I tidshierarkiets sætning hedder det:
Så der er problemer, hvis asymptotiske tidskrav til en deterministisk Turing-maskine inden for klassen ikke er i . Et lignende forhold kan findes for ikke-deterministiske Turing-maskiner.
Rumhierarki sæt
Den rumlige hierarki sætning siger:
Erklæringen er analog med tidshierarkiets sætning. Man erkender dog, at sammenlignet med den tid, der allerede er, er en mindre pladsforøgelse tilstrækkelig (faktor sammenlignet med ) til at danne en større klasse. Dette svarer også til en intuitiv forventning, da rummet som helhed opfører sig mere godmodig på grund af dets genanvendelighed (gamle midlertidige resultater kan overskrives).
Hvad hierarkiposterne ikke gælder for
Hierarkiposterne vedrører udelukkende den samme beregningstilstand og en enkelt ressource, for eksempel tidsressourcen på en deterministisk maskinemodel. Imidlertid fremsættes der ingen erklæringer om, hvordan rum- og tidsklasser relaterer til hinanden eller forholdet mellem deterministiske og ikke-deterministiske klasser. Ikke desto mindre er der forbindelser af denne art. De er dækket af afsnittene Forholdet mellem rum- og tidsklasser og forholdet mellem deterministiske og ikke-deterministiske klasser .
Vigtige tidskurser
- DTIME (f): Generel notation for deterministiske tidsklasser .
- P : Sprog, der bestemmes deterministisk i polynomisk tid.
- EKSPTID : Sprog, der kan bestemmes deterministisk i eksponentiel tid.
- NTIME (f): Generel notation for ikke-deterministiske tidsklasser .
- NP : Sprog, der ikke kan bestemmes deterministisk i polynomisk tid.
- NÆSTE TID : Ikke-bestemmelsesmæssigt bestemte sprog i eksponentiel tid.
- NC : Funktioner, der kan beregnes parallelt i polylogaritmisk tid.
Vigtige rumklasser
- DSPACE (f): Generel notation for deterministiske rumklasser .
- L : Sprog, der bestemmes deterministisk med logaritmisk begrænset plads.
- PSPACE : Bestemmeligt bestemte sprog med polynomisk afgrænset plads.
- NSPACE (f): Generel notation for ikke-deterministiske rumklasser .
- NL : Ikke-bestemmelsesmæssigt bestemte sprog med logaritmisk begrænset plads.
- CSL : Kontekstfølsomme sprog er de ikke-deterministisk afgørelige sprog med lineært begrænset plads.
Se også: Liste over kompleksitetsklasser
Komplementering
For hver kompleksitetsklasse K kan dens komplementklasse CoK dannes: Komplementklassen indeholder nøjagtigt komplementerne til elementerne i den originale klasse. Hvis man forstår K som et sæt sprog ( se power set ), så er det komplementklassen . I forhold til de tilsvarende beslutningsproblemer betyder dette: CoK indeholder de problemer, hvis tilfælde svaret altid er det modsatte af et problem i K.
I modsætning hertil kan man også overveje komplementet til en klasse K. Dette indeholder nøjagtigt de sprog / problemer fra et givet basissæt, der ikke er i K; disse problemer er normalt meget mere alvorlige end dem i K. Komplementklassen CoK har derimod normalt et ikke-tomt gennemsnit med K.
Som regel gælder K = CoK for deterministiske maskiner, da i overgangsfunktionen kun de overgange, der skal accepteres, skal udveksles for at overgange skal afvises og omvendt. Dette gælder dog ikke andre beregningstilstande, da accept er defineret forskelligt her . For eksempel vides det endnu ikke, om NP = CoNP gælder. P = CoP er sandt, fordi den underliggende model er deterministisk, og her kan de accepterende og afvisende stater simpelthen udveksles i beregningerne, som nævnt i det foregående afsnit. Så vi ser straks, at P er indeholdt i skæringspunktet mellem NP og CoNP. Det vides ikke, om dette gennemsnit er nøjagtigt P.
P-NP-problemet og dets betydning
Et af de vigtigste og stadig uløste problemer i kompleksitetsteori er P-NP-problemet . Er klasse P lig med klasse NP ? Dette spørgsmål kan ses som en central motivation for forskning i kompleksitetsteori, og et stort antal af kompleksitetsteoretiske resultater blev opnået for at komme tættere på at løse P-NP-problemet.
Klasse P: Praktisk løselige problemer
Omfanget af P-NP-problemet skyldes erfaringen med, at problemerne i klasse P normalt er praktisk løselige: der findes algoritmer til at beregne løsninger på disse problemer effektivt eller i det mindste med en rimelig tidsforbrug. Den tid, der kræves til at løse problemet, vokser mest for problemerne med klasse P polynom . Som regel kan algoritmer findes, hvis tidsfunktioner er lavgradige polynomer . Da den valgte maskinemodel i denne tidsklasse er deterministisk (og dermed realiserbar), svarer problemerne i klasse P nogenlunde til de praktisk løselige problemer, selvom man betragter tilfælde af betydelig størrelse.
Klassen NP: effektivt verificerbare problemer
Algoritmerne til løsning af problemerne i NP er baseret på en ikke-deterministisk maskinemodel . For sådanne maskiner forudsættes ubegrænset parallelisering af forgreningsberegningsstierne, som ikke kan implementeres teknisk. Algoritmerne til løsning af problemerne i NP fungerer også i polynomisk tid, men på basis af en fysisk urealiserbar maskinmodel.
Som et alternativ til definitionen via ikke-bestemmelse kan klassen NP også beskrives via verifikation af problemer. Ud over det faktiske input modtager en verifikationsalgoritme også et vidne (også kaldet et certifikat). I et ja-tilfælde skal verifikationsalgoritmen komme til et positivt svar mindst fra et muligt vidne. I tilfælde af en nej-forekomst må verifikationsalgoritmen ikke komme til et positivt svar for noget vidne. Hvis der er en verifikationsalgoritme for et problem, der fungerer med et vidne om polynomlængde i polynomisk tid, ligger dette problem i klassen NP. Et eksempel på et effektivt verificerbart problem er tilfredshedsproblemet (SAT) . Her stilles spørgsmålet, om der er en tildeling af dens variabler til en boolsk formel, så formlen er sand. En mulig verifikationsalgoritme bruger en vektor som et vidne, der koder variabelallokeringen. For en given variabel tildeling er det let at designe en effektiv algoritme, der evaluerer formlen for denne opgave. Så dette problem er i klasse NP. Det er ikke verifikationsalgoritmens opgave at finde belægningen.
En ikke-bestemmende Turing-maskine kan løse et problem i NP ved først at generere alle mulige løsninger, hvorved beregningsstien er forgrenet til et tilsvarende antal stier og derefter verificere hver af disse løsninger, hvilket kan gøres deterministisk, dvs. uden yderligere forgrening.
Der er problemer i NP, der praktisk talt ikke kan løses i store tilfælde. Disse inkluderer NP-komplette problemer. Problemer fra næsten alle områder inden for datalogi kan findes i denne klasse. Men ikke alle problemer i NP er vanskelige, fordi NP også indeholder klasse P.
Sagen P = NP
Hvis P-NP-problemet blev løst i betydningen P = NP, ville vi vide, at selv for NP-komplette problemer skal der være algoritmer, der arbejder med polynomisk tidsforbrug.
Omvendt, da definitionen af NP-fuldstændighed forudsætter algoritmer, hvormed det er muligt at reducere et hvilket som helst antal problemer fra NP i polynomial tid til NP-komplette problemer, med den polynomiske opløsbarhed af endda et enkelt NP-komplet problem, alle klasse NP ville være umiddelbart løselig i polynomisk tid. Dette ville resultere i en problemløsningskraft i hele datalogi, der ikke kan opnås selv med de største fremskridt inden for hardwareudvikling.
På den anden side er en løsning af P-NP-problemet i betydningen P = NP ret uønsket til visse applikationer. For eksempel ville asymmetriske krypteringsmetoder miste en masse sikkerhed, da de derefter kunne opdeles i polynomisk tid.
Sagen P ≠ NP
Hvis P-NP-problemet blev løst i betydningen P P NP, ville det være klart, at yderligere bestræbelser på at finde polynomiske løsninger til NP-komplette problemer ville være meningsløse. Man kan let forestille sig, at bestræbelserne på at finde en effektiv løsning på grund af den store betydning af problemerne i NP kun stoppes, når det har vist sig at være umuligt. Indtil da vil der stadig blive brugt en masse privat og offentlig forskningsenergi.
I mange sætninger i dag antages det imidlertid, at P ≠ NP holder, fordi kun på denne måde kan effektivt forskningsarbejde udføres uden bevis for lighed. Man leder efter veje ud gennem tilnærmelser og heuristikker, efter problemrestriktioner, der ikke forsømmer praksis.
Konsekvenser for kompleksitetsteorien
Et af de vigtigste forskningsmål for kompleksitetsteorien er afgrænsningen af, hvad der er praktisk muligt, og dermed aktiviteten inden for datalogi i sig selv. De foregående afsnit har tydeligtgjort betydningen af denne afgrænsning. I løbet af forsøgene på at løse P-NP-problemet bragte kompleksitetsteorien adskillige resultater frem og gradvis forfinerede dens analysemetoder. Disse resultater bruges i design og analyse af praktisk vigtige algoritmer og har således også en direkte effekt på praktisk datalogi .
Bestræbelserne på at løse P-NP-problemet, som har varet i mere end tredive år, giver den praktiske computerforsker en høj grad af sikkerhed for, at isolerede bestræbelser på effektivt at løse problemer fra NP er mere eller mindre meningsløse. Praktisk datalogi koncentrerer sig derfor om tilnærmede løsninger eller modifikation af de originale problemer, når man løser problemer fra NP. F.eks. Kan problemkompleksiteten af optimeringsalgoritmer reduceres enormt, hvis man ikke stræber efter en optimal løsning, men er tilfreds med en næsten optimal løsning. Kompleksitetsteorien giver den teoretiske opbakning til denne tilgang.
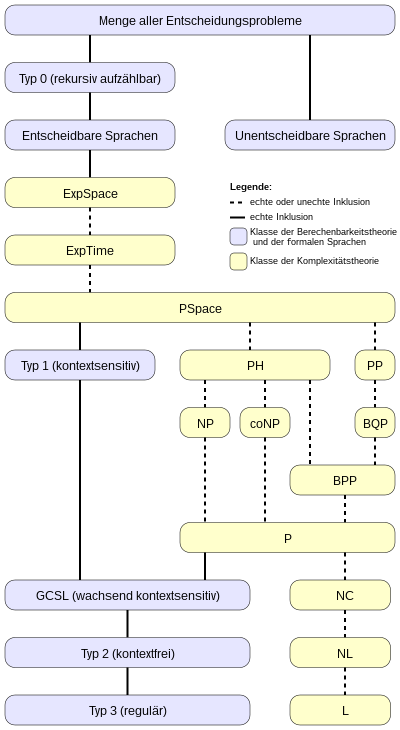
Sprog og kompleksitetskurser
Det følgende inklusionsdiagram giver et - ret groft - overblik over forholdet mellem klasserne for beregningsteori , Chomsky-hierarkiet og de vigtigste kompleksitetsklasser .
Historie af kompleksitetsteori
Efter adskillige grundlæggende termer og vigtige resultater af kompleksitetsteori er blevet forklaret i de foregående afsnit, gives en historisk oversigt i de følgende afsnit, som skal hjælpe med at klassificere den kronologiske rækkefølge af disse resultater.
Grundlæggende
Før den faktiske begyndelse af forskningen eksplicit relateret til algoritmernes kompleksitet blev der udviklet adskillige grundlæggende. Opførelsen af Turing-maskinen af Alan Turing i 1936 kan ses som den vigtigste ; det viste sig at være en ekstremt fleksibel model til senere algoritmeanalyser.
Resultaterne af John Myhill (1960), Raymond Smullyan (1961) og Hisao Yamada (1962), der beskæftigede sig med specielle rum- og tidsbegrænsede problemklasser, men i deres arbejde endnu ikke er begyndt at udvikle en generel teori, betragtes som den første uformelle kompleksitetsteoretiske undersøgelse udviklede sig.
Begyndelsen på kompleksitetsteoretisk forskning
Juris Hartmanis og Richard E. Stearns tager et første store skridt mod en sådan teori i deres arbejde fra 1965 om algoritmernes beregningskompleksitet. De giver allerede en kvantitativ definition af tid og rumskompleksitet og vælger således de to ressourcer, der stadig betragtes som de vigtigste i dag. Dermed vælger de multibånds-Turing-maskinen som basis og træffer således en meget robust beslutning, der er gyldig inden for mange områder af kompleksitetsteori. Du arbejder også allerede på de første hierarkiposter.
En række grundlæggende resultater fremkom i de følgende år. I 1967 offentliggjorde Manuel Blum den Speedup teorem . 1969 fulgte Unionens sætning af Edward M. McCreight og Albert R. Meyer. Og i 1972 offentliggjorde Allan Borodin gap-sætningen. Disse resultater kan ikke kun ses som grundlæggende for kompleksitetsteorien, de repræsenterer også en stikprøve af det stadig nye forskningsområde, som samtidig skal retfærdiggøres med de mest “spektakulære” resultater. Så disse sætninger møder f.eks. Nogle af udsagnene er overraskende, men de er undertiden baseret på antagelser, der ville være begrænset i dag. For eksempel kræves der ingen reelle kompleksitetsfunktioner (se ovenfor).
I samme tidsperiode, der inkluderer omkring de første ti år med kompleksitetsteoretisk forskning, er klasse P formuleret som klassen af "praktisk løselige" problemer. Alan Cobham viser, at polynomtiden er robust under valget af maskinmodellen (som i dag er opsummeret under den udvidede Church-Turing-afhandling). Derudover viser mange matematiske funktioner sig at kunne beregnes på polynomisk tid.
Udforskning af klassen NP
Klassen NP vises først med Jack Edmonds, som oprindeligt kun giver en uformel definition. Det faktum, at mange vigtige problemer ser ud til at ligge i NP'er, gør imidlertid denne klasse til et attraktivt forskningsfelt. Begrebet reducerbarhed og NP-fuldstændighed baseret på det er udviklet og udtrykkes først kortfattet i Cooks (1971) sætning : Problemet med tilfredshed (SAT) er NP-komplet og dermed et af de sværeste problemer i NP. I øvrigt henviste Stephen Cooks originale arbejde til tautologier ( propositionsformler , der er opfyldt ved hver opgave), mens begrebet tilfredshed ikke nævnes. Da resultaterne med hensyn til tautologierne relativt let kan overføres til tilfredshed, tilskrives de imidlertid Stephen Cook. Richard Karp (1972) giver en del af denne overførsel ved at udarbejde reduktionsteknikken. Helt uafhængigt af dette arbejde udviklede Leonid Levin (1973) en teori om NP-fuldstændighed i det daværende Sovjetunion , som i lang tid blev ignoreret i Vesten.
I 1979 udgav Michael R. Garey og David S. Johnson en bog, der beskriver 300 NP-komplette problemer ( Computers and intractability ). Denne bog blev en vigtig reference for fremtidige forskere.
Randomiserede kompleksitetsklasser
1982 repræsenterer Andrew Yao , begrebet trapdoor-funktioner (trapdoor-funktioner), før en særlig type envejsfunktioner repræsenterer (envejsfunktioner), og viser deres grundlæggende betydning i kryptografien . For vanskeligheden ved at knække en kode er den værst tænkelige tilgang til kompleksitetsklasser som NP imidlertid ikke tilstrækkelig. Der må snarere ikke være algoritmer, der løser disse problemer effektivt i en betydelig del af alle tilfælde. Dette svarer til modellen for den sandsynlige Turing-maskine og motiverer introduktionen af randomiserede kompleksitetsklasser såsom ZPP , RP eller BPP (alt introduceret af John T. Gill, 1977).
Med denne oversigt blev de væsentlige hjørnesten i historien om kompleksitetsteori lagt. Som i andre forskningsområder er de nyere resultater opdelt i mange, undertiden meget specielle, underområder.
litteratur
- Sanjeev Arora & Boaz Barak: Computational Complexity. En moderne tilgang . Cambridge University Press, Cambridge 2009, ISBN 978-0-521-42426-4 .
- Ding-Zhu Du & Ker-I Ko: Theory of Computational Complexity. John Wiley & Sons, New York 2000, ISBN 0-471-34506-7 .
- Lance Fortnow & Steve Homer: A Short History of Computational Complexity. 14. november 2002 ( PDF, 225 kB )
- Michael R. Garey & David S. Johnson : Computers and Intractability: A guide to the theory of NP-completeeness. Freeman, New York 2003, ISBN 0-7167-1045-5 .
- Juris Hartmanis & Richard E. Stearns : Om algoritmernes beregningskompleksitet. I: Transaktioner fra American Mathematical Society. Bind 117, 1965, s. 285–306 ( PDF; 2018 KB )
- Jan van Leeuwen (red.): Håndbog om teoretisk datalogi, bind A: algoritmer og kompleksitet. MIT Press / Elsevier, Amsterdam 1994, ISBN 0-262-72020-5 .
- Christos Papadimitriou : Computational Complexity. Addison-Wesley, læsning / messe. 1995, ISBN 0-201-53082-1 .
- K. Rüdiger Reischuk: Complexity Theory - Volume I: Basics: Machine models , time and space complexity, nondeterminism. 2. udgave. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-12275-8 .
- Michael Sipser : Introduktion til teorien om beregning. 2. udgave. Thomson, Boston 2006, ISBN 0-534-95097-3 . (International udgave)
- Ingo Wegener : Kompleksitetsteori. Grænser for algoritmernes effektivitet. 1. udgave. Springer, Berlin 2003, ISBN 3-540-00161-1 .
Weblinks
- Complexity Zoo - Register over de vigtigste kompleksitetsklasser
Fodnoter
- ↑ Sådanne problemer eksisterer f.eks. Inden for probabilistiske kompleksitetsklasser. Hvis man her begrænser fejlsandsynligheden - som det er nødvendigt for praktisk anvendelige sandsynlighedsalgoritmer - er et af resultaterne, at kompleksitetsklasser ikke længere kan tælles. Dette er dog en forudsætning for alle separationsprocesser. Som et resultat kan polynomiske tidsalgoritmer pludselig erstattes af lineære tidsalgoritmer. Eksemplet viser, hvor følsomt netværket af krav og de afledte sætninger generelt er.