Hypergeometrisk fordeling

Sandsynlighed funktion af den hypergeometriske fordeling for .RED: ; blå: ; Grøn: .${\ displaystyle n = 20}$${\ displaystyle M = 20, N = 60}$${\ displaystyle M = 20, N = 30}$${\ displaystyle M = 50, N = 60}$

Den hypergeometriske fordeling er en sandsynlighedsfordeling i stokastik . Det er univariat og er en af ​​de diskrete sandsynlighedsfordelinger . I modsætning til den generelle hypergeometriske fordeling kaldes det også den klassiske hypergeometriske fordeling .

Elementerne er tilfældigt taget fra en todelt population i en prøve uden erstatning . Den hypergeometriske fordeling giver derefter information om sandsynligheden for, at et bestemt antal elementer vil forekomme i prøven, der har den ønskede egenskab. Denne distribution er derfor vigtig for f.eks . Kvalitetskontrol . ${\ displaystyle n}$

Den hypergeometriske fordeling er modelleret på urnemodellen uden udskiftning (se også kombination uden gentagelse ). En urne med to slags bolde betragtes specifikt i denne sammenhæng. Bolde er fjernet uden at erstatte. Den tilfældige variabel er antallet af bolde af den første slags i denne prøve. ${\ displaystyle n}$ ${\ displaystyle X}$

Den hypergeometriske fordeling beskriver således sandsynligheden for, at for givne elementer ("population af omkredsen "), som har den ønskede egenskab, nøjagtigt hits opnås, når der vælges prøver ("prøve af omkredsen ") . H. sandsynligheden for succes i eksperimenter. ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle X = k}$${\ displaystyle n}$

Eksempel 1: Der er 30 bolde i en urne, hvoraf 20 er blå, så 10 er ikke blå. Hvad er sandsynligheden p for at trække nøjagtigt tretten blå kugler fra en prøve på tyve kugler (uden at erstatte)? Svar: p = 0,3096. Dette svarer til den blå bjælke ved k = 13 i diagrammet "Sandsynlighedsfunktion for den hypergeometriske fordeling for n = 20".

Eksempel 2: Der er 45 kugler i en urne, hvoraf 20 er gule. Hvad er sandsynligheden p for at trække nøjagtigt fire gule kugler fra en prøve på ti kugler? Svar: p = 0,269. Eksemplet beregnes nedenfor .

definition

Den hypergeometriske fordeling afhænger af tre parametre:

• antallet af elementer i en befolkning .${\ displaystyle N}$
• antallet af elementer med en bestemt egenskab i dette basissæt (antallet af mulige succeser).${\ displaystyle M \ leq N}$
• antallet af elementer i en prøve.${\ displaystyle n \ leq N}$

Distributionen giver nu oplysninger om, hvor sandsynligt det er, at elementer med egenskaben, der skal kontrolleres (succeser eller hits), er i prøven. Det resultat rum er derfor . ${\ displaystyle k}$ ${\ displaystyle \ Omega}$${\ displaystyle \ {\ max \ {0, n + MN \}, \ dotsc, \ min \ {n, M \} \}}$

En diskret stokastisk variabel er underlagt den hypergeometriske fordeling med parametrene , og , hvis de er sandsynlighederne${\ displaystyle X}$${\ displaystyle M}$${\ displaystyle N}$${\ displaystyle n}$

${\ displaystyle h (k | N; M; n): = P (X = k) = {\ frac {\ displaystyle {M \ vælg k} {NM \ vælg nk}} {\ displaystyle {N \ vælg n} }}}$

for ejer. Den binomialkoefficienten betegner " i ". Så skriver du eller . ${\ displaystyle k \ in \ Omega}$${\ displaystyle {\ tbinom {N} {n}}}$${\ displaystyle N}$${\ displaystyle n}$${\ displaystyle X \ sim Hyp_ {N, M, n}}$${\ displaystyle X \ sim H (N, M, n)}$

Den fordelingsfunktionen angiver derefter sandsynligheden for, at på de fleste elementer med egenskaben skal afprøves i prøven. Denne kumulative sandsynlighed er summen${\ displaystyle H (k \ mid N; M; n)}$ ${\ displaystyle k}$

${\ displaystyle H (k | N; M; n): = P \ left (X \ leq k \ right) = \ sum _ {y = 0} ^ {k} h \ left (y \ mid N; M; n \ right) = \ sum _ {y = 0} ^ {k} {\ frac {\ displaystyle {M \ vælg y} {\ displaystyle {NM} \ vælg {ny}}} {\ displaystyle {N \ vælg n }}}}$.

Alternativ parameterisering

Lejlighedsvis kaldes det også en sandsynlighedsfunktion

${\ displaystyle Hyp_ {B_ {1}, B_ {2}, n} (\ {k \}): = {\ frac {\ displaystyle {B_ {2} \ vælg k} {B_ {1} \ vælg nk} } {\ displaystyle {B_ {1} + B_ {2} \ vælg n}}}}$

Brugt. Dette følger med og ind i ovenstående variant. ${\ displaystyle N = B_ {1} + B_ {2}}$${\ displaystyle M = B_ {2}}$

Egenskaber for den hypergeometriske fordeling

Symmetrier

Følgende symmetrier gælder:

• Byt kugler trukket og succeser: ${\ displaystyle h (k | N; M; n) = h (k | N; n; M)}$
• Byt succeser og fiaskoer: ${\ displaystyle h (k | N; M; n) = h (nk | N; NM; n)}$

Forventet værdi

Den forventede værdi af den hypergeometrisk fordelte tilfældige variabel er ${\ displaystyle X}$

${\ displaystyle \ operatorname {E} (X) = \ sum _ {k = 0} ^ {n} k {\ frac {\ displaystyle {M \ vælg k} {\ displaystyle {NM} \ vælg {nk}}} {\ displaystyle {N \ vælg n}}} = n {\ frac {M} {N}}}$.

mode

Den tilstand af hypergeometriske fordeling er

${\ displaystyle \ left \ lfloor {\ frac {(n + 1) (M + 1)} {N + 2}} \ right \ rfloor}$.

Her er den Gaussiske beslag . ${\ displaystyle \ lfloor \ cdot \ rfloor}$

Variation

Den varians den hypergeometrisk stokastisk variabel er ${\ displaystyle X}$

${\ displaystyle \ operatorname {Var} (X) = \ sum _ {k = 0} ^ {n} k ^ {2} {\ frac {\ displaystyle {M \ vælg k} {\ displaystyle {NM} \ vælg { nk}}} {\ displaystyle {N \ vælg n}}} - \ venstre (n {\ frac {M} {N}} \ højre) ^ {2} = n \, {\ frac {M} {N} } \ left (1 - {\ frac {M} {N}} \ right) {\ frac {Nn} {N-1}}}$,

Den sidste brøkdel er den såkaldte korrektionsfaktor ( finitetskorrektion ) i modellen uden udskiftning.

Skævhed

Den skævheden af den hypergeometriske fordeling er

${\ displaystyle \ operatorname {v} (X) = {\ frac {(N-2M) (N-1) ^ {\ frac {1} {2}} (N-2n)} {[nM (NM) ( Nn)] ^ {\ frac {1} {2}} (N-2)}}}$.

Karakteristisk funktion

Den karakteristiske funktion har følgende form:

${\ displaystyle \ phi _ {X} (t) = {{{NM \ vælg n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; e ^ {it}) } \ over {N \ vælg n}}}$

Hvorved betegner den Gaussiske hypergeometriske funktion . ${\ displaystyle _ {2} F_ {1} (\ cdot; \ cdot; \ cdot)}$

Momentgenererende funktion

Det øjeblik frembringende funktion kan også udtrykkes ved hjælp af hypergeometric funktion:

${\ displaystyle M_ {X} (t) = {\ frac {{NM \ vælg n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; e ^ {t}) } {N \ vælg n}}}$

Sandsynlighedsgenererende funktion

Den sandsynlighedsgenererende funktion er angivet som

${\ displaystyle m_ {X} (t) = {\ frac {{NM \ vælg n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; t)} {N \ vælg n}}}$

Forholdet til andre distributioner

Forholdet til binomialfordelingen

I modsætning til binomialfordelingen med den hypergeometriske fordeling returneres prøverne ikke til reservoiret for yderligere udvælgelse. Hvis størrelsen på prøven er relativt lille (nogenlunde ) sammenlignet med størrelsen af befolkningen , adskiller sandsynlighederne beregnet ved binomialfordelingen og den hypergeometriske fordeling sig ikke væsentligt fra hinanden. I disse tilfælde udføres tilnærmelsen ofte ved hjælp af binomialfordelingen, som er matematisk lettere at håndtere. ${\ displaystyle n}$${\ displaystyle N}$${\ displaystyle n / N <0 {,} 05}$

Forholdet til Pólya-distributionen

Den hypergeometriske fordeling er et specielt tilfælde af Pólya-fordelingen (vælg ). ${\ displaystyle c = -1}$

Forholdet til urnemodellen

Den hypergeometriske fordeling stammer fra den diskrete ensartede fordeling gennem urnemodellen . Fra en urne med i alt kugler farves og kugler trækkes. Den hypergeometriske fordeling indikerer sandsynligheden for, at farvede kugler tegnes. Ellers kan binomialfordelingen også bruges til modellering i praksis. Se også eksemplet. ${\ displaystyle N}$${\ displaystyle M}$${\ displaystyle n}$${\ displaystyle \ max \ {0, n + MN \} \ leq k \ leq \ min \ {n, M \}}$${\ displaystyle k}$

Forholdet til den multivariate hypergeometriske fordeling

Den multivariate hypergeometriske fordeling er en generalisering af den hypergeometriske fordeling. Det besvarer spørgsmålet om antallet af kugler i en farve trukket fra en urne, hvis urnen indeholder mere end to skelnelige farver af kugler. For to farver stemmer det overens med den hypergeometriske fordeling.

Eksempler

Forskellige eksempler

Der er 45 kugler i en container, hvoraf 20 er gule. 10 bolde fjernes uden udskiftning.

Den hypergeometriske fordeling angiver sandsynligheden for, at nøjagtigt x = 0, 1, 2, 3, ..., 10 af de fjernede kugler er gule.

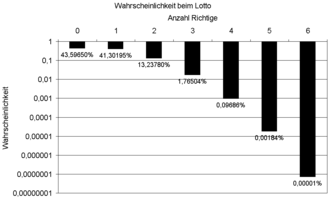
Et eksempel på den praktiske anvendelse af hypergeometrisk distribution er lotteriet : I nummerlotteriet er der 49 nummererede bolde; 6 af disse tegnes i lodtrækningen; 6 numre krydses på lotteriet.

${\ displaystyle h (x | 49; 6; 6)}$angiver sandsynligheden for at opnå nøjagtigt x = 0, 1, 2, 3, ..., 6 "hits".

• Sandsynlighed i det tyske lotteri
• 

  i lineær anvendelse

• 

  i logaritmisk anvendelse

Detaljeret beregningseksempel for kuglerne

For eksemplet med de farvede bolde, der er givet ovenfor, er sandsynligheden at bestemme, at der nøjagtigt 4 gule bolde resulterer.

Samlet antal bolde	${\ displaystyle N = 45}$
Nummer med egenskaben "gul"	${\ displaystyle M = 20}$
Prøvestørrelse	${\ displaystyle n = 10}$
Målrettet mod gul	${\ displaystyle x = 4}$

Så . ${\ displaystyle h (4 | 45,20,10)}$

Sandsynligheden skyldes:

Antal muligheder for at vælge nøjagtigt 4 gule (og derfor nøjagtigt 6 lilla) bolde

divideret med

Antal måder at vælge nøjagtigt 10 bolde i enhver farve

Der er

${\ displaystyle {M \ vælg x} = {20 \ vælg 4} = 4 \, 845}$

Måder at vælge nøjagtigt 4 gule bolde.

Der er

${\ displaystyle {{NM} \ vælg {nx}} = {25 \ vælg 6} = 177 \, 100}$

Måder at vælge nøjagtigt 6 lilla bolde.

Da hver “gul mulighed” kan kombineres med enhver “lilla mulighed”, resulterer dette

${\ displaystyle {M \ vælg x} \ gange {{NM} \ vælg {nx}} = 4 \ .845 \ gange 177 \, 100 = 858 \, 049 \, 500}$

Muligheder for nøjagtigt 4 gule og 6 lilla kugler.

Der er helt

${\ displaystyle {N \ vælg n} = {45 \ vælg 10} = 3 \, 190 \, 187 \, 286}$

Måder at trække 10 bolde på.

Så vi får sandsynligheden

${\ displaystyle P (X = 4) = h (4 | 45; 20; 10) = {\ frac {{20 \ vælg 4} {25 \ vælg 6}} {45 \ vælg 10}} = {\ frac { 4 \, 845 \ cdot 177 \, 100} {3 \, 190 \, 187 \, 286}} \ ca. 0 {,} 2690}$,

i ca. 27 procent af tilfældene fjernes nøjagtigt 4 gule (og 6 lilla) kugler.

Alternativt kan resultatet også findes ved hjælp af følgende ligning

${\ displaystyle P (X = 4) = h (4 | 45; 10; 20) = {\ frac {{10 \ vælg 4} {35 \ vælg 16}} {45 \ vælg 20}} \ ca. 0 {, } 2690}$

Der er 4 gule kugler i prøven . De resterende gule kugler (16) er i de 35 resterende kugler, der ikke er en del af prøven. ${\ displaystyle n = 10}$

Numeriske værdier for eksemplerne

Weblinks

• Lommeregner til enkle og kumulative sandsynligheder for den hypergeometriske fordeling

Individuelle beviser

1. ↑ Hans-Otto Georgii: Stokastik . Introduktion til sandsynlighedsteori og statistik. 4. udgave. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , pp. 36 , doi : 10.1515 / 9783110215274 .