Binomial koefficient

Den binomialkoefficienten er en matematisk funktion , der kan anvendes til at løse en af de grundlæggende problemer i kombinatorik . Det indikerer på hvor mange forskellige måder man kan vælge bestemte objekter fra et sæt forskellige objekter (uden at udskifte uden at være opmærksom på rækkefølgen). Binomialkoefficienten er antallet af -elementundersæt af et -element-sæt. ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$

"49 over 6" i Tyskland eller "45 over 6" i Østrig og Schweiz er z. B. antallet af mulige lodtrækninger i lotteriet (uden at tage det ekstra antal i betragtning).

En binomial koefficient afhænger af to naturlige tal og . Han vil blive markeret med symbolet ${\ displaystyle n}$${\ displaystyle k}$

${\ displaystyle {\ binom {n} {k}}}$

skrevet og talt som “n over k”, “k ud af n” eller “n dyb k”. Den engelske forkortelse nCr for n vælg r findes på lommeregnere.

Disse numre blev navngivet, fordi de fremstår som koefficienter i binomialets kræfter ; den såkaldte binomiale sætning gælder : ${\ displaystyle x + y}$

${\ displaystyle {\ begin {align} (x + y) ^ {n} & = {\ binom {n} {0}} x ^ {n} + {\ binom {n} {1}} x ^ {n -1} y + \ dotsb + {\ binom {n} {n-1}} xy ^ {n-1} + {\ binom {n} {n}} y ^ {n} \\ & = \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} x ^ {nk} y ^ {k} \ end {justeret}}}$

En udvidelse af binomialkoefficienten afledt af kombinatorik er den generelle binomialkoefficient , som bruges i analysen .

definition

For et komplekst tal og et ikke-negativt heltal defineres binomialkoefficienten "n over k" som følger: ${\ displaystyle n}$ ${\ displaystyle k}$

${\ displaystyle {\ begin {align} {\ binom {n} {k}} & = {\ frac {n} {1}} \ cdot {\ frac {n-1} {2}} \ dotsm {\ frac {n- (k-1)} {k}} \\ & = {\ frac {n \ cdot (n-1) \ dotsm (nk + 1)} {k!}} \\ & = \ prod _ { j = 1} ^ {k} {\ frac {n + 1-j} {j}}, \ end {justeret}}}$

hvor betegner den faktuelle af . Det tomme produkt ( ) er inkluderet . ${\ displaystyle k!}$${\ displaystyle k}$${\ displaystyle k = 0}$${\ displaystyle 1}$

Hvis det er et ikke- negativt heltal med , kan definitionen kendt fra kombinatorik anvendes: ${\ displaystyle n}$${\ displaystyle n \ geq k}$

${\ displaystyle {\ binom {n} {k}} = {\ frac {n!} {k! \ cdot (nk)!}}}$

ejendomme

Hvis begrænsningen også foretages til ikke-negative heltal, gælder følgende: ${\ displaystyle k}$${\ displaystyle n}$

• ${\ displaystyle {\ tbinom {n} {k}}}$er altid et ikke-negativt heltal. Er det , så er det ellers .${\ displaystyle k \ leq n}$${\ displaystyle {\ tbinom {n} {k}} \ geq 1}$${\ displaystyle {\ tbinom {n} {k}} = 0}$
• ${\ displaystyle {\ binom {n} {0}} = 1 = {\ binom {n} {n}}}$
• ${\ displaystyle {\ binom {n} {1}} = n = {\ binom {n} {n-1}}$
• ${\ displaystyle {\ binom {n} {k}} = {\ frac {n-k + 1} {k}} {\ binom {n} {k-1}}}$
• ${\ displaystyle {\ binom {n} {k}} = {\ frac {n} {k}} \ cdot {\ binom {n-1} {k-1}} \ Leftrightarrow k \ cdot {\ binom {n } {k}} = n \ cdot {\ binom {n-1} {k-1}}}$
• ${\ displaystyle {\ binom {n + 1} {k + 1}} = {\ binom {n} {k}} + {\ binom {n} {k + 1}}}$. For er den rigtige summand .${\ displaystyle n = k}$${\ displaystyle {\ tbinom {n} {n + 1}} = 0}$

I det generelle tilfælde af reelle eller komplekse værdier for kan nogle af de udtryk, der er givet her, blive udefinerede i den forstand, der er givet ovenfor, hvis de ikke længere skulle være hele og ikke-negative dette vedrører udsagnene , og . Det viser sig dog, at disse udsagn bliver korrekt, hvis, i overensstemmelse med den analytiske generalisering nedenfor, det er beta-funktion også tilladt for komplekse værdier. ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle 1 = {\ tbinom {n} {n}}}$${\ displaystyle n = {\ tbinom {n} {n-1}}}$${\ displaystyle {\ tbinom {n} {n + 1}} = 0}$${\ displaystyle k}$

Symmetri af de binomiale koefficienter

Binomiale heltalskoefficienter er symmetriske i betydningen

${\ displaystyle {\ binom {n} {k}} = {\ binom {n} {nk}}}$

for alle ikke-negative og . ${\ displaystyle n}$${\ displaystyle k}$

bevis

${\ displaystyle {\ begin {align} {\ binom {n} {nk}} & = {\ frac {n!} {(nk)! \ cdot (n- (nk))!}} \\ & = { \ frac {n!} {(nk)! \ cdot k!}} \\ & = {\ frac {n!} {k! \ cdot (nk)!}} \\ & = {\ binom {n} { k}} \ end {justeret}}}$

eksempel

${\ displaystyle {\ binom {5} {3}} = {\ binom {5} {5-3}} = {\ binom {5} {2}}}$

${\ displaystyle {\ binom {5} {3}} = {\ frac {5!} {3! \ cdot (5-3)!}} = {\ frac {5!} {3! \ cdot 2!} } = {\ frac {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5} {(1 \ cdot 2 \ cdot 3) \ cdot (1 \ cdot 2)}} = {\ frac {4 \ cdot 5} {1 \ cdot 2}} = 10}$

${\ displaystyle {\ binom {5} {2}} = {\ frac {5!} {2! \ cdot (5-2)!}} = {\ frac {5!} {2! \ cdot 3!} } = {\ frac {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5} {(1 \ cdot 2) \ cdot (1 \ cdot 2 \ cdot 3)}} = {\ frac {4 \ cdot 5} {1 \ cdot 2}} = 10}$

Rekursiv repræsentation og Pascals trekant

For heltal og med kan binomiale koefficienter også bestemmes ved hjælp af følgende rekursionsregel : ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle 0 \ leq k \ leq n}$${\ displaystyle \ textstyle {\ binom {n} {k}}}$

${\ displaystyle {\ binom {n} {0}} = 1 = {\ binom {n} {n}}}$ for alle ${\ displaystyle n \ geq 0}$

${\ displaystyle {\ binom {n + 1} {k + 1}} = {\ binom {n} {k}} + {\ binom {n} {k + 1}}}$for alle og for alle med${\ displaystyle n> 0}$${\ displaystyle k}$${\ displaystyle 0 \ leq k <n}$

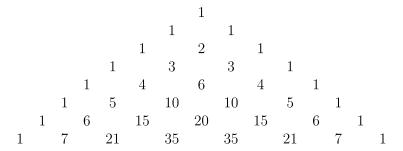
Med deres hjælp er det let at bestemme alle binomiale koefficienter op til en given grænse for , en ordning for dette er Pascal-trekanten : Den rekursive del der svarer til det faktum, at hvert tal er summen af ​​de to tal over det. ${\ displaystyle n}$

Bevis:

${\ displaystyle {\ begin {align} {\ binom {n} {k}} + {\ binom {n} {k + 1}} & = {\ frac {n!} {k! \ cdot (nk)! }} + {\ frac {n!} {(k + 1)! \ cdot (n- (k + 1))!}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n!} {(k + 1) \ cdot k! \ cdot (nk)!}} + {\ frac {n! \ cdot (nk)} {(k + 1)! \ cdot (nk-1)! \ cdot (nk)}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n!} {(k + 1)! \ cdot (nk)!}} + {\ frac {n! \ cdot (nk)} {(k + 1)! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n! + n! \ cdot (nk) )} {(k + 1)! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {n! \ cdot ((k + 1) + (nk))} {(k + 1 )! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {n! \ cdot (n + 1)} {(k + 1)! \ cdot (nk)!}} \\ [ . 5em] & = {\ frac {(n + 1)!} {(K + 1)! \ Cdot ((n + 1) - (k + 1))!}} \\ [. 5em] & = { \ binomial {n + 1} {k + 1}} \ end {justeret}}}$

Koefficienten kan findes i -th linje i -th position (begge tæller fra nul!): ${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$

Den samme trekant repræsenteret i symbolerne: ${\ displaystyle {\ tbinom {n} {k}}}$

Algoritme til effektiv beregning

Der er en effektiv algoritme for heltal , som er produktformlen ${\ displaystyle n}$

${\ displaystyle {n \ vælg k} = \ prod _ {i = 1} ^ {k} {\ frac {n + 1-i} {i}}}$

af binomialkoefficienten. På grund af den konstante ændring mellem multiplikation og division vokser de mellemliggende resultater ikke unødigt. Derudover er alle mellemresultater også naturlige tal.

For at undgå unødvendig beregningsindsats beregnes binomialkoefficienten i tilfælde : ${\ displaystyle k> n / 2}$

${\ displaystyle {n \ vælg nk} = {n \ vælg k}}$

Følgende pseudokode præciserer beregningen:

binomialkoeffizient(n, k)
1  wenn 2*k > n dann k = n-k
2  ergebnis = 1
3  für i = 1 bis k
4      ergebnis = ergebnis * (n + 1 - i) / i
5  rückgabe ergebnis

Regnemaskiner bruger også denne beregningsmetode, hvis de tilbyder funktionen. Ellers ville computerkapaciteten være opbrugt. Mærkningen af ​​funktionstasten med nCr beskriver rækkefølgen af ​​inputværdierne i infixnotation ; først antallet af elementer n, derefter funktionstasten Kombinationer, derefter antallet af valgte objekter r ( betegnet med k i artiklen ). ${\ displaystyle n = 69}$

Beregningen nPr ( permutationer ) tager hensyn til de permutationer af de r elementer, division med er udeladt: ${\ displaystyle r!}$

${\ displaystyle P (n, r) = {\ frac {n!} {(nr)!}}}$.

Den binomiale koefficient i kombinatorik

I kombinatorisk optælling er der

${\ displaystyle {\ binom {n} {k}} = {\ frac {n!} {k! \ cdot (nk)!}}}$

antallet af kombinationer uden gentagelse af elementer af elementer. På grund af denne egenskab spiller binomialkoefficienten en central rolle i kombinatorik og bruges i beregningen og i formlerne til andre kombinatoriske størrelser. ${\ displaystyle k}$${\ displaystyle n}$

Illustration med mængder

Sammenlign også: Kombination (kombinatorik) → Indstil repræsentation

En anden fortolkning af kombinationer uden gentagelse af k ud af n-elementer er antallet af alle- element-undergrupper af et- element-sæt. ${\ displaystyle k}$${\ displaystyle n}$

Det kan fortolkes som følger:

version 1

Først tæller man alle - tupler med parvise forskellige elementer, der kan sættes sammen fra -elementets indledende sæt. Der er muligheder for at vælge det første tupelelement. Efter ethvert valg af dette første er der kun muligheder for det andet element, efter dets valg kun for det tredje osv., Op til muligheder for det th og sidste tuple-element. Antallet af alle tupler sammensat på denne måde er derfor et produkt af faktorer, som ved hjælp af fakultetet også kan noteres som . Nu er imidlertid nøjagtigt hver af de tællede -Tupler permutationer af hinanden og svarer derfor til en og samme -Element-undergruppe. Efter at have divideret med denne "tælemultiplikitet" er resultatet faktisk det ønskede antal undersæt. ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n-1}$${\ displaystyle n-2}$${\ displaystyle n-k + 1}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle n \ cdot (n-1) \ cdot (n-2) \ dotsm (n-k + 2) \ cdot (n-k + 1)}$${\ displaystyle k}$${\ displaystyle {\ tfrac {n!} {(nk)!}}}$${\ displaystyle k!}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle {\ tfrac {n!} {k! \ cdot (nk)!}} = {\ tbinom {n} {k}}}$

Variant 2

En anden, mere symmetrisk illustration understreger ikke handlingen med at vælge fra elementer, men snarere aspektet ved at nedbryde det i to undergrupper af og elementer. Antag, at en -element output tuple består af røde og hvide elementer, der på en eller anden måde er opstillet. Hvis man danner alle permutationer af denne sekvens, kan de hver ikke skelnes med hensyn til farve, fordi permutationer af de røde elementer med hinanden ikke ændrer noget i farvesekvensen, lige så lidt som nogensinde uafhængige permutationer inden for de hvide. Så der er kun farvekodede sekvenser af længden med alle mulige forskellige opgaver, hver med røde elementer. Imidlertid kan hver sekvens nu tildeles entydigt til en af -elementundersæt af et -element-sæt. Det samme gælder på grund af symmetrien af ​​rød og hvid eller af og også for de supplerende delelementer. Det samlede antal af disse undergrupper er således hver . ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle l: = nk}$${\ displaystyle n = l + k}$${\ displaystyle k}$${\ displaystyle l}$${\ displaystyle (k + l)!}$${\ displaystyle k! \ cdot l!}$${\ displaystyle k!}$${\ displaystyle l!}$${\ displaystyle {\ tfrac {(k + l)!} {k! \ cdot l!}} = {\ tbinom {k + l} {k}} = {\ tbinom {k + l} {l}}}$${\ displaystyle k + l}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k + l}$${\ displaystyle k}$${\ displaystyle l}$ ${\ displaystyle l}$${\ displaystyle {\ tbinom {k + l} {k}} = {\ tbinom {n} {k}} = {\ tbinom {n} {nk}} = {\ tbinom {k + l} {l}} }$

eksempel

Følgende gælder for antallet af mulige lodtrækninger eller billetter til den tyske Lotto 6 ud af 49 (uden yderligere nummer eller supernummer):

${\ displaystyle {\ tbinom {49} {6}} = 13.983.816 \ ca. 14 \ {\ tekst {millioner}}}$

Der er naturligvis nøjagtigt en måde at vælge 6 korrekte tal på. tæller mulighederne for 0 korrekte, nemlig at vælge alle 6 tip fra de 43 forkerte. Antallet af forskellige tip med 5 korrekte tal er meget simpelt , fordi der kun er 6 måder at vælge 5 ud af de 6 numre, der er tegnet (eller at udelade et af dem), og så er der i hvert tilfælde måder at placere det udeladte tip på et af de 43 forkerte tal. Generelt er antallet af forskellige tip med korrekte ved 6 resultater fra 49 med samme overvejelse . Ved 6, 0 og 5 rigtige næppe mærke til, at de faktorer der anvendes , og faktisk nemt binomialkoefficienter. Summen af ​​alle de nævnte tipnumre resulterer i det samlede antal 13983816 af alle mulige tip - dette følger af Vandermonde-identiteten nedenfor . ${\ displaystyle {\ tbinom {43} {6}}}$${\ displaystyle 6 \ cdot 43 = 258}$${\ displaystyle 43 = 49-6}$${\ displaystyle r}$${\ displaystyle {\ tbinom {6} {r}} \ cdot {\ tbinom {43} {6-r}}}$${\ displaystyle 1 = {\ tbinom {6} {6}} = {\ tbinom {6} {0}} = {\ tbinom {43} {0}}}$${\ displaystyle 6 = {\ tbinom {6} {5}}}$${\ displaystyle 43 = {\ tbinom {43} {1}}}$

Så sandsynligheden for 6 korrekte tal med et tip er den for 5 korrekte tal . For 0 korrekte tal er resultatet omkring 44%. Den generelle sandsynlighed for at være korrekt er et specielt tilfælde af den hypergeometriske fordeling , der kombinerer tre binomiale koefficienter på denne måde. ${\ displaystyle 1/13983816}$${\ displaystyle 258/13983816}$${\ displaystyle 6096454/13983816}$${\ displaystyle {\ tbinom {6} {r}} \ cdot {\ tbinom {43} {6-r}} / {\ tbinom {49} {6}}}$${\ displaystyle r}$

For flere eksempler, se: Kombination (kombinatorik) → Eksempler

Kombinatorisk bevis

Den kombinatoriske fortolkning tillader også enkle beviser for forholdet mellem binomiale koefficienter, for eksempel ved dobbelttælling . Eksempel: Følgende gælder for: ${\ displaystyle 1 \ leq k \ leq n}$

${\ displaystyle {n \ vælg k} = {n-1 \ vælg k-1} + {n-1 \ vælg k}}$

Bevis: Lad det være et elementært sæt og et fast element. Derefter deles -elementets undergrupper i to klasser: ${\ displaystyle X}$${\ displaystyle n}$${\ displaystyle x \ i X}$${\ displaystyle k}$${\ displaystyle X}$

• de undergrupper, der indeholder de består af sammen med en -elementundersæt af -element-sæt ,${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle (k-1)}$${\ displaystyle (n-1)}$${\ displaystyle X \ setminus \ {x \}}$
• de undergrupper, der ikke indeholder de er -elementundersæt af -elementsættet .${\ displaystyle x}$${\ displaystyle k}$${\ displaystyle (n-1)}$${\ displaystyle X \ setminus \ {x \}}$

Kombinationsmængder

Sættet med underelementer til alle elementer i et sæt betegnes undertiden også på grund af dets magt . Så for hvert begrænset sæt : ${\ displaystyle k}$${\ displaystyle M}$${\ displaystyle {\ tbinom {\ left | M \ right |} {k}}}$${\ displaystyle {\ tbinom {M} {k}}}$${\ displaystyle M}$

${\ displaystyle \ left | {M \ vælg k} \ right | = {\ left | M \ right | \ vælg k}}$

Udtryk med binomiale koefficienter

Summer med binomiale koefficienter

${\ displaystyle \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} = {\ binom {n} {0}} + {\ binom {n} {1}} + \ dotsb + {\ binom {n} {n}} = 2 ^ {n}}$

Denne formel er baseret på en kombinatorisk kendsgerning. Da det samlede antal -elementundersæt af er -elementbeløb, angives antallet ved sammenlægning af alle dets delmængder, altså . Formlen kan også afledes fra binomial sætning ved at sætte. ${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle 2 ^ {n}}$${\ displaystyle x = y = 1}$

Summer med alternerende binomiale koefficienter

${\ displaystyle \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} = {\ binom {n} {0}} - {\ binom {n } {1}} + {\ binom {n} {2}} \ mp \ dotsb + (- 1) ^ {n} {\ binom {n} {n}} = 0}$til .${\ displaystyle n> 0}$

For mærkeligt følger denne formel af symmetrien af ​​den binomiale koefficient. For enhver kan det afledes af binomial sætning ved at indstille og (eller og ). ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle x = 1}$${\ displaystyle y = -1}$${\ displaystyle x = -1}$${\ displaystyle y = 1}$

Summer af binomiale koefficienter med lige eller ulige antal valgte objekter

Ved subtraktion eller tilføjelse til ovenstående ligninger og efterfulgt af halvering for get: ${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} = 2 ^ {n}}$${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} = 0}$${\ displaystyle n> 0}$

${\ displaystyle \ sum _ {k = 0} ^ {[{\ frac {n} {2}}]} {\ binom {n} {2k}} = 2 ^ {n-1}}$som også ; ${\ displaystyle \ sum _ {k = 0} ^ {[{\ frac {n-1} {2}}]} {\ binom {n} {2k + 1}} = 2 ^ {n-1}}$

hvor [] er gaussiske parenteser .

Summen af ​​forskudte binomiale koefficienter

Startende fra induktionsstart for alt, der bruger rekursionsreglen til binomiale koefficienter, er det let at bevise med induktion ved at bruge rekursionsreglen igen: ${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {m = 1} {\ binom {n + k} {n}} = {\ binom {n} {n}} + {\ binom {n + 1 } {n}} = {\ binom {n + 1} {n + 1}} + {\ binom {n + 1} {n}} = {\ binom {n + 1 + 1} {n + 1}} }$${\ displaystyle n}$${\ displaystyle m}$

${\ displaystyle \ sum _ {k = 0} ^ {m} {\ binom {n + k} {n}} = {\ binom {n} {n}} + {\ binom {n + 1} {n} } + \ dotsb + {\ binom {n + m} {n}} = {\ binom {n + m + 1} {n + 1}}}$;

på grund af summands symmetri såvel som summen gælder følgende også:

${\ displaystyle \ sum _ {k = 0} ^ {m} {\ binom {n + k} {k}} = {\ binom {n} {0}} + {\ binom {n + 1} {1} } + \ dotsb + {\ binom {n + m} {m}} = {\ binom {n + m + 1} {m}} = {\ binom {n + m + 1} {n + 1}}}$.

Vandermonde identitet

${\ displaystyle \ sum _ {j = 0} ^ {k} {\ binom {m} {j}} {\ binom {n} {kj}} = {\ binom {m + n} {k}}.}$

Der er også et kombinatorisk argument her: Højre side svarer til antallet af -elementundersæt af et -element-sæt af kugler. Man kan nu forestille sig, at kuglerne har to forskellige farver: kugler er røde og kugler grønne. En -elementær delmængde består derefter af et bestemt antal røde kugler og mange grønne kugler . For hver mulig indikerer den tilsvarende summand til venstre antallet af muligheder for en sådan opdeling i røde og grønne kugler. Summen giver det samlede antal. Et bevis, der ofte opfattes som simpelt, bruger binomial sætning i form ${\ displaystyle k}$${\ displaystyle (m + n)}$${\ displaystyle m}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle j}$${\ displaystyle kj}$${\ displaystyle j}$

${\ displaystyle (1 + x) ^ {n} = \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} x ^ {k},}$

såvel som tilgangen

${\ displaystyle (1 + x) ^ {m} (1 + x) ^ {n} = (1 + x) ^ {m + n}}$

og koefficient sammenligning.

I et specielt tilfælde resulterer Vandermondes identitet i følgende formel for kvadratsummen: ${\ displaystyle k = m = n}$

${\ displaystyle \ sum _ {j = 0} ^ {n} {\ binom {n} {j}} ^ {2} = {\ binom {2n} {n}}}$

Divisionsrester

Er et primtal, og er det så ${\ displaystyle p}$${\ displaystyle n_ {0}, k_ {0} \ in \ {0, \ dotsc, p-1 \}}$${\ displaystyle n_ {1}, k_ {1} \ in \ mathbb {N}}$

${\ displaystyle {\ binom {n_ {0} + pn_ {1}} {k_ {0} + pk_ {1}}} \ equiv {\ binom {n_ {0}} {k_ {0}}} {\ binom {n_ {1}} {k_ {1}}} {\ pmod {p}}.}$

Det betyder, at modulo kan beregnes effektivt ved hjælp af repræsentationerne fra og til basen , nemlig "ciffer for ciffer". ${\ displaystyle p}$${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle p}$

Binomiale koefficienter i analyse

generalisering

En generalisering, der spiller en rolle i beregningen, opnås, hvis man tillader et vilkårligt komplekst tal , men fortsætter med at antage, at det er et heltal. I dette tilfælde er det ${\ displaystyle n}$ ${\ displaystyle \ alpha}$${\ displaystyle k}$

${\ displaystyle {\ binom {\ alpha} {k}} = {\ begin {cases} {\ frac {\ alpha (\ alpha -1) (\ alpha -2) \ dotsm (\ alpha - (k-1) )} {k!}}, & {\ text {if}} \ quad k> 0 \\ 1, & {\ text {if}} \ quad k = 0 \\ 0, & {\ text {if}} \ quad k <0 \ end {cases}}}$

binomialkoefficienten " over " (i det tilfælde er det tomme produkt defineret som 1). Denne definition stemmer overens med ikke-negativt heltal med den kombinatoriske definition (dvs. definitionen af som antallet af alle- elementundersæt af et fast- elementært sæt) og for ikke-negativ med den algebraiske definition (dvs. definitionen af som produktet ). ${\ displaystyle \ alpha}$${\ displaystyle k}$${\ displaystyle k = 0}$${\ displaystyle \ alpha}$${\ displaystyle {\ tbinom {\ alpha} {k}}}$${\ displaystyle k}$${\ displaystyle \ alpha}$${\ displaystyle k}$${\ displaystyle {\ tbinom {\ alpha} {k}}}$${\ displaystyle {\ tfrac {\ alpha} {1}} \ cdot {\ tfrac {\ alpha -1} {2}} \ dotsm {\ tfrac {\ alpha - (k-1)} {k}}}$

For eksempel er

${\ displaystyle {2 {,} 5 \ vælg 2} = {\ frac {2 {,} 5 \ cdot 1 {,} 5} {2!}} = {\ frac {3 {,} 75} {2} } = 1 {,} 875}$

og

${\ displaystyle {-1 \ vælg k} = {\ frac {(-1) (- 2) \ dotsm (-k)} {k!}} = (- 1) ^ {k}.}$

Den anden parameter kan også generaliseres til enhver kompleks opgave, hvis beta-funktionen bruges til at definere: ${\ displaystyle k}$${\ displaystyle z}$ ${\ displaystyle \ mathrm {B} (x, y)}$${\ displaystyle \ alpha \ in \ mathbb {C} \ setminus \ {- 1, -2, -3, \ dotsc \}}$

${\ displaystyle {\ binom {\ alpha} {z}} = {\ frac {1} {(\ alpha +1) \, \ mathrm {B} (z + 1, \ alpha -z + 1)}} = {\ frac {\ Gamma (\ alpha +1)} {\ Gamma (z + 1) \, \ Gamma (\ alpha -z + 1)},}$

hvor betegner den gammafunktionen . Hvis der er eller et negativt heltal, er værdien på højre side 0, fordi de ikke-positive heltal er (kun) polerne i . ${\ displaystyle \ Gamma (z)}$${\ displaystyle z}$${\ displaystyle \ alpha -z}$${\ displaystyle \ Gamma (z)}$

Det er klart, at symmetriforholdet stadig gælder

${\ displaystyle {\ binom {\ alpha} {z}} = {\ binom {\ alpha} {\ alpha -z}}}$,

især

${\ displaystyle {\ binom {\ alpha} {1}} = {\ binom {\ alpha} {\ alpha -1}} = \ alpha}$,

${\ displaystyle {\ binom {\ alpha} {0}} = {\ binom {\ alpha} {\ alpha}} = 1}$

og med en ikke-negativ helhed ${\ displaystyle m}$

${\ displaystyle {\ binom {\ alpha} {- m}} = {\ binom {\ alpha} {\ alpha + m}} = 0}$.

For at udtrække tegnet fra den første parameter, forudsat at det er et heltal, er forholdet

${\ displaystyle {\ binom {- \ alpha} {k}} = (- 1) ^ {k} {\ binom {\ alpha + k-1} {k}}}$

angive.

Generelt for kompleks , forholdet ${\ displaystyle \ alpha}$${\ displaystyle z}$

${\ displaystyle {\ binom {- \ alpha} {z}} = \ left (\ cos (\ pi z) + \ sin (\ pi z) \ cot (\ pi \ alpha) \ right) {\ binom {\ alpha + z-1} {z}}}$.

De multinomiale koefficienter , der kræves, når binomialet generaliseres til det multinomiale sætning , giver en yderligere generalisering .

Binomial-serien

For og med dig opretholde forholdet ${\ displaystyle n \ in \ mathbb {N} _ {0}}$${\ displaystyle z \ in \ mathbb {C} \ setminus \ {1 \}}$${\ displaystyle | z | \ geq 1}$

${\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ binom {k} {n}} {\ frac {1} {z ^ {k + 1}}} = \ sum _ {k = n } ^ {\ infty} {\ binom {k} {n}} {\ frac {1} {z ^ {k + 1}}} = {\ frac {1} {(z-1) ^ {n + 1 }}},}$

som er en generalisering af den geometriske serie og tilhører binomial serien .

Hvis , såvel som , den følgende serie konvergerer i henhold til ${\ displaystyle | z | \ leq 1}$${\ displaystyle z \ neq -1}$${\ displaystyle \ alpha \ in \ mathbb {C}}$

${\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ binom {\ alpha} {k}} z ^ {k} = (1 + z) ^ {\ alpha}.}$

Mere nøjagtige betingelser for og er givet i artiklen Binomial Series . ${\ displaystyle z}$${\ displaystyle \ alpha}$

Sum udtryk for beta-funktionen

Et andet forhold kan bevises for alle relativt let med komplet induktion, ${\ displaystyle m, n \ geq 0}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {m + k + 1}} = { \ dfrac {1} {(m + n + 1) \ displaystyle {\ binom {m + n} {m}}}},}$

hvorfra straks symmetrien

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {m + k + 1}} = \ sum \ limits _ {k = 0} ^ {m} {\ binom {m} {k}} {\ frac {(-1) ^ {k}} {n + k + 1}}}$

følger. En generalisering til med og læser ${\ displaystyle z, s \ in \ mathbb {C}}$${\ displaystyle -z, -s \ notin \ mathbb {N}}$${\ displaystyle s + z \ neq -1}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {\ infty} {\ binom {s} {k}} {\ frac {(-1) ^ {k}} {z + k + 1}} = {\ dfrac {1} {(z + s + 1) \ displaystyle {\ binom {z + s} {s}}}} = \ mathrm {B} (z + 1, s + 1).}$

Gaussisk produktrepræsentation for gamma-funktionen

Den sidste formel fra det foregående afsnit er til ${\ displaystyle -z \ notin \ {0,1,2, \ dotsc, n \}}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {z + k}} = {\ frac {n!} {z \, (z + 1) \, (z + 2) \ dotsm (z + n)}}.}$

Ser man på sagen , udskift brøkene i summen med integraler i henhold til ${\ displaystyle \ operatorname {Re} z> 0}$

${\ displaystyle {\ frac {1} {z + k}} = \ int \ grænser _ {0} ^ {1} t ^ {z + k-1} \ mathrm {d} t}$

og opsummerer summen af ​​kræfterne i henhold til de binomiale formler, man opnår

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {z + k}} = \ int \ grænser _ {0} ^ {1} t ^ {z-1} (1-t) ^ {n} \ mathrm {d} t = n ^ {- z} \ int \ limits _ {0} ^ {n} t ^ {z-1} \ left (1 - {\ frac {t} {n}} \ right) ^ {n} \ mathrm {d} t,}$

hvor substitutionen blev brugt til den sidste integral . Når alt kommer til alt har du ligningen ${\ displaystyle t \ to t / n}$

${\ displaystyle \ int \ limits _ {0} ^ {n} t ^ {z-1} \ left (1 - {\ frac {t} {n}} \ right) ^ {n} \ mathrm {d} t = {\ frac {n ^ {z} \, n!} {z \, (z + 1) \, (z + 2) \ dotsm (z + n)}},}$

hvorfra den gaussiske produktrepræsentation af gammafunktionen skyldes direkte grænseovergangen , ${\ displaystyle n \ to \ infty}$

${\ displaystyle \ Gamma (z) = \ lim \ grænser _ {n \ til \ infty} {\ frac {n ^ {z} \, n!} {z \, (z + 1) \, (z + 2 ) \ dotsm (z + n)}},}$

resultater.

Digamma-funktion og Euler-Mascheroni konstant

For med gælder ${\ displaystyle m, n \ in \ mathbb {N}}$${\ displaystyle m \ leq n}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {m} {\ binom {n} {mk}} {\ frac {(-1) ^ {k-1}} {k}} = {\ binom {n} {m}} \ sum \ limits _ {k = nm + 1} ^ {n} {\ frac {1} {k}},}$

hvilket også kan bevises ved induktion . I det specielle tilfælde er denne ligning forenklet til ${\ displaystyle m}$${\ displaystyle n = m}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ sum \ grænser _ {k = 1} ^ {\ infty} {\ binom {n} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ sum \ grænser _ {k = 1} ^ {n} {\ frac {1} {k}} = H_ {n},}$

hvor er rækkefølgen af ​​de harmoniske tal, dvs. de delvise summer af den harmoniske række . Konverteringen af ​​den venstre total til en serie (grænse i stedet for ) er tilladt på grund af for${\ displaystyle H_ {n}}$${\ displaystyle \ infty}$${\ displaystyle n}$${\ displaystyle {\ tbinom {n} {k}} = 0}$${\ displaystyle n <k.}$

${\ displaystyle H_ {n}}$ er på den anden side repræsentativ som

${\ displaystyle H_ {n} = \ psi (n + 1) - \ psi (1) = \ psi (n + 1) + \ gamma}$

med digamma-funktionen og Euler-Mascheroni-konstanten${\ displaystyle \ psi (n)}$ ${\ displaystyle \ gamma.}$

${\ displaystyle \ psi (n)}$kan fortsættes til komplekse værdier - undtagen negative heltal. Så du får rækken ${\ displaystyle z}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {\ infty} {\ binom {z} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ psi (z + 1) + \ gamma}$

som en kompleks interpolering af rækkefølgen af ​​harmoniske tal.

Trivia

Den bogstavelige oversættelse af " over " til engelsk " over " betegner ikke binomialkoefficienten , men brøkdelen . " Vælg " er korrekt . ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle {\ tfrac {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$

Weblinks

• Download fra BigAl. (Lille, gratis og platformuafhængigt program, blandt andet til den nøjagtige beregning af binomialkoefficienten; med kildekode).
• Online beregning af binomiale koefficienter.

Individuelle beviser

1. ↑ Disquisitiones generelle Cirka seriem infinitam 1 + ... . 1813, s. 26 (også i Carl Friedrich Gauß: Werke. Bind 3, s. 145 ).