Malfatti cirkel

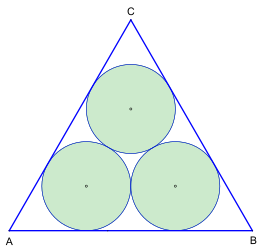
De tre Malfatti-cirkler , senere kendt som Malfatti-problemet , er opkaldt efter Gianfrancesco Malfatti , der erklærede deres konstruktion i 1803. De Malfatti cirkler bestemmes - uanset formen af udgangs trekant - med tre kredse i en trekant med den egenskab, at hver rører de to andre kredse udefra og to sider af trekanten indefra.

Malfatti antog fejlagtigt, at denne egenskab ved cirklerne løste problemet med at pakke tre cirkler i en trekant uden at overlappe hinanden på en sådan måde, at de har det maksimale areal . Hvorfor Malfatti-cirklerne ikke kan løse dette såkaldte Malfatti-maksimeringsproblem , dvs. den maksimale dækning af det trekantede område med tre cirkler , kan f.eks. B. kan let genkendes af en lang, smal højre trekant .

Følgende gælder for radierne af Malfatti-cirklerne i en trekant ABC:

${\ displaystyle r_ {A} = {\ frac {r} {2 (sa)}} (sr - ({\ overline {IB}} + {\ overline {IC}} - {\ overline {IA}})) }$

${\ displaystyle r_ {B} = {\ frac {r} {2 (sb)}} (sr - ({\ overline {IC}} + {\ overline {IA}} - {\ overline {IB}})) }$

${\ displaystyle r_ {C} = {\ frac {r} {2 (sc)}} (sr - ({\ overline {IA}} + {\ overline {IB}} - {\ overline {IC}})) }$

Det står for cirkelradius og halv omkreds af trekanten. er centrum for cirklen og er de tre halveringslinjer . ${\ displaystyle r}$${\ displaystyle s}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}, \ omega _ {\ gamma}}$

Historie

Marmorproblemet
Trekantet prisme med tre indskrevne cylindriske søjler og de ni mulige kontaktpunkter i Malfatti-cirklerne

Det oprindelige Malfatti-problem henviste til et problem fra stereotomi , hvis formodede løsning Malfatti fandt i 1802 og blev offentliggjort i 1803 i Memoria di Matematica e Fisica della Società Italiana delle Scienze i sin artikel Memoria sopra un problema stereotomico . I begyndelsen af ​​sin artikel formulerer Malfatti den aktuelle opgave.

Frit oversat lyder det:

I tilfælde af et ret trekantet prisme lavet af ethvert materiale, f.eks. Marmor, skæres der tre [cirkulære] cylindre derfra med samme højde som prismen, men med det højest mulige samlede volumen, dvs. med mindst mulig materialespild af prismevolumenet.

I sin artikel Memoria sopra un problema stereotomico påpeger Malfatti også, at denne stereotomiske opgave kan reduceres til et problem med overfladegeometri. Han definerer placeringen af ​​de cirkler, der er indskrevet i trekanten, nu kaldet Malfatti-cirkler, som følger:

Gratis oversættelse

Givet en trekant, konstruer tre cirkler i den, så hver af cirklerne er tangent (dvs. de berører et punkt) med de to andre og med tre sider af trekanten.

Dette blev imidlertid afvist i 1992 af WA Salgaller og GA Los, som viste, at løsningen i stedet opnås ved at indskrive en cirkel med det største område i successive trin - beskrevet nedenfor i konstruktionssektionen ifølge Salgaller og Los .

Allerede i 1687 blev Malfatti-konstruktionsproblemet løst af Jakob I Bernoulli i et specielt tilfælde, og senere gav Jakob Steiner og Alfred Clebsch løsninger på en rent geometrisk måde , sidstnævnte med elliptiske funktioner (1857, Crelle's Journal). Den japanske Ajima Naonobu kom også med en løsning 30 år før Malfatti i sammenhæng med japansk arkitektur. At Malfattis konstruktion ikke løste Malfatti-problemet i alle tilfælde blev allerede vist af Lob og Richmond i 1930 ved hjælp af ligesidede trekanter og Howard W. Eves i 1965 med undersøgelser med smalle og lange trekanter. I 1967 blev det endda vist i et essay af Michael Goldberg, at Malfattis konstruktion aldrig gjorde dette. Som nævnt ovenfor fremlagde Salgaller og Los 1992 bevis herfor.

Geometriske konstruktioner

I 2003 forklarede Ingmar Lehmann forskellige løsninger på Malfatti-problemet i sin analyse Malfatti-problemet - et emne i promoveringen af ​​begavede studerende . Fire metoder er beskrevet detaljeret nedenfor.

Malfatti konstruktion

Malfatti cirkler i henhold til Malfatti, beregningsskitse

Variant med tidligere beregninger

Til dette formål udleder Lehmann tre ligninger ved hjælp af Pythagoras sætning og ligheden mellem trekanter , hvis løsninger er tilvejebragt ved de tangente segmenter og . ${\ displaystyle x \; = {\ overline {AC_ {1}}}, \; y = {\ overline {BC_ {2}}}}$${\ displaystyle z = {\ overline {CA_ {2}}}}$

Følgende forhold tages også i betragtning:

${\ displaystyle {\ overline {AI}} = {\ sqrt {r ^ {2} + s ^ {2}}}, \; \; \; {\ overline {BI}} = {\ sqrt {r ^ { 2} + t ^ {2}}}, \; \; \; {\ overline {CI}} = {\ sqrt {r ^ {2} + u ^ {2}}},}$

der betyder udtrykkene

${\ displaystyle s = {\ overline {AL_ {c}}}, \; t = {\ overline {BL_ {c}}}}$ og ${\ displaystyle u = {\ overline {CL_ {a}}}.}$

Med de anvendte passende værdier er det nu muligt at bestemme en såkaldt hjælpesektion${\ displaystyle {\ overline {PQ}}}$ med længden${\ displaystyle m}$

${\ displaystyle m = {\ frac {1} {2}} \ left ({\ overline {AI}} + {\ overline {BI}} + {\ overline {CI}} - {\ overline {AL_ {c} }} - {\ overline {BL_ {c}}} - {\ overline {CL_ {a}}} + r \ right),}$

gælder derefter for de tangentafsnit, der er beskrevet ovenfor

${\ displaystyle x = {\ overline {AC_ {1}}} = {\ overline {AI}} - m, \; \; \; y = {\ overline {BC_ {2}}} = {\ overline {BI }} - m, \; \; \; z = {\ overline {CA_ {2}}} = {\ overline {CI}} - m.}$

Tildeltes individuelt til summerne i formlen for faktoren${\ displaystyle m}$${\ displaystyle {\ frac {1} {2}}}$

${\ displaystyle m = {\ frac {1} {2}} {\ overline {AI}} + {\ frac {1} {2}} {\ overline {BI}} + {\ frac {1} {2} } {\ overline {CI}} - {\ frac {1} {2}} {\ overline {AL_ {c}}} - {\ frac {1} {2}} {\ overline {BL_ {c}}} - {\ frac {1} {2}} {\ overline {CL_ {a}}} + {\ frac {1} {2}} r,}$

en meget enkel og pladsbesparende geometrisk konstruktion (se tilstødende billede) kan vises.

Malfatti cirkler til Malfatti med opførelse af hjælpestrækningen${\ displaystyle {\ overline {PQ}}}$

Konstruktion beskrivelse

Efter at have tegnet en z. B. ulige-sidet trekant med side længder og den centrum af den indskrevne cirkel bestemmes ved anvendelse af de tre halveringslinjer og . Dette resulterer i linjerne og det følger lodlinjen fra til linjen med basispunktet og tegningen af ​​den indskrevne cirkel rundt med radius Lodlinjen fra op til med basispunktet og fra op til basispunktet følger. ${\ displaystyle ABC}$ ${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$ ${\ displaystyle {\ overline {AI}}, {\ overline {BI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle L_ {a}}$${\ displaystyle k}$${\ displaystyle I}$ ${\ displaystyle {\ overline {IL_ {a}}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle L_ {b}}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle L_ {c}}$

Nu bestemmes længden af hjælpestrækningen på en lige linje som følger . Først halveres sporene og tilføjes, fra summen af sporhalvdelene og trækkes til sidst, og den opnåede rest halvdel Inkreisradius tilføjes. ${\ displaystyle m}$${\ displaystyle {\ overline {PQ}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AI}}, \; {\ frac {1} {2}} {\ overline {BI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CI}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {AL_ {c}}}, \; {\ frac {1} {2}} {\ overline {BL_ {c}}}}$${\ displaystyle {\ frac {1} {2}} {\ overline {CL_ {a}}}}$${\ displaystyle {\ frac {1} {2}} r}$

Det næste trin er at bestemme centrumene for Malfatti-cirklerne. Afhente den ekstra afstand med kompasset og overføre den til de tre halveringslinjer og fra midten af cirklen ; dette resulterer i punkterne og fra punkterne og en bue op til siden af ​​trekanten og fra en bue op til og med punkterne og Det følger opstillingen af ​​tre lodrette vinkler fra basispunkterne og på den relevante halvering og dermed de søgte centerpunkter og resultat${\ displaystyle {\ overline {PQ}},}$${\ displaystyle m,}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ displaystyle D, \; E}$${\ displaystyle F.}$${\ displaystyle D}$${\ displaystyle E}$${\ displaystyle c}$${\ displaystyle F}$${\ displaystyle a}$${\ displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}.}$${\ displaystyle C_ {1}, \; C_ {2}}$${\ displaystyle A_ {2}}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma};,}$${\ displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}.}$

For at få kontaktpunkter og tre plumb nejer nødt til at blive fældet fra midtpunkter og på trekanten sider og igen . Endelig trækker i de Malfatti cirkler og med radier og og du får deres sidste tre kontaktpunkter og${\ displaystyle B_ {2}, \; A_ {1}}$${\ displaystyle B_ {1}}$${\ displaystyle M_ {A}, \; M_ {B}}$${\ displaystyle M_ {C}}$${\ displaystyle b, \; a}$${\ displaystyle b}$${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle r_ {A}, \; r_ {B}}$${\ displaystyle r_ {C}}$${\ displaystyle G, \; H}$${\ displaystyle J.}$

Således de tre Malfatti kredse og med deres ni mulige kontaktpunkter og er konstrueret. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; G, \; H }$${\ displaystyle J}$

Konstruktion ifølge Steiner-Petersen

I 1826 bragte Jakob Steiner Malfatti-cirklerne i forbindelse med cirklerne, der består af tre undertriangler, som derfor kan bruges som et konstruktionselement til Malfatti-cirklerne. Steiner formulerede følgende sætning:

Det skal her understreges, at tangenterne til Malfatti-cirklerne nævnt af Steiner generelt ikke er halveringslinjer , men deres spejlbilleder på de lige linjer, der forbinder to cirkelcentre af de delvise trekanter. ${\ displaystyle \ trekant ABC}$

I 1879 fandt Julius Petersen en elementær geometrisk løsning på Malfattis byggeproblem, som er vist nedenfor.

Konstruktion beskrivelse

Af hensyn til klarheden er det fordelagtigt at vise konstruktionen i tre hovedtrin, (1) - (3). Kun de relevante konstruktionselementer overføres fra det første til det andet eller fra det andet til det tredje hovedtrin.

Malfatti-cirkler ifølge Steiner-Petersen
(1) Hovedtrin: Konstruktion af de tre cirkler af de delvise trekanter og${\ displaystyle \ trekant BCI, \; \ trekant CAI}$${\ displaystyle \ trekant ABI}$

(1) Konstruktion af de tre incircles af de delvise trekanter og${\ displaystyle \ trekant BCI, \; \ trekant CAI}$${\ displaystyle \ trekant ABI.}$

Efter at have tegnet en z. B. ulige sidetrekant med sidelængderne og midten af ​​den indskrevne cirkel bestemmes ved hjælp af de tre halveringslinjer og . Inkreismittelpunkte og undertriangler og igen opnået som skæringspunktet mellem to halveringslinjer, z. B. ved at kvartere vinklerne og Det følger faldet af vinkelret på linjen med basispunktet og tegningen af ​​den indskrevne cirkel rundt med radius Fældning af vinkelret fra op til basispunktet og fra op til basispunktet og tegningen af ​​de sidste to Incircles og omkring deres midtpunkter eller er forbundet. ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle M_ {P}, \; M_ {Q}}$${\ displaystyle M_ {R}}$${\ displaystyle \ trekant BCI, \; \ trekant CAI}$${\ displaystyle \ trekant ABI}$${\ displaystyle \ alpha, \; \ beta,}$${\ displaystyle \ gamma.}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle P}$${\ displaystyle k_ {P}}$${\ displaystyle M_ {P}}$${\ displaystyle {\ overline {M_ {P} P}}.}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle Q}$${\ displaystyle M_ {R}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle R}$${\ displaystyle k_ {Q}}$${\ displaystyle k_ {R},}$${\ displaystyle M_ {Q}}$${\ displaystyle M_ {R},}$

Malfatti cirkler ifølge Steiner-Petersen
(2) hovedtrin: konstruktion af de tre tangenter og${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

(2) Konstruktion af de tre tangenter og${\ displaystyle {\ overline {RZ}}, {\ overline {PX}}}$${\ displaystyle {\ overline {QY}}}$

Det fortsætter med forbindelsespunkterne med at skære sporet ind og tegne i Thales-cirklen. Han skærer den indskrevne cirkel i punkterne og tiltrækker dig nu den første tangent fra punktet gennem det punkt, hvor den indskrevne cirkel, indtil de når siden af ​​trekanten i snit. ${\ displaystyle R}$${\ displaystyle M_ {P},}$${\ displaystyle {\ overline {RM_ {P}}}}$${\ displaystyle M_ {1}}$ ${\ displaystyle k_ {1}.}$${\ displaystyle k_ {P}}$${\ displaystyle K}$${\ displaystyle L.}$${\ displaystyle R}$${\ displaystyle L}$${\ displaystyle k_ {P},}$${\ displaystyle b}$${\ displaystyle Z}$

Efter dette, med ruten forbundet i halveret og dalcirklen placeret. Han skærer den indskrevne cirkel i punkterne og tegningen af ​​den anden tangent fra punktet igennem, indtil de når siden af ​​trekanten i snit, lever krydset Da et punkt på den tredje tangent skal være, kræver det kun, at det bestemmes en linje med op til siden af ​​trekanten og skæringspunktet. Således bestemmes også den tredje tangent . ${\ displaystyle P}$${\ displaystyle M_ {Q}}$${\ displaystyle {\ overline {PM_ {Q}}}}$${\ displaystyle M_ {2}}$${\ displaystyle k_ {2}}$${\ displaystyle k_ {Q}}$${\ displaystyle O}$${\ displaystyle N.}$${\ displaystyle P}$${\ displaystyle N,}$${\ displaystyle b}$${\ displaystyle X}$${\ displaystyle T.}$${\ displaystyle T}$${\ displaystyle Q}$${\ displaystyle T}$${\ displaystyle c}$${\ displaystyle Y.}$${\ displaystyle {\ overline {QY}}}$

Malfatti-cirkler ifølge Steiner-Petersen
(3) hovedtrin: konstruktion af Malfatti-cirkler og${\ displaystyle k_ {A}, k_ {B}}$${\ displaystyle k_ {C}}$

(3) Opførelse af Malfatti-cirklerne og${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$

Først tegnes halveringen fra punktet til halveringen i trekanten ; dette resulterer i centrum for den første Malfatti-cirkel. Dette efterfølges af at droppe vinkelret fra linjen med basispunktet og tegne den første Malfatti-cirkel rundt med radius. Fældning af vinkelret fra op til med basispunktet og fra på tangenten til basispunktet følger. Følgende linje ned igennem til symmetrilinien skaber midtpunktet. Efter den anden Malfatti cirkel er tegnet i med radius , perpendikulærerne er skåret fra op med basispunktet fra op med basispunktet og fra på tangenten med basispunktet . Følgende linje ned igennem til vinkelhalvering skaber midtpunktet. Nu den tredje Malfatti cirkel trækkes rundt med radius${\ displaystyle ARZ}$${\ displaystyle \ omega _ {\ epsilon}}$${\ displaystyle R}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {1}}$${\ displaystyle k_ {A}}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} C_ {1}}}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle B_ {2}}$${\ displaystyle M_ {A}}$${\ displaystyle RZ}$${\ displaystyle C '}$${\ displaystyle M_ {A}}$${\ displaystyle C '}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle M_ {B}.}$${\ displaystyle k_ {B}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} C '}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle C_ {2},}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle A_ {1}}$${\ displaystyle M_ {B}}$${\ displaystyle PX}$${\ displaystyle A '}$${\ displaystyle M_ {B}}$${\ displaystyle A '}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle M_ {C}.}$${\ displaystyle k_ {C}}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {M_ {C} A '}}.}$

Til kontaktpunkter og at opnå, kræver det stadig to lodninger udfældet fra centrum på af på og forbindelsen af punktet med${\ displaystyle A_ {2}, \; B_ {1}}$${\ displaystyle B '}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {BC}},}$${\ displaystyle M_ {C}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {C}.}$

Således de tre Malfatti kredse og med deres ni mulige kontaktpunkter og er konstrueret. ${\ displaystyle k_ {A}, \; k_ {B}}$${\ displaystyle k_ {C}}$${\ displaystyle C_ {1}, \; C_ {2}, \; A_ {1}, \; A_ {2}, \; B_ {1}, \; B_ {2}, \; A ', \; B '}$${\ displaystyle C '}$

Konstruktion ifølge Lob og Richmond

Konstruktion ifølge H. Lob og HW Richmond,
ligesidet trekant med indskrevet cirkel som en del af løsningen på maksimeringsproblemet

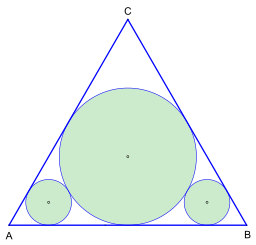
H. Lob og HW Richmond offentliggjorde en løsning på Malfattis maksimeringsproblem i 1930. Den indskrevne cirkel i den ligesidede trekant bruges som en cirkel på tre. Dækningen af ​​det trekantede område ved dette arrangement af cirklerne er kun marginalt større, nemlig ved , men opgaven er let og kan repræsenteres med lille indsats. ${\ displaystyle \ ca. 1 \, \%}$

Du har bevist

Konstruktion beskrivelse

Efter at have tegnet en ligesidet trekant med sider af lige længde og , bestemmes midten af ​​den indskrevne cirkel ved hjælp af de tre halveringslinjer og . Dette efterfølges af faldet af vinkelret på linjen med basispunktet og tegningen af ​​den indskrevne cirkel omkring radius, skæringspunkterne er med halveringslinjen og med halveringspunktet. Fældning af den vinkelrette fra op til basispunktet og fra op til basispunktet følger . ${\ displaystyle ABC}$${\ displaystyle a, \; b}$${\ displaystyle c}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}, \ omega _ {\ beta}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle D}$${\ displaystyle k}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle E}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle F}$${\ displaystyle \ omega _ {\ beta}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle G}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle H}$

For de mindre cirkler du tegne to paralleller til den linje (i en ligesidet trekant)  - en fra det punkt op til den linje med krydset , den anden fra det punkt på linjen med krydset Etableringen af den vinkelrette med bunden på bisector og opsætning af vinkelret på halveringspunktet med basispunktet resulterer i midtpunkterne, og nu tegnes en cirkel rundt med radius og en cirkel rundt med radius . For at få de sidste to kontaktpunkter, felles to lodde bobber på, fra og fra , hvilket resulterer i basispunkterne og${\ displaystyle {\ overline {AB}}}$${\ displaystyle E}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle J}$${\ displaystyle F}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle K.}$${\ displaystyle J}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle K}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}.}$${\ displaystyle M_ {A}}$${\ displaystyle {\ overline {M_ {A} E}}}$${\ displaystyle M_ {B}}$${\ displaystyle {\ overline {M_ {B} F}}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle M_ {A}}$${\ displaystyle M_ {B}}$${\ displaystyle L}$${\ displaystyle M.}$

Således de tre cirkler og med deres ni mulige kontaktpunkter og er konstrueret i den ligesidede trekant . ${\ displaystyle k, \; k_ {A}}$${\ displaystyle k_ {B}}$${\ displaystyle D, \; E, \; F, \; G, \; H, \; J, \; K, \; L}$${\ displaystyle M}$

Goldberg konstruktion

Michael Goldberg offentliggjorde et essay i 1967, hvori han viste, at Malfattis konstruktion, uanset formen på trekanten, på ingen måde kan tilfredsstille maksimeringsproblemet. Han kom til dette resultat - uden at bevise det - gennem undersøgelser med forskellige former for trekanterne, som alle havde en ting til fælles: en af ​​de tre cirkler var altid den indskrevne cirkel.

Konstruktion beskrivelse

Konstruktion ifølge Goldberg, generel trekant med en indskrevet cirkel som en af ​​de tre cirkler, der løser maksimeringsproblemet.
Radius herfra følger: Den tredje cirkel ligger på halvdelen${\ displaystyle {\ overline {SR}} <{\ overline {OM}},}$${\ displaystyle \ omega _ {\ alpha}.}$

Efter tegning af den uregelmæssige trekant bestemmes midten af den indskrevne cirkel ved hjælp af de to halveringslinjer og . Dette resulterer i strækning og efterfølges af udfældning af loddemetal af afstanden til foden punkt og trækningen af den indskrevne cirkel til radius af skæringspunktet på er tilfældet, lodningen af den med basispunktet samt på til foden punkt omfatter se . ${\ displaystyle ABC}$${\ displaystyle I}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle \ omega _ {\ gamma}}$${\ displaystyle {\ overline {AI}}}$${\ displaystyle {\ overline {CI}}.}$${\ displaystyle I}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle D}$${\ displaystyle I}$${\ displaystyle {\ overline {ID}};}$${\ displaystyle \ omega _ {\ alpha}}$${\ displaystyle E.}$${\ displaystyle I}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle F}$${\ displaystyle I}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle G}$

Midten af ​​den anden cirkel bestemmes nu meget let i to trin. Der er behov for kun et vinkelret på fra punktet den i stykker, og en bisector af vinklen Pointen således fremstillede er centrum for den anden cirkel med radius og kontaktpunkterne og med to sider af trekanten. ${\ displaystyle {\ overline {AI}}}$${\ displaystyle E,}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle H}$${\ displaystyle AHE.}$${\ displaystyle J}$${\ displaystyle {\ overline {JE}}}$${\ displaystyle K}$${\ displaystyle L}$

For at finde den størst mulige radius for den tredje og sidst søgte cirkel bestemmes mulige radier først på to halveringer - på tre, hvis trekantsformen kræver det. Det opnås ved analog gentagelse af konstruktionstrinnene i den anden cirkel med et midtpunkt. De stiplede linjer i det tilstødende billede viser den radius, der er konstrueret på halveringen som en sammenligning med radien . Evalueringen af ​​de to radier resulterer . Det følger heraf: Cirklen omkring centrum er den største mulige tredje cirkel, der søges. ${\ displaystyle J.}$${\ displaystyle \ omega _ {\ beta}}$${\ displaystyle {\ overline {SR}},}$${\ displaystyle {\ overline {OM}}}$${\ displaystyle \ omega _ {\ alpha}.}$${\ displaystyle {\ overline {SR}} <{\ overline {OM}}}$${\ displaystyle O}$

Konstruktion ifølge Salgaller og Los

WA Salgaller og GA Los offentliggjorde - efter deres bevis i 1992 (se Historie ) - i 1994 i Journal of Mathematical Sciences deres løsning på Malfattis maksimeringsproblem. Dette inkluderer fem generelle trekanter kan ses i hver, hvor den indskrevne cirkel er en af ​​de tre ikke-overlappende cirkler. Kun i en trekant deraf, beskrevet i en konstruktion ifølge Goldberg , ligger disse tre cirkler på den samme halvering.

Gratis oversættelse

Trekanten er dækket af tre cirkler

• Malfatti-metoden (fig. 1) og Steiner-Petersen-metoden blev opnået

${\ displaystyle \ left ({\ sqrt {3}} - {\ frac {3} {2}} \ right) \ cdot \ pi \ approx 0 {,} 72910}$ eller ca. ${\ displaystyle 72 {,} 91 \, \%.}$

• Metoden ifølge Lob og Richmond (fig. 2) opnået

${\ displaystyle {\ frac {11 {\ sqrt {3}}} {81}} \ cdot \ pi \ approx 0 {,} 73895}$ eller ca. ${\ displaystyle 73 {,} 90 \, \%.}$

• Metode med cirkel i henhold til Salgaller og Los samt metoden ifølge Goldberg (billede 3 og billede 4):

Dækningen af ​​det trekantede område, f.eks. B. som en procentværdi af den valgte form af outputtrekanten samt placeringen af ​​cirklerne og afhængig. For de viste figurer med de tilsvarende områder gælder den procentvise formel:${\ displaystyle k_ {2}}$${\ displaystyle k_ {3}}$${\ displaystyle A}$

${\ displaystyle {\ frac {A_ {k_ {1}} + A_ {k_ {2}} + A_ {k_ {3}}} {A {_ {\ trekant {ABC}}}}} \ cdot 100 \, \%,}$

dette resulterer i en dækning af det trekantede areal for trekanten i figur 3 af og for trekanten i figur 4 af${\ displaystyle \ cirka 72 {,} 70 \; \%}$${\ displaystyle \ ca. 77 {,} 1 \; \%.}$

• 

  Figur 1: Metode af Malfatti og metoden ifølge Steiner-Petersen i en ligesidet trekant, der dækker det trekantede område ca. 72,91%

• 

  Figur 2: Metode ifølge Lob og Richmond i den ligesidede trekant, dækning af det trekantede område ca. 73,90%

• 

  Fig. 3: Salgaller- og Los-metoden samt Goldbergs metode med indskrevet cirkel ; i den viste form er dækningen af ​​det trekantede areal ca. 72,70% ${\ displaystyle k_ {1}}$

• 

  Fig. 4: Salgaller- og Los-metoden samt Goldbergs metode med indskrevet cirkel ; i den viste form er dækningen af ​​det trekantede område ca. 77,1% ${\ displaystyle k_ {1}}$

litteratur

• Kurt Loeber: Bidrag til løsningen og historien om Malfattian-problemet og dets udvidelser. Indledende afhandling. SUB Göttingen, Göttingen Digitaliseringscenter, 1914, adgang til den 4. oktober 2020 . 
• Marco Andreatta, Andras Bezdek, Jan P. Boronski: Malfatti-problemet: to århundreders debat , Mathematical Intelligencer, 2011, nr. 1.
• Heinrich Dörrie : Malfattis problem i 100 store problemer med elementær matematik: deres historie og løsninger . Dover, New York 1965, ISBN 0-486-61348-8 , s. 147-151.
• Michael Goldberg: Om det originale Malfatti-problem i matematik. Mag. Nr. 40, 1967, s. 241-247.
• Charles Stanley Ogilvy: Udflugter i geometri . Dover, New York 1990, ISBN 0-486-26530-7 .
• WA Salgaller, GA Los: Løsningen på Malfattis problem . I: Journal of Mathematical Sciences . 72, nr. 4, 1994, s. 3163-3177.

Weblinks

• Eric W. Weisstein : Malfatti Circles . På: MathWorld (engelsk).
• Eric W. Weisstein : Malfattis problem . På: MathWorld (engelsk).
• Malfattis problem. I: Skær knuden. Hentet 4. oktober 2020 . 

Individuelle beviser

1. ↑ Kurt Loeber: Historisk overblik (introduktion). I: Bidrag til løsningen og historien om Malfattian-problemet og dets udvidelser. SUB Göttingen, Götinger Digitaliseringscenter, 1914, s. 1 , adgang til 15. november 2020 . 
2. Spring op ↑ Gianfrancesco Malfatti: Memoria sopra un problema stereotomica , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, s. 235-244, adgang til 15. november 2020.
3. Spring op ↑ Gianfrancesco Malfatti: Memoria sopra un problema stereotomica , Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, s. 243 ff. Adgang til den 15. november 2020.
4. ↑ ^{a b} Ingmar Lehmann: 1. Malfatti-historien, side 1. (PDF) I: Malfatti-problemet - et emne til fremme af talentfulde mennesker. TU Dortmund University, 2003, adgang til den 19. november 2020 . 
5. ↑ ^{a b c d} Ingmar Lehmann: 1. Malfatti-historien, side 2. (PDF) I: Malfatti-problemet - et emne til fremme af talentfulde studerende. TU Dortmund University, 2003, adgang til den 7. november 2020 . 
6. ↑ ^{a b c d} Raúl Ibáñez: El problema de Malfatti. culturacientifica, Matemoción, 5. april 2017, adgang til 5. oktober 2018 (spansk). 
7. ↑ ^{a b c} Sic! - I henhold til transkriptionsreglerne på den tysksprogede Wikipedia (fodnote 6) adskiller denne stavning Los sig fra stavemåden Los ' (med apostrof), som stort set findes andre steder , se z. B. også her.
8. Mar ^{a b c d} Ingmar Lehmann: Konstruktion af Malfatti-cirklerne, s. 3-5. (PDF; 143 KB) I: The Malfatti Problem - A Topic in Promoting the Gifted, 15 sider. TU Dortmund University, 2003, adgang til den 4. oktober 2020 . 
9. ↑ ^{a b} Kurt Loeber: Historisk overblik (introduktion). I: Bidrag til løsningen og historien om Malfattian-problemet og dets udvidelser. SUB Göttingen, Götinger Digitaliseringscenter, 1914, s. 2 ff. , Adgang til 4. oktober 2020 . 
10. ^ Jacques Bernoulli: Oeuvres complètes, Genève 1744, bind 1, s. 303.
11. ↑ Jakob Steiner: Nogle geometriske propositioner ; Jacob Steiner's Gesammelte Werke, bind 1, G. Reimer, 1881, s. 3, i Google-bogsøgning, adgang til den 15. november 2020
12. Ste Jakob Steiner: Nogle geometriske overvejelser ; Jacob Steiners Gesammelte Werke, bind 1, G. Reimer, 1881, s. 19, i Google-bogsøgning, adgang til den 15. november 2020
13. ^ Alfred Clebsch: Anvendelse af de elliptiske funktioner til et problem med rumets geometri. I: Journal for Pure and Applied Mathematics (Crelle's Journal), bind 53. SUB Göttingen, Götinger Digitaliseringscenter, 1857, s. 292–308 , tilgængelig den 15. november 2020 . 
14. ^ Ajima Naonobu i sit hovedværk Fukyo sampo fra 1799. John J. O'Connor, Edmund F. Robertson :  Malfatti-cirkel. I: MacTutor History of Mathematics arkiv .
15. ^ ^{A b} H. Lob, HW Richmond: On the Solutions of Malfattis Problem for a Triangle. (PDF) London Mathematical Society, 1930, adgang til 20. november 2020 . 
16. ^ ^{A b} Michael Goldberg: Om det originale Malfatti-problem . I: Florida Atlantic University (red.): Mathematics Magazine . bånd 40 , nr. 5. november 1967, s. 241-247 , JSTOR : 2688277 ( Om det originale Malfatti-problem [PDF; adgang til 20. november 2020]). 
17. ↑ Ingmar Lehmann: Konstruktion ifølge Steiner-Petersen, side 5. (PDF) I: Malfatti-problemet - et emne i promoveringen af ​​begavede studerende. TU Dortmund University, 2003, adgang den 2. oktober 2018 . 
18. ↑ Julius Petersen, R. von Fischer-Benzon (Überstzer): Metoder og teorier til løsning af geometriske konstruktionsopgaver. I: Konstruktionsaufgabe 404. University of Michigan, Library, 1879, s. 102-104 , adgang til 15. november 2020 . 
19. ↑ ^{a b} Ingmar Lehmann: Konstruktion ifølge Steiner-Petersen, s. 8 ff. (PDF) I: Malfatti-problemet - et emne til fremme af talentfulde studerende. TU Dortmund University, 2003, adgang den 2. oktober 2018 . 
20. ↑ Sic! - Denne betegnelse Salgaller svarer til Wikipedia: navngivningskonventioner , se også Wiktor Abramowitsch Salgaller
21. ^ ^{A b} W. A. ​​Salgaller, GA Los: Løsningen på Malfattis problem . I: Journal of Mathematical Sciences . 72, nr. 4, 1994, s.  3163 ff., Fig. 1, Springer Link, PDF . Hentet 5. oktober 2020.
22. ↑ Jaime Rangel-Mondragon: Malfatti-problemet. (PDF) I: Wolfram Demonstrations Project. Wolfram, 2011, adgang til 24. november 2020 . 
23. ^ Arnold Math Jn: 2.2 Løsning på Malfattis marmorproblem. (PDF) I: On Malfatti's Marble Problem. Institute for Mathematical Sciences, Stony Brook University, New York, juni 2016, adgang til 24. november 2020 . 

Denne artikel blev tilføjet til listen over fremragende artikler i denne version den 25. november 2020 .