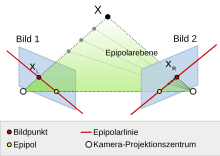
Epipolar geometri

To kameraer optager en scene fra forskellige synsvinkler. Den epipolære geometri beskriver forholdet mellem de to billeder.

Den epipolar geometri (sjældent også nuklear ray geometri ) er en matematisk model fra geometri , der repræsenterer de geometriske relationer mellem forskellige kamera billeder af det samme objekt. Med deres hjælp kan afhængigheden mellem tilsvarende billedpunkter beskrives - dvs. de punkter, som et enkelt objektpunkt genererer i de to kamerabilleder. Selvom dets fundament blev undersøgt af Guido Hauck i 1883 , af Sebastian Finsterwalder i 1899 og af Horst von Sanden i 1908 , blev epipolar geometri kun vigtigere med den automatiske evaluering af digitale billeder, især inden for maskinvision .

Den epipolære geometri bruges primært til at opnå 3D-information fra billeder. Det understøtter korrespondanceanalysen , dvs. tildelingen af ​​tilsvarende punkter, og reducerer den krævede søgeanstrengelse betydeligt.

princip

Illustration med pinhole-kameraet

Et kamera kan modelleres geometrisk ved hjælp af et pinhole-kamera . Med dette ligger hvert punkt på det optagede objekt, projektionscentret og det tilknyttede billedpunkt på en lige linje under optagelsen . Hvis objektpunktet blev optaget to gange fra forskellige positioner, kan skæringspunktet mellem de to lige linjer og dermed koordinaterne for objektpunktet beregnes i en senere evaluering ved hjælp af kameraernes retning. En 3D-rekonstruktion er således mulig, hvis billedpunkterne på et objektpunkt er blevet lokaliseret i begge billeder. Den epipolære geometri tjener til at understøtte denne lokalisering: hvis punktet er angivet i det første billede, hvis den epipolære geometri er kendt, er søgeområdet i det andet billede begrænset til en linje.

Skematisk gengivelse af den epipolære geometri

De geometriske forhold er illustreret i grafikken til venstre. Foruden billed- og objektpunkterne og de to projektionscentre vises de to billedplaner for de to kameraer. Disse foldes foran projektionscentre. Dette gør repræsentationen lettere, men ændrer ikke de geometriske forhold. Objektpunktet X er kortlagt på billedpunktet x _L i kamerabilledet 1 . Fra dette billedpunkt er det kun muligt at bestemme den tilknyttede stråle, som X ligger på. Mulige objektpunkter X ₁ , X ₂ eller X ₃ , der ligesom X svarer til billedpunktet x _L , ligger på denne stråle. Denne stråle og dermed alle mulige objektpunkter afbildes på en lige linje, når objektet optages fra en anden position i det andet billede. Søgningen efter billedpunktet x _R svarende til billedpunktet x _L i det andet billede reduceres til dette .

Ved hjælp af den epipolære geometri kan der etableres et simpelt forhold mellem tilsvarende punkter uden kendskab til kamerapositionerne. Selvom information om kameraernes relative position til hinanden kan stamme fra en kendt epipolær geometri, er det ikke nødvendigt at kende kameraets positioner eksplicit for at bestemme det. Den epipolære geometri afhænger kun af kameraernes parametre og er derfor uafhængig af strukturen på den optagede scene.

Betingelser for epipolar geometri

Der findes fast terminologi til at beskrive epipolar geometri og dens elementer . Flyet, der spænder over kameraets to projektionscentre og det optagede objektpunkt, kaldes det epipolære plan . Dette skærer de to billeder i en lige linje, den såkaldte epipolære linje . Kun på denne kan en tilsvarende pixel til et givet punkt i det andet billede ligge. Den lige linje, der forbinder kameraets to projektionscentre, trænger gennem de to billedplaner på ét punkt hver, epipolen. De to epipoler ændrer ikke deres position i det respektive billede, så længe kameraernes position over for hinanden forbliver stabil. Epipolen i et billede er samtidig billedet af det andet kameras projektionscenter. Alle de epipolære linjer i et billede løber gennem det, men afhængigt af kameraernes placering i forhold til hinanden kan det være uden for det faktiske billede.

Inden for fotogrammetri blev udtrykkene kernestrålegeometri, kernepunkt, kerneplan og kernelinje delvist brugt i stedet for epipolær geometri, epipol, epipolært plan og epipolær linje.

Ansøgninger

Den epipolære geometri bruges hovedsageligt i projektiv geometri , fotogrammetri og computersyn . Dens hovedformål er at støtte korrespondanceanalyse. Hvis det tilsvarende punkt søges i det andet billede for et fremtrædende punkt i det ene billede, skal hele billedet undersøges, hvis den epipolære geometri er ukendt. Hvis den epipolære geometri er kendt, kan søgningen efter det tilsvarende punkt begrænses til den epipolære linje. Dette resulterer i en betydelig reduktion i søgeområdet . Af denne grund anvendes den epipolære geometri hovedsageligt, hvor en scene eller et objekt skal analyseres hurtigt og med lille indsats i tre dimensioner ved hjælp af kameraer. Vigtige anvendelsesområder er computerbaseret vision , måling af emner til kvalitetskontrol, bygningsundersøgelser til arkitektonisk fotogrammetri eller luftfotogrammetri til oprettelse af kort .

Computersyn

Når man søger efter korrespondance til objektidentifikation, begrænser den epipolære geometri søgeområdet til de epipolære linjer og opnår derved en enorm besparelse i computertiden. Samtidig reducerer det antallet af forkerte tildelinger af tilsvarende punkter ved at begrænse søgeområdet. Begge er af stor fordel, fordi de fremskynder algoritmerne og gør dem mere pålidelige (mere robuste). Især inden for autonom robotik kræves enkle beregninger for korte computertider på den ene side på grund af den begrænsede hardware på mobile platforme og på den anden side på grund af behovet for hurtige reaktioner for at undgå kollisioner. For eksempel brugte en deltager i DARPA Grand Challenge , en konkurrence for ubemandede landbiler, OpenCV- programbiblioteket , som indeholder hurtige rutiner til beregning af den epipolære geometri og dens anvendelse i korrespondanceanalyse.

Selvkalibrering af kameraer

3D-rekonstruktion af en scene fra fotografier kræver, at kameraernes interne og relative orientering er kendt. Da den epipolare geometri beskriver det lineære projektive forhold mellem to billeder, bruges den til den såkaldte selvkalibrering, dvs. automatisk bestemmelse af kameraparametrene. Den epipolære geometri bruges til at bestemme den (lineære) indre orientering og den relative orientering ud fra kendte korrespondancer (se afsnit #Beregning ). Enhver eksisterende (ikke-lineær) forvrængning skal være bestemt på forhånd ved hjælp af en kamerakalibrering.

historie

Fig. 1a fra tabel I i Haucks artikel illustrerer citatet.

Historien om epipolar geometri er tæt knyttet til fotogrammetriens historie . Den første til at analysere de underliggende geometriske forhold var matematikeren Guido Hauck. I 1883 offentliggjorde han en artikel i Journal for Pure and Applied Mathematics , hvor udtrykket kernepunkt blev brugt for første gang :

Baseret på Haucks arbejde udviklede Sebastian Finsterwalder en algoritme til en 3D-rekonstruktion fra to ukalibrerede fotos i 1899. Horst von Sanden skrev en første, mere omfattende præsentation i 1908 som en del af sin afhandling Bestemmelsen af ​​nøglepunkterne i fotogrammetri . I dette arbejde beskrev han metoder til en enklere og mere præcis bestemmelse af nøglepunkterne.

I den såkaldte analoge fotogrammetri med optomekanisk fotografering og evaluering, der var frem til indførelsen af ​​digital teknologi, blev korrespondanceanalysen udført manuelt. Da en menneskelig operatør let kan tildele tilsvarende punkter, hvis scenestrukturen er tilstrækkelig, blev resultaterne næppe anvendt. Kun fremkomsten af ​​digital fotogrammetri med digital fotografering og computerstøttet offline evaluering fra 1980'erne og det stigende behov for automatiseret billedevaluering inden for maskinsyn resulterede i en fornyet, mere intensiv undersøgelse af epipolar geometri og dens anvendelse. Et første stykke arbejde, der beviser genopdagelsen af ​​emnet var udgivelsen af Christopher Longuet-Higgins i tidsskriftet Nature . Siden da har mange forskere studeret epipolar geometri, herunder Huang og Faugeras, Horn og Vieville og Lingrand.

Matematisk beskrivelse

Den epipolære geometri skaber et forhold mellem billedkoordinaterne for de tilsvarende punkter. Billedkoordinaterne er ofte angivet i kartesiske koordinater , men kan også gives i affine koordinater . Oprindelsen til et billeds koordinatsystem er normalt i midten eller i et hjørne af billedet. I tilfælde af digitale billeder (CCD-billeder eller scannede billeder) kan f.eks. Rækken og søjlen i pixels bruges som koordinater. Hvis række- og kolonneopløsningerne adskiller sig, eller koordinatsystemets akser ikke er vinkelrette på hinanden, er disse koordinater affine.

Forholdet mellem billedkoordinaterne for tilsvarende punkter er beskrevet af en grundlæggende matrix. Det kan bruges til at bestemme den tilknyttede epipolære linje i det andet billede for et givet punkt i det første billede, hvorpå det tilsvarende punkt er placeret.

Homogene koordinater og projektionsmatrix

Kortlægningen af ​​objektpunkterne på billedplanet kan beskrives med de homogene koordinater, der anvendes i projektiv geometri . Sammenlignet med kartesiske eller affine koordinater udvides homogene koordinater med en koordinat og er kun unikke op til en skaleringsfaktor. De to-dimensionelle kartesiske eller affine koordinater svarer til de homogene koordinater . De homogene koordinater , som ikke alle må være nul på samme tid, og repræsenterer det samme punkt i et todimensionalt projektivt rum , det projicerende plan . Det samme gælder for tredimensionelt rum. ${\ displaystyle (x, \, y)}$${\ displaystyle (u, \, v, \, w) = (wx, \, wy, \, w)}$${\ displaystyle (u, \, v, \, w)}$${\ displaystyle (u / w, \, v / w, \, 1) = (x, \, y, \, 1)}$ ${\ displaystyle \ mathbb {P} ^ {2}}$

Hvert punkt i todimensionelt rum eller tredimensionelt rum kan beskrives ved hjælp af homogene koordinater. Imidlertid svarer et punkt i det affine rum kun til et punkt i det projicerende rum, hvis det er. Punktene i det projicerende plan med kaldes punkter ved uendelig . Da de kan fortolkes som skæringspunkter af parallelle lige linjer, skelnes der ikke mellem parallelle og ikke-parallelle lige linjer i projektiv geometri. Dette er fordelagtigt i perspektiv, for eksempel når man beskriver forsvindingspunkter . Da ligningen svarer til ligningen med en lige linje i det projicerende plan, kaldes sæt af punkter ved uendelig en lige linje ved uendelig . ${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle w \, \ neq \, 0}$${\ displaystyle w \, = \, 0}$${\ displaystyle w \, = \, 0}$

Med homogene koordinater kan kortlæggelsen af ​​de tredimensionelle objektpunkter med koordinaterne på det todimensionale billedplan beskrives som en lineær funktion: ${\ displaystyle (X, \, Y, \, Z)}$

${\ displaystyle \ mathbf {x} = {\ begin {pmatrix} u \\ v \\ w \ end {pmatrix}} = \ mathbf {P} \ mathbf {X} = {\ begin {pmatrix} p_ {11} & p_ {12} & p_ {13} & p_ {14} \\ p_ {21} & p_ {22} & p_ {23} & p_ {24} \\ p_ {31} & p_ {32} & p_ { 33} & p_ {34} \ end {pmatrix}} {\ begin {pmatrix} X \\ Y \\ Z \\ 1 \ end {pmatrix}}.}$

De kartesiske (eller affine) billedkoordinater fås fra og i givet fald . Projektionsmatricen 3 × 4 beskriver perspektivisk kortlægning af objektets punkter på billedplanet. Den indeholder data vedrørende kameraets retning. Da en dimension - objektets afstand fra kameraet - går tabt i denne kortlægning, kan den ikke vendes klart. ${\ displaystyle x = u / w}$${\ displaystyle y = v / w}$${\ displaystyle w \, \ neq \, 0}$ ${\ displaystyle \ mathbf {P}}$

Forholdet mellem tilsvarende punkter

Afledningen af ​​den grundlæggende matrix er baseret på ideen om at vælge et punkt i det første billede , derefter bestemme ethvert objektpunkt, der er kortlagt på dette billedpunkt, og endelig beregne dets billedpunkt i det andet billede. Dette punkt og epipolen er placeret på den tilknyttede epipolære linje i billedplanet for det andet billede og beskriver således tydeligt dem. ${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {X}}$${\ displaystyle \ mathbf {x} _ {2}}$${\ displaystyle \ mathbf {x} _ {2}}$${\ displaystyle \ mathbf {e} _ {2}}$${\ displaystyle \ mathbf {x} _ {1}}$

Hvis der er et punkt i det første billede, kan strålen, hvorpå det tilknyttede objektpunkt ligger, specificeres ved hjælp af den tilknyttede projektionsmatrix . Selve objektpunktet kan ikke bestemmes, fordi afstanden fra kameraet er ukendt. Ethvert punkt på strålen kan beregnes med pseudo-inversen : ${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {P} _ {1}}$ ${\ displaystyle \ mathbf {P} _ {1} ^ {+}}$

${\ displaystyle \ mathbf {X} = \ mathbf {P} _ {1} ^ {+} \ mathbf {x} _ {1}.}$

Dette punkt kan kortlægges i det andet billede med det andet kameras projektionsmatrix : ${\ displaystyle \ mathbf {P} _ {2}}$

${\ displaystyle \ mathbf {x} _ {2} = \ mathbf {P} _ {2} \ mathbf {X} = \ mathbf {P} _ {2} \ mathbf {P} _ {1} ^ {+} \ mathbf {x} _ {1}.}$

Dette betyder, at et punkt på den epipolare linje, som det tilhører, er kendt i det andet billede. Et andet punkt på denne epipolære linje er epipolen , som er billedet af det første kameras projektionscenter : ${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {e} _ {2}}$${\ displaystyle \ mathbf {O} _ {1}}$

${\ displaystyle \ mathbf {e} _ {2} = \ mathbf {P} _ {2} \ mathbf {O} _ {1}.}$

Den epipolar linie er beskrevet i homogene koordinater ved den rette linje ligning , hvorved den cross produkt kan beregnes ud fra de to specificerede rette linje punkter: ${\ displaystyle \ mathbf {l} _ {2} ^ {\ text {T}} \ mathbf {x} _ {2} = 0}$${\ displaystyle \ mathbf {l} _ {2}}$

${\ displaystyle \ mathbf {l} _ {2} = \ mathbf {e} _ {2} \ times \ mathbf {x} _ {2} = (\ mathbf {P} _ {2} \ mathbf {O} _ {1}) \ times (\ mathbf {P} _ {2} \ mathbf {P} _ {1} ^ {+} \ mathbf {x} _ {1}).}$

Dette krydsprodukt kan også skrives som en matrixmultiplikation med en skæv-symmetrisk matrix : ${\ displaystyle \ mathbf {S}}$

${\ displaystyle \ mathbf {l} _ {2} = (\ mathbf {S} _ {\ mathbf {P} _ {2} \ mathbf {O} _ {1}} \ mathbf {P} _ {2} \ mathbf {P} _ {1} ^ {+}) \ mathbf {x} _ {1} = \ mathbf {F} \ mathbf {x} _ {1},}$

hvor udtrykket i parentes kombineres for at danne den grundlæggende matrix. Ligningen af ​​den epipolære linje og forholdet mellem tilsvarende punkter lyder således: ${\ displaystyle \ mathbf {F}}$

${\ displaystyle \ mathbf {l} _ {2} ^ {\ text {T}} \ mathbf {x} _ {2} = \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf { l} _ {2} = \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf {F} \ mathbf {x} _ {1} = 0}$

eller:

${\ displaystyle {\ begin {pmatrix} x_ {2} & y_ {2} & 1 \ end {pmatrix}} {\ begin {pmatrix} f_ {11} & f_ {12} & f_ {13} \\ f_ { 21} & f_ {22} & f_ {23} \\ f_ {31} & f_ {32} & f_ {33} \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\ y_ {1} \\ 1 \ end {pmatrix}} = 0}$.

Denne ligning kaldes den epipolære ligning.

En specialisering af den grundlæggende matrix er den essentielle matrix. Dette resulterer, når der anvendes standardiserede billedkoordinater, hvor oprindelsen til det kartesiske billedkoordinatsystem ligger i billedets hovedpunkt . Da denne betingelse ikke behøver at være opfyldt for den grundlæggende matrix, nøjes den med færre antagelser sammenlignet med den essentielle matrix.

Egenskaber ved den grundlæggende matrix

Den grundlæggende matrix (også kaldet bifokal tensor) indeholder al information om den epipolære geometri. Det kan også bestemmes ud fra billedkoordinaterne for de tilsvarende punkter uden kendskab til kameraernes orientering (det vil sige uden kendskab til projektionsmatricerne og projektionscentret ). ${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {P} _ {1}}$${\ displaystyle \ mathbf {P} _ {2}}$${\ displaystyle \ mathbf {O} _ {1}}$

Den 3 × 3 grundlæggende matrix kan kun bestemmes klart op til en skaleringsfaktor, da multiplikationen af ​​den grundlæggende matrix med et andet tal end 0 ikke ændrer gyldigheden af ​​den epipolære ligning. Dette betyder, at kun 8 af de 9 elementer oprindeligt er uafhængige. Da matrixen - ligesom enhver skæv-symmetrisk matrix med ulige  - er ental , er ental, så determinanten er 0. Denne yderligere betingelse reducerer den grundlæggende matrixs frihedsgrad til 7. ${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf {F} \ mathbf {x} _ {1} = 0}$${\ displaystyle \ mathbf {S} _ {\ mathbf {P} _ {2} \ mathbf {O} _ {1}}}$${\ displaystyle n \ times n}$${\ displaystyle n}$${\ displaystyle \ mathbf {F}}$

Ved hjælp af den grundlæggende matrix kan den tilsvarende epipolære linje beregnes for et punkt i det første billede i det andet billede: ${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {l} _ {2}}$

${\ displaystyle \ mathbf {l} _ {2} = \ mathbf {F} \ mathbf {x} _ {1},}$

og omvendt til et punkt i det andet billede den epipolare linje på det første billede: ${\ displaystyle \ mathbf {x} _ {2}}$${\ displaystyle \ mathbf {l} _ {1}}$

${\ displaystyle \ mathbf {l} _ {1} = \ mathbf {F} ^ {\ text {T}} \ mathbf {x} _ {2}.}$

En given epipolær linje i det ene billede kan ikke bruges til at beregne det oprindelige punkt i det andet billede. For at gøre dette skal den grundlæggende matrix vendes inverteret , hvilket ikke er muligt på grund af dets singularitet.

Da epipolen ligger på alle epipolære linjer , skal den ${\ displaystyle \ mathbf {e} _ {2}}$${\ displaystyle \ mathbf {l} _ {2}}$

${\ displaystyle \ mathbf {l} _ {2} ^ {\ text {T}} \ mathbf {e} _ {2} = (\ mathbf {F} \ mathbf {x} _ {1}) ^ {\ text {T}} \ mathbf {e} _ {2} = \ mathbf {x} _ {1} ^ {\ text {T}} \ mathbf {F} ^ {\ text {T}} \ mathbf {e} _ {2} = 0}$

gælder for alle sådanne, at epipolen og følgelig epipolen fra ligningerne ${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {e} _ {2}}$${\ displaystyle \ mathbf {e} _ {1}}$

${\ displaystyle \ mathbf {F} ^ {\ text {T}} \ mathbf {e} _ {2} = \ mathbf {0} \ qquad {\ text {and}} \ qquad \ mathbf {F} \ mathbf { e} _ {1} = \ mathbf {0}}$

kan bestemmes. Det kan også ses af disse ligninger, at determinanten for den grundlæggende matrix skal være 0, ellers ville ligningerne kun have løsningerne . ${\ displaystyle \ mathbf {e} _ {1} = \ mathbf {e} _ {2} = \ mathbf {0}}$

beregning

Den grundlæggende matrix og dermed den epipolære geometri kan beregnes - som vist i afsnittet Forholdet mellem tilsvarende punkter - med en kendt kalibrering af de to kameraer direkte fra begge projektionsmatricer og et projektionscenter. Da beregningen af ​​den grundlæggende matrix normalt udføres inden projektionsmatricerne bestemmes, forekommer denne sag sjældent. I det følgende forklares det, hvordan det kun kan beregnes ved hjælp af punktkorrespondenser. ${\ displaystyle \ mathbf {F}}$

For at bestemme den grundlæggende matrix ud fra et sæt tilsvarende pixels multipliceres den epipolare ligning: ${\ displaystyle \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf {Fx} _ {1} = 0}$

${\ displaystyle x_ {2} x_ {1} f_ {11} + x_ {2} y_ {1} f_ {12} + x_ {2} f_ {13} + y_ {2} x_ {1} f_ {21} + y_ {2} y_ {1} f_ {22} + y_ {2} f_ {23} + x_ {1} f_ {31} + y_ {1} f_ {32} + f_ {33} = 0}$

eller i vektornotation:

${\ displaystyle {\ begin {pmatrix} x_ {2} x_ {1} & x_ {2} y_ {1} & x_ {2} & y_ {2} x_ {1} & y_ {2} y_ {1} & y_ {2} & x_ {1} & y_ {1} & 1 \ end {pmatrix}} \ cdot \ mathbf {f} = 0}$

Med

${\ displaystyle \ mathbf {f} = {\ begin {pmatrix} f_ {11} & f_ {12} & f_ {13} & f_ {21} & f_ {22} & f_ {23} & f_ {31} & f_ {32} & f_ {33} \ end {pmatrix}} ^ {\ text {T}}.}$

Følgende homogene system med lineære ligninger kan etableres ud fra punktkorrespondenser (det øverste indeks angiver punktnummeret): ${\ displaystyle n}$

${\ displaystyle {\ begin {pmatrix} x_ {2} ^ {1} x_ {1} ^ {1} & x_ {2} ^ {1} y_ {1} ^ {1} & x_ {2} ^ {1 } & y_ {2} ^ {1} x_ {1} ^ {1} & y_ {2} ^ {1} y_ {1} ^ {1} & y_ {2} ^ {1} & x_ {1} ^ {1} & y_ {1} ^ {1} & 1 \\\ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ vdots & \ vdots \\ x_ {2} ^ { n} x_ {1} ^ {n} & x_ {2} ^ {n} y_ {1} ^ {n} & x_ {2} ^ {n} & y_ {2} ^ {n} x_ {1} ^ {n} & y_ {2} ^ {n} y_ {1} ^ {n} & y_ {2} ^ {n} & x_ {1} ^ {n} & y_ {1} ^ {n} & 1 \ ende {pmatrix}} \ cdot \ mathbf {f} = \ mathbf {A} \ cdot \ mathbf {f} = \ mathbf {0}.}$

Da koordinaterne for de tilsvarende punkter opfylder den epipolære ligning, er kolonnerne lineært afhængige af . I det ideelle tilfælde har matrixen derfor højst rang 8. Imidlertid, hvis der er mere end 8 linjer, gælder dette kun, hvis der ikke er nogen måleunøjagtigheder i koordinaterne og ingen forkert tildelte punktpar. Da det ikke har fuld søjlerangering, er der en løsning til (bortset fra den trivielle løsning ) fra nulrummet i . ${\ displaystyle \ mathbf {A}}$ ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {f} = \ mathbf {0}}$${\ displaystyle \ mathbf {A}}$

Ved bestemmelse af korrespondancerne opstår der normalt mindre måle unøjagtigheder, da billedpunkterne kun kan lokaliseres med en begrænset grad af nøjagtighed. Den grundlæggende matrix bestemt ud fra opløsningsvektoren har derfor ikke rang 2 og er derfor ikke ental. Som et resultat skærer de epipolære linjer i et billede, der er bestemt med denne grundlæggende matrix, ikke længere alle i epipolen. ${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {F}}$

I praksis anvendes to metoder til at beregne den grundlæggende matrix, der tager denne singularitetsbetingelse i betragtning: 7-punktsalgoritmen og 8-punktsalgoritmen. I begge metoder bruges de målte koordinater for billedpunkterne normalt ikke direkte, men snarere normaliseres koordinaterne på forhånd. Koordinatsystemerne forskydes i begge billeder på en sådan måde, at oprindelsen ligger i pixelernes tyngdepunkt, og koordinaterne skaleres derefter, så deres værdier er i størrelsesorden 1. Med denne normalisering kan der opnås en betydelig forbedring af resultaterne.

7-punkts algoritme

Denne procedure bruger 7-punkts korrespondancer til at beregne den grundlæggende matrix . Da kun op til en faktor er entydig, er 7 point sammen med betingelsen tilstrækkelige til at bestemme de 9 elementer i . Med 7-punkts korrespondancer indeholder ligningssystemet kun 7 ligninger. Der er derfor to lineært uafhængige løsninger og fra nullrummet af . Den grundlæggende matrix bestemmes som en lineær kombination af matricerne og dannes af og : ${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ det (\ mathbf {F}) = 0}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {A} \ mathbf {f} = \ mathbf {0}}$${\ displaystyle \ mathbf {f} _ {1}}$${\ displaystyle \ mathbf {f} _ {2}}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {f} _ {1}}$${\ displaystyle \ mathbf {f} _ {2}}$${\ displaystyle \ mathbf {F} _ {1}}$${\ displaystyle \ mathbf {F} _ {2}}$

${\ displaystyle \ mathbf {F} = \ alpha \ mathbf {F} _ {1} + (1- \ alpha) \ mathbf {F} _ {2} \ quad {\ text {with}} \ quad \ alpha \ i \ mathbb {R}.}$

For at vælge en af de løsninger, der har rang 2, bruges det, at determinanten på grund af singularitetsbetingelsen skal være lig med 0: ${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {F}}$

${\ displaystyle \ det (\ mathbf {F}) = \ det (\ alpha \ mathbf {F} _ {1} + (1- \ alpha) \ mathbf {F} _ {2}) = 0.}$

Denne generelt kubiske ligning har - hvis den ikke degenererer i en kvadratisk ligning - mindst en og højst tre reelle løsninger . En grundlæggende matrix kan beregnes med hver løsning . Hvis der findes flere løsninger, kræves der yderligere point for at bestemme en unik løsning. Løsningen vælges, hvor den epipolære ligning også er opfyldt for andre punkter eller er omtrent opfyldt i tilfælde af måleunøjagtigheder i koordinaterne. ${\ displaystyle \ alpha}$${\ displaystyle \ alpha}$

Hvis det er, er det kubiske udtryk lig med nul, så det er en kvadratisk ligning. Denne ligning har højst to reelle løsninger til , men den kan ikke have nogen reel løsning. Men da matrixens determinant forsvinder, er den ental og derfor en løsning for den grundlæggende matrix, der søges, så i alt en til tre grundlæggende matricer kan findes som en løsning. Alternativt kan matrixen ganges med −1. En kubisk ligning med opløsningen opnås derefter igen . Af numeriske årsager kan denne procedure også anvendes, hvis mængden af ​​er meget stor. ${\ displaystyle \ det (\ mathbf {F} _ {1} - \ mathbf {F} _ {2}) = 0}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha}$${\ displaystyle \ mathbf {F} = \ mathbf {F} _ {1} - \ mathbf {F} _ {2}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {F} _ {2}}$${\ displaystyle \ alpha = {\ tfrac {1} {2}}}$${\ displaystyle \ alpha}$

8-punkts algoritme

Normalt er der mere end 7-punkts korrespondancer. 8-punktsalgoritmen beskrevet nedenfor kræver mindst 8 tilsvarende parpar, men flere punkter kan bruges. Longuet-Higgins kom op med ideen til denne proces.

I det første trin overvejes kun ligningssystemet uden at tage betingelsen i betragtning. I det ideelle tilfælde har matrixen rang 8, men i praksis er dette ikke tilfældet med mere end 8 point på grund af måleunøjagtigheder, så løsningen ikke kan bestemmes ud fra nullrummet af . I stedet findes løsningen ved hjælp af metoden med mindst kvadrat eller ved at bestemme egenværdier . Ved at bruge flere punkter, end der er nødvendige for en klar løsning, kan det også kontrolleres, om der er forkert korrespondance eller andre afvigelser . ${\ displaystyle \ mathbf {A} \ mathbf {f} = \ mathbf {0}}$${\ displaystyle \ det (\ mathbf {F}) = 0}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {A}}$

Metoden med mindste kvadrat bestemmes at være minimal. Da kun en faktor er entydig, skal der indføres en betingelse, f.eks. B. ved at indstille et element lig med 1. Problemet her er, at dette ikke kan være et element, der er 0 eller meget lille, hvilket ikke er kendt på forhånd. Der er dog flere måder at prøve. Den anden metode minimerer også , men med betingelsen . Dette fører til, at løsningen er egenvektoren for matrixens mindste egenværdi . ${\ displaystyle \ mathbf {f}}$${\ displaystyle \ | \ mathbf {A} \ mathbf {f} \ |}$${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {f}}$${\ displaystyle \ | \ mathbf {A} \ mathbf {f} \ |}$${\ displaystyle \ | \ mathbf {f} \ | = 1}$${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {A} ^ {\ text {T}} \ mathbf {A}}$

Den grundlæggende matrix dannet ud fra opløsningen er generelt ikke ental. Derfor skal denne betingelse være opfyldt i et andet trin. Til dette formål ved en enestående værdi nedbrydning i demonteret. er en diagonal matrix, der indeholder entalværdierne. Den mindste er sat lig med 0, og derefter den grundlæggende matrix beregnes fra matrixerne , og igen. Da en entalværdi nu er lig med 0, opfylder den grundlæggende matrix singularitetsbetingelsen. ${\ displaystyle \ mathbf {f}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {F}}$${\ displaystyle \ mathbf {F} = \ mathbf {U} \ mathbf {S} \ mathbf {V} ^ {\ text {T}}}$${\ displaystyle \ mathbf {S}}$${\ displaystyle \ mathbf {U}}$${\ displaystyle \ mathbf {S}}$${\ displaystyle \ mathbf {V}}$

8-punktsalgoritmen er en enkel metode til bestemmelse af den grundlæggende matrix, men den er modtagelig for måleunøjagtigheder og forkerte korrespondancer. Dette skyldes det faktum, at den grundlæggende matrixs singularitetsbetingelse først er opfyldt bagefter, og at den minimerede størrelse ikke har nogen fysisk betydning. Der er andre metoder, der ikke har disse ulemper. Disse metoder er imidlertid mere komplekse og bruges mindre ofte i praksis. ${\ displaystyle \ | \ mathbf {A} \ mathbf {f} \ |}$

Automatisk beregning

Automatisk beregning af den epipolære geometri er særlig nødvendig for maskinens syn, da f.eks. Autonome robotter skal handle uden menneskelig hjælp. For at gøre dette bestemmes et antal tilsvarende punkter i det første trin. Dette gøres ved hjælp af en interesseoperatør , som kan bruges til at lokalisere fremtrædende punkter i et billede. Når disse er fundet, bestemmes for hvert punkt i det første billede det nærmeste i det andet billede. En korrespondanceanalyse giver et mål for ligheden. På grund af de forskellige perspektiver, som de to kameraer ser på scenen, af lignende billeddetaljer, der ikke repræsenterer det samme objekt, og af billedstøj , indeholder sættet med tilsvarende punkter i praksis et større antal forkerte tildelinger og kan derfor ikke bruges til at beregne den grundlæggende matrix, der skal bruges direkte.

De følgende illustrationer viser en kirke taget fra to synspunkter. Den anden kameraposition er længere til højre og er lidt længere væk fra kirketårnet end den første. Figur 1 og 2 viser fremtrædende punkter, og figur 3 resultatet af korrespondanceanalysen, hvor lignende billedsektioner blev sammenlignet med hinanden - uden at tage højde for optagelsesgeometrien. Det kan tydeligt ses, at ikke al korrespondance blev identificeret korrekt. Dette er ikke tilfældet især inden for træernes område, da grenene alle har en lignende form og lysstyrke, og korrespondanceanalysen derfor fører til forkerte resultater. F.eks. Findes korrespondancer med fremtrædende punkter i træet til højre i det andet billede, skønt det ikke er synligt i det andet billede.

• Korrespondanceanalyse
• 

  1. Venstre billede med fremtrædende punkter.

• 

  2. Højre billede med fremtrædende punkter.

• 

  3. Formodet korrespondance som vektorer

Før beregningen skal fejlallokeringer udelukkes ved hjælp af egnede metoder til adskillelse og eliminering af afvigende. Den såkaldte RANSAC-algoritme bruges ofte til dette. Denne algoritme kan registrere fejlallokeringer i punkterne. Anvendt til beregningen af består den af ​​følgende trin: ${\ displaystyle \ mathbf {F}}$

1. Vælg tilfældigt 7 eller 8-punkts korrespondance fra datapunkterne. Dette gøres i forventning om, at denne korrespondance er fri for fejl.
2. Bestem ud fra den valgte korrespondance ved hjælp af 7- eller 8-punkts algoritmen .${\ displaystyle \ mathbf {F}}$
3. Bestem alle tilsvarende punkter, for hvilke der gælder: og gem dem. Tærskelværdien er nødvendig, fordi den epipolære ligning næsten aldrig nøjagtigt er opfyldt på grund af måle- og beregningsunøjagtigheder . Jo flere par punkter tilfredsstiller uligheden, desto mere sandsynligt indeholder de oprindeligt valgte punkter ingen fejlallokeringer.${\ displaystyle \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf {Fx} _ {1} \ leq \ epsilon}$${\ displaystyle \ epsilon}$${\ displaystyle \ mathbf {x} _ {2} ^ {\ text {T}} \ mathbf {Fx} _ {1} = 0}$
4. Gentag trin 1-3 så ofte, at der er en tilstrækkelig høj sandsynlighed for, at de tilfældigt valgte punktkorrespondancer ikke indeholder nogen fejl.

Den grundlæggende matrix bestemmes derefter ved hjælp af det største antal parpar fra trin 3 og 8-punktsalgoritmen. En korrespondanceanalyse kan derefter udføres igen, hvor den beregnede grundmatrix anvendes (som beskrevet, søgeområdet for tilsvarende punkter reduceres derved til den epipolære linje), og en lavere værdi accepteres for graden af ​​lighed. Disse sidste to trin kan gentages iterativt, indtil antallet af korrespondancer er stabilt. ${\ displaystyle \ mathbf {F}}$

De følgende to repræsentationer illustrerer resultatet. De accepterede korrespondancer er vist i figur 1 som røde vektorer. I figur 2 vises valgte punkter og deres epipolære linjer i det rigtige billede. Korrekt tildelte fremtrædende punkter og deres epipolære linjer vises med rødt. Punkt i korrespondanceanalysen, som ikke opfylder den epipolære ligning, for hvilken punktet i det rigtige billede ikke ligger på den tilsvarende epipolære linje, vises med grønt. Forkert korrespondance vises med blåt. Selvom disse punkter opfylder den epipolære ligning og viser lignende billeddetaljer, er de ikke billedpunkter med det samme objektpunkt. Epipolen i det højre billede er skæringspunktet mellem de epipolære linjer og er til venstre uden for billedet.

• Resultat af beregningen
• 

  1. Korrespondance (rød) ifølge RANSAC, der bruges til beregning. ${\ displaystyle \ mathbf {F}}$

• 

  2. Nogle epipolære linjer, beregnet med . ${\ displaystyle \ mathbf {F}}$

særlige tilfælde

Særlige tilfælde af epipolar geometri
Til venstre kamera-objektkonfigurationen, til højre de to overlejrede kamerabilleder a og b med de epipolære linjer (rød).

Med visse kameraers positioner til hinanden kan der være særlige tilfælde. To arrangementer er relevante i praksis, især med hensyn til maskinsyn:

1. Hvis de to billedplaner af kameraerne A og B (med samme kammerkonstant ) er i et plan, dvs. hvis optagelsesretningerne er nøjagtigt parallelle med hinanden, skifter epipolerne til uendelig, og de epipolære linjer bliver familier af lige linjer. Brug af homogene koordinater gør det særligt let at behandle disse punkter i uendelig grad. I figuren er de epipolære linjer i kuglecentrene og tangenterne nøjagtigt vandrette. Denne konfiguration - kendt som  stereonormalt tilfælde - kan ofte findes omtrent i luftfotogrammetri og stereosyn, og når man søger efter korrespondance, har den fordelen, at den epipolære geometri er kendt på grund af de vandrette epipolære linjer og kun en billedkorrespondens skal søges i det vandrette plan, dvs. langs en linje af pixels til digitale kameraer . Jo tættere objekterne er på kameraerne, jo længere væk pixelerne er fra positionen i det andet billede: Denne parallakseffekt angiver afstanden mellem objekterne, kort sagt: den tredje dimension.
   Dette specielle tilfælde gælder også for menneskets syn: På trods af øjnets bevægelighed er det næsten umuligt at rette øjnene i retninger, der ikke er i samme plan som linjen, der forbinder øjnene. Du kan kun se efter korrespondance i sådanne retninger.
2. Hvis de to kameraer er foran hinanden, dvs. hvis de forskydes mod hinanden i synsretningen, skifter epipolerne ind i midten af ​​billedet; de epipolære linjer løber derfor udad i en stjerneform startende fra midten af ​​billedet. Denne konfiguration forekommer ofte med mobile robotter, når et enkelt kamera er orienteret i kørselsretningen og tager billeder på forskellige tidspunkter. Billedkorrespondancerne søges derefter i de på hinanden følgende billeder af kameraet. Også i dette tilfælde kan afstanden fra kamerapositionen bestemmes ud fra parallakseffekten. Når robotten panorerer kameraet i en kurve, bevæger epipolerne sig vandret, foran til ydersiden af ​​kurven og bagud indefra, så specialtilfældet ikke længere eksisterer.

I disse specielle tilfælde er korrespondance-søgningen forenklet, fordi den epipolære geometri er kendt. I konfigurationer, hvor kameravisninger kun er omtrent parallelle, kan denne tilstand etableres ved efterfølgende beregning af normale billeder.

Udvidelse til mere end to billeder

Trifokal geometri

Den trifokale geometri er udvidelsen af ​​den epipolære geometri til tre billeder. Hvis placeringen af ​​et objektpunkt er angivet i to billeder, er dets position i det tredje billede skæringspunktet mellem de to epipolære linjer i dette billede. I modsætning til billedparret er der et klart resultat, forudsat at punktet ikke er i trifokalplanet (det plan, der er dannet ud fra de tre projektionscentre), eller de tre projektionscentre er på en linje. Arrangementet, hvor et 3D-punkt ligger på trifokalplanet, kaldes et entalssag .

Det er muligt at udvide den epipolære geometri til mere end tre billeder. I praksis er dette kun almindeligt for fire visninger. Den såkaldte quadrifokale tensor findes her, som beskriver forholdet mellem pixels og linjer mellem disse billeder. Imidlertid blev der ikke undersøgt nogen matematiske sammenhænge for mere end fire visninger, da kompleksiteten af ​​modelleringen og beregningen er signifikant højere, og i de fleste applikationer, startende med det femte kamera, er den yderligere informationsgevinst kun lille.

Afvigelser fra modellen til pinhole-kameraet

Det beskrevne forhold mellem tilsvarende billedpunkter, som kan beskrives fuldstændigt af den grundlæggende matrix, gælder kun for fotografier, der kan modelleres af et pinhole-kamera. Hvis der for eksempel forekommer forvrængninger i billeddannelsen på billedplanet, eller hvis billedoverfladen ikke er et plan, skal disse afvigelser tages i betragtning i den epipolære geometri. Især er de epipolære linjer, hvorpå billedpunktet, der svarer til et billedpunkt i det første billede, skal søges i det andet billede, ikke lige linjer.

Forvrængning

Når forvrængning er enhver afvigelse fra pinhole-kameraets ideelle billedmodel. Det stammer fra den asymmetriske position af blænden i en linse og fører til, at reproduktionsskalaen i billedet ændres systematisk. Linser med en symmetrisk struktur har normalt ingen (radialt symmetrisk) forvrængning. For andre linser og tilsvarende nøjagtighedskrav skal forvrængningen tages i betragtning. Forvrængningen kan ofte modelleres som radial forvrængning ; H. det øges med afstanden fra forvrængningens centrum (normalt nær midten af ​​billedet).

Hvis et kamera kalibreres i overensstemmelse hermed, og forvrængningen er kendt, kan billederne korrigeres. Disse korrigerede billeder kan derefter bruges som med forvrængningsfrie billeder.

Under visse betingelser kan forvrængningen tages i betragtning i en udvidet grundlæggende matrix. Der antages en forvrængning for hvert billede, som kan beskrives ved en (ukendt) parameter i hvert tilfælde, og som svarer til udskiftningen af ​​den flade billedoverflade med en firkantet overflade i et tredimensionelt projektivt rum. Forholdet mellem to tilsvarende punkter beskrives derefter af en grundlæggende matrix med 9 frihedsgrader.${\ displaystyle 4 \ gange 4}$

Panoramakameraer

I tilfælde af panoramakameraer, der tillader optagelser med en stor synsvinkel , kan optagelsesgeometrien ikke modelleres af et pinhole-kamera med en flad billedoverflade. Beskrivelsen af ​​den epipolære geometri afhænger af typen af ​​panoramakamera. Hvis kameraet f.eks. Består af et pinhole-kamera og et hyperbolsspejl , danner de epipolære linjer koniske sektioner.

fodnote

1. ↑ ^{a b} En lige linje defineres i homogene koordinater ved en homogen lineær ligning mellem de homogene koordinater, det vil sige alle punkter, der tilfredsstiller ligelinjen ligning ligger på den lige linie bestemt af . Punkterne på den lige linje, som indeholder to forskellige punkter, og defineres af det rumlige produkt .${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {l} ^ {\ text {T}} \ mathbf {x} = 0}$${\ displaystyle \ mathbf {l}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {x} _ {1}}$${\ displaystyle \ mathbf {x} _ {2}}$ ${\ displaystyle \ det (\ mathbf {x}, \, \ mathbf {x} _ {1}, \, \ mathbf {x} _ {2}) \, = \, (\ mathbf {x} _ {1 } \ times \ mathbf {x} _ {2}) ^ {\ text {T}} \ mathbf {x} \, = \, 0}$

litteratur

• Richard Hartley, Andrew Zisserman: Multiple View Geometry in Computer Vision . 2. udgave. Cambridge University Press, 2004, ISBN 0-521-54051-8 . 
• Olivier Faugeras: Tredimensionelt computersyn - Et geometrisk synspunkt . MIT Press, Cambridge (Massachusetts) 1993, ISBN 0-262-06158-9 . 
• Volker Rodehorst: Fotogrammetrisk 3D-rekonstruktion på tæt hold gennem automatisk kalibrering med projektiv geometri . wvb Wissenschaftlicher Verlag Berlin, 2004, ISBN 3-936846-83-9 . 
• Oliver Schreer: Stereoanalyse og billedsyntese . Springer, Berlin, 2008, ISBN 978-3-540-23439-5 . 
• Richard Hartley, Andrew Zisserman: Kapitel 9 fra Multiple View Geometry in computer vision. (PDF; 265 kB) 2007, adgang til den 18. august 2007 . 
• Zhengyou Zhang: Bestemmelse af den epipolære geometri og dens usikkerhed: En gennemgang. (PDF; 1,6 MB) 1996, adgang den 8. august 2007 . 
• Andrew Zisserman: MATLAB-funktioner til geometri med flere visninger. 2007, adgang til 14. august 2007 . 

Weblinks

• SRI International - Java-applets til at illustrere billeddannelseslove for et, to eller tre kameraer
• University of Siena - Epipolar Geometry Toolbox ( Matlab- rutiner)
• The Fundamental Matrix Song - En sang, der forklarer den grundlæggende matrix og epipolar geometri i en nøddeskal (af Daniel Wedge)

Individuelle beviser

1. ^ Karl Kraus, Peter Waldhäusl: Photogrammetrie, bind 1 . Ferd. Dümmler, Bonn 1997, ISBN 3-427-78646-3 . 
2. ↑ Ephrahim Garcia: Teknisk gennemgang af Team Cornells Spider DARPA Grand Challenge 2005 . 28. august 2005 ( darpa.mil [PDF; 1.3 MB ; adgang 23. juli 2012]). 
3. ↑ Sebastian Finsterwalder: De geometriske grundlæggende fotogrammetri . I: Årsrapport fra den tyske matematikerforening . bånd 6 , nr. 2 . Leipzig 1899, s. 1-41 .  ( Fuld tekst )
4. ↑ Horst von Sanden: Bestemmelsen af ​​nøglepunkterne i fotogrammetri (afhandling ved University of Göttingen) . Goettingen 1908. 
5. ↑ ^{a b} H. C. Longuet-Higgins: En computeralgoritme til rekonstruktion af en scene ud fra to projektioner . I: Natur . bånd 293 , 1981, s. 133-135 . 
6. ↑ TS Huang, OD Faugeras: Nogle egenskaber ved E-matrixen i to-visnings bevægelsesestimering . I: IEEE-transaktioner på mønsteranalyse og maskinintelligens . bånd 11 , 1989, s. 1310-1312 . 
7. ↑ BKP Horn: Relativ orientering . I: International Journal of Computer Vision . bånd 4 , 1990, s. 59-78 . 
8. ↑ T. Vieville, D. Lingrand: Brug af ental forskydninger til ukalibrerede monokulære synssystemer . I: Teknisk rapport 2678 INRIA . 1995. 
9. ↑ Zhengyou Zhang: Bestemmelse af den epipolære geometri og dens usikkerhed: En gennemgang. (PDF; 1,6 MB) 1996, adgang den 8. august 2007 . 
10. Ao Joao P. Barreto og Kostas Daniilidis: Grundlæggende matrix til kameraer med radial forvrængning . I: Proceedings of the Tiende IEEE International Conference on Computer Vision (ICCV'05) , 2005, s. 625–632 ( PDF ( Memento fra 29. juni 2010 i Internetarkivet ))

Denne artikel blev tilføjet til listen over fremragende artikler den 8. marts 2008 i denne version .