Én-trins proces

Ettrins fremgangsmåder tilnærme opløsningen (blå) af en begyndelsesværdi problem ved bestemmende punkter , etc., den ene efter den anden fra den givne startpunkt${\ displaystyle A_ {0}}$${\ displaystyle A_ {1}}$${\ displaystyle A_ {2}}$

I numerisk matematik er et-trinsmetoder ud over flertrinsmetoderne en stor gruppe beregningsmetoder til løsning af startværdiproblemer . Denne opgave, hvor en fælles differentialligning er givet sammen med en startbetingelse, spiller en central rolle i alle naturvidenskabelige og tekniske videnskaber og bliver stadig vigtigere, for eksempel inden for økonomi og samfundsvidenskab. Indledende værdiproblemer bruges til at analysere, simulere eller forudsige dynamiske processer.

Den navngivende grundlæggende idé med et-trins-metoden er, at de, startende fra det givne startpunkt, beregner tilnærmelsespunkter trin for trin langs den søgte løsning. Dermed bruger de kun den senest bestemte tilnærmelse til næste trin i modsætning til flertrinsmetoden, som også inkluderer punkter, der var længere tilbage i beregningen. Et-trinsmetoderne kan groft opdeles i to grupper: de eksplicitte metoder, der beregner den nye tilnærmelse direkte fra den gamle, og de implicitte metoder, hvor en ligning skal løses. Sidstnævnte er også velegnede til såkaldte stive startværdiproblemer.

Den enkleste og ældste et-trins metode, den eksplicitte Euler-metode , blev offentliggjort i 1768 af Leonhard Euler . Efter at en gruppe flertrinsprocesser var blevet præsenteret i 1883, udviklede Carl Runge , Karl Heun og Wilhelm Kutta omkring 1900 betydelige forbedringer af Eulers proces. Fra disse opstod den store gruppe af Runge-Kutta-processerne , som udgør den vigtigste klasse af et-trins processer. Yderligere udvikling i det 20. århundrede er for eksempel ideen om ekstrapolering , men frem for alt overvejelser for trinstørrelseskontrol, dvs. for valg af passende længder til de enkelte trin i en metode. Disse begreber danner grundlaget for at løse vanskelige startværdiproblemer, da de forekommer i moderne applikationer, effektivt og med den krævede nøjagtighed ved hjælp af computerprogrammer.

introduktion

Almindelige differentialligninger

Udviklingen af ​​differentieret og integreret beregning af den engelske fysiker og matematiker Isaac Newton og uafhængigt af den af ​​den tyske polymat Gottfried Wilhelm Leibniz i den sidste tredjedel af det 17. århundrede var en væsentlig drivkraft for matematiseringen af ​​videnskab i den tidlige moderne periode . Disse metoder udgjorde udgangspunktet for den matematiske analyse og er af central betydning i alle naturvidenskabelige og tekniske videnskaber. Mens Leibniz blev ledet af det geometriske problem med at bestemme tangenter til givne kurver til differentieret beregning, startede Newton fra spørgsmålet om, hvordan ændringer i en fysisk størrelse kan bestemmes på et bestemt tidspunkt.

For eksempel, når et legeme bevæger sig, er dets gennemsnitlige hastighed simpelthen den tilbagelagte afstand divideret med den tid, det tog. For at matematisk formulere kroppens aktuelle hastighed på et bestemt tidspunkt er det imidlertid nødvendigt med en grænseovergang: Man betragter korte længder , de tilbagelagte afstande og de tilhørende gennemsnitshastigheder . Hvis man lader tidsrummet konvergere til nul, og hvis gennemsnitshastighederne også nærmer sig en fast værdi , kaldes denne værdi den (øjeblikkelige) hastighed på det givne tidspunkt . Beskriver positionen af kroppen på det tidspunkt , så man skriver og navne på afledningen af . ${\ displaystyle v (t)}$${\ displaystyle t}$${\ displaystyle \ Delta t}$${\ displaystyle \ Delta x}$${\ displaystyle {\ tfrac {\ Delta x} {\ Delta t}}}$${\ displaystyle \ Delta t}$${\ displaystyle v (t)}$${\ displaystyle t}$${\ displaystyle x (t)}$${\ displaystyle t}$${\ displaystyle v (t) = x '(t)}$${\ displaystyle v}$${\ displaystyle x}$

Det afgørende skridt i retning af differentialligningsmodeller er nu det modsatte spørgsmål: I eksemplet med det bevægelige legeme er hastigheden kendt til enhver tid, og dens position skal bestemmes ud fra dette. Det er tydeligt, at kroppens udgangsposition også skal være kendt på et tidspunkt for at være i stand til klart at løse dette problem. Det er en funktion at søge, at den oprindelige betingelse med givne værdier og er opfyldt. ${\ displaystyle t}$${\ displaystyle v (t)}$${\ displaystyle x (t)}$${\ displaystyle t_ {0}}$${\ displaystyle x (t)}$${\ displaystyle x '(t) = v (t)}$${\ displaystyle x (t_ {0}) = x_ {0}}$${\ displaystyle t_ {0}}$${\ displaystyle x_ {0}}$

I eksemplet med bestemmelse af et legems position ud fra dets hastighed er afledningen af ​​den ønskede funktion udtrykkeligt angivet. Normalt er der dog det vigtige generelle tilfælde af almindelige differentialligninger for en krævet størrelse : Baseret på naturlovene eller modelantagelserne kendes et funktionelt forhold, der indikerer, hvordan afledningen af den funktion, der skal bestemmes, kan beregnes ud fra og fra den (ukendte) værdi . Derudover skal der igen være en indledende betingelse, der f.eks. Kan opnås ved en måling af den krævede variabel på et fast tidspunkt. Sammenfattende har vi følgende generelle type problem: Find den funktion, der indeholder ligningerne ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle y '(t)}$${\ displaystyle t}$${\ displaystyle y (t)}$${\ displaystyle y}$

${\ displaystyle y '(t) = f (t, y (t)), \ quad y (t_ {0}) = y_ {0}}$

hvor er en given funktion. ${\ displaystyle f}$

Den præsenterede løsning af Lorenz-tiltrækkers differentialligning er en meget kompliceret kurve i et tredimensionelt rum

Et simpelt eksempel er en størrelse, der vokser eksponentielt . Dette betyder, at den aktuelle ændring, dvs. afledningen, er proportional med sig selv. Så det gælder med en vækstrate og for eksempel en indledende tilstand . I dette tilfælde kan den løsning, du leder efter, allerede findes med elementær differensberegning og specificeret ved hjælp af den eksponentielle funktion : Den gælder . ${\ displaystyle y}$${\ displaystyle y '(t)}$ ${\ displaystyle y (t)}$${\ displaystyle y '(t) = \ lambda y (t)}$${\ displaystyle \ lambda}$${\ displaystyle y (0) = y_ {0}}$${\ displaystyle y}$${\ displaystyle y (t) = y_ {0} e ^ {\ lambda t}}$

Den funktion, der søges i en differentialligning, kan vurderes med vektor , dvs. for hver kan der være en vektor med komponenter. Man taler derefter om et dimensionelt differentialligningssystem. I tilfælde af et bevægeligt legeme er dets position i det dimensionelle euklidiske rum og dets hastighed på det tidspunkt . Differentialligningen specificerer derfor hastigheden på den søgte bane med retning og størrelse på hvert punkt i tid og rum . Selve stien skal beregnes ud fra dette. ${\ displaystyle y}$${\ displaystyle t}$${\ displaystyle y (t) = (y_ {1} (t), \ dotsc, y_ {d} (t))}$${\ displaystyle d}$${\ displaystyle d}$${\ displaystyle y (t)}$${\ displaystyle d}$${\ displaystyle y '(t)}$${\ displaystyle t}$

Grundlæggende idé om et-trins processen

Med den enkle differentialligning af eksponentiel vækst betragtet som et eksempel ovenfor kunne løsningsfunktionen specificeres direkte. Generelt er dette ikke længere muligt med mere komplekse problemer. Under visse yderligere betingelser kan man så for funktionen vise, at der findes en entydigt bestemt løsning af det oprindelige værdiproblem; Dette kan dog ikke længere beregnes eksplicit ved hjælp af analysemetoder (såsom adskillelse af variabler , en eksponentiel tilgang eller variation af konstanterne ). I dette tilfælde kan numeriske metoder bruges til at tilnærme den ønskede løsning. ${\ displaystyle f}$

Metoderne til den numeriske løsning af startværdiproblemer ved almindelige differentialligninger kan groft opdeles i to store grupper: et-trins- og flertrinsmetoden. Begge grupper har det til fælles at de gradvist beregner tilnærmelser for de ønskede funktionsværdier på punkter . Den definerende egenskab ved et-trins-metoden er, at kun den "aktuelle" tilnærmelse bruges til at bestemme den følgende tilnærmelse . I modsætning hertil er tidligere beregnede tilnærmelser også inkluderet i tilfælde af flertrinsmetoder; en tretrins metode ville derfor f.eks. også bruge og bestemme den nye tilnærmelse . ${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$${\ displaystyle y (t_ {0}), y (t_ {1}), y (t_ {2}), \ dotsc}$${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots}$${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle y_ {j-1}}$${\ displaystyle y_ {j-2}}$${\ displaystyle y_ {j + 1}}$

To trin i den eksplicitte Euler-metode

Den enkleste og mest basale et-trins metode er den eksplicitte Euler-metode , som den schweiziske matematiker og fysiker Leonhard Euler præsenterede i sin lærebog Institutiones Calculi Integralis i 1768 . Ideen med denne metode er at tilnærme den løsning, der søges af en stykkevis lineær funktion, hvor hældningen af ​​den lige linje er givet i hvert trin fra punkt til punkt . Mere præcist: Problemet giver allerede en værdi for den søgte funktion, nemlig . Men afledningen på dette tidspunkt er også kendt, fordi den gælder . Tangenten til grafen for opløsningsfunktionen kan således bestemmes og bruges som en tilnærmelse. På dette tidspunkt er der en trinstørrelse${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle y (t_ {0}) = y_ {0}}$${\ displaystyle y '(t_ {0}) = f (t_ {0}, y_ {0})}$${\ displaystyle t_ {1}> t_ {0}}$${\ displaystyle h_ {0}: = t_ {1} -t_ {0}}$

${\ displaystyle y (t_ {1}) \ approx y_ {0} + h_ {0} f (t_ {0}, y_ {0}) =: y_ {1}}$.

Denne procedure kan nu fortsættes i de følgende trin. Samlet set resulterer dette i beregningsreglen for den eksplicitte Euler-metode

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j}, y_ {j}), \ quad j = 0,1,2, \ dotsc}$

med trinstørrelserne .${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

Den eksplicitte Euler-metode er udgangspunktet for adskillige generaliseringer, hvor skråningen erstattes af skråninger, der tilnærmer løsningen mellem punkterne og mere præcist. Den implicitte Euler-metode, der bruges som hældning, giver en yderligere idé til et-trins metoder . Ved første øjekast ser dette valg ikke ud til at være passende, da det er ukendt. Ligningen opnås nu som et proceduretrin ${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle t_ {j + 1}}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} f (t_ {j + 1}, y_ {j + 1})}$

hvorfra (om nødvendigt ved en numerisk metode) kan beregnes. Hvis for eksempel det aritmetiske gennemsnit af skråningerne af den eksplicitte og den implicitte Euler-metode vælges som hældningen, opnås den implicitte trapezmetode . En eksplicit metode kan opnås ud fra dette, for eksempel hvis man tilnærmer det ukendte på højre side af ligningen ved at tilnærme den eksplicitte Euler-metode, den såkaldte Heun-metode . Alle disse procedurer og alle andre generaliseringer har den grundlæggende idé om et-trins-proceduren til fælles: trinnet ${\ displaystyle y_ {j + 1}}$${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi}$

med en skråning, der kan afhænge af , og og (i tilfælde af implicitte metoder) af. ${\ displaystyle \ Phi}$${\ displaystyle t_ {j}}$${\ displaystyle y_ {j}}$${\ displaystyle h_ {j}}$${\ displaystyle y_ {j + 1}}$

definition

Med hensyn til indledningen i denne artikel kan konceptet med et-trins-proceduren defineres som følger: Vi leder efter løsningen på det oprindelige værdiproblem ${\ displaystyle y}$

${\ displaystyle y '(t) = f (t, y (t))}$, .${\ displaystyle \ quad y (t_ {0}) = y_ {0}}$

Det antages, at løsningen

${\ displaystyle y \ colon I \ to \ mathbb {R} ^ {d}}$

eksisterer i et givet interval og bestemmes entydigt. er ${\ displaystyle I = [t_ {0}, T]}$

${\ displaystyle t_ {0} <t_ {1} <t_ {2} <\ ldots <t_ {n} = T}$

Mellemliggende punkter i intervallet og de tilhørende trinstørrelser, så betyder det igennem ${\ displaystyle I}$${\ displaystyle h_ {j} = t_ {j + 1} -t_ {j}}$

${\ displaystyle y_ {j + 1} = y_ {j} + h_ {j} \ Phi (t_ {j}, y_ {j}, y_ {j + 1}, h_ {j})}$, ${\ displaystyle \ quad j = 0, \ dotsc, n-1}$

givne procedurer et-trins procedure med procedurefunktion . Hvis det ikke afhænger af, kaldes det en eksplicit procedure i et trin . Ellers skal en ligning for løses i hvert trin, og proceduren kaldes implicit .${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle y_ {j + 1}}$${\ displaystyle j}$${\ displaystyle y_ {j + 1}}$

Konsistens og konvergens

Konvergensrækkefølge

Global fejl i forskellige trinstørrelser til tre et-trinsmetoder. I et dobbeltlogaritmisk plot vises forholdet omtrent lineært, skråningerne svarer til konvergensordren 1, 2 og 4.${\ displaystyle h}$

For en praktisk et-trins metode skal de beregnede gode tilnærmelser til værdierne for den nøjagtige opløsning være på det punkt . Da mængderne generelt er -dimensionelle vektorer, måles kvaliteten af ​​denne tilnærmelse med en vektornorm som fejlen ved punktet . Det er ønskeligt, at disse fejl hurtigt konvergerer til nul for alle, hvis trinstørrelserne får lov til at konvergere til nul. For også at dække tilfældet med ikke-konstante trinstørrelser definerer man dette mere præcist som det maksimale af de anvendte trinstørrelser og overvejer opførelsen af ​​den maksimale fejl på alle punkter sammenlignet med styrker af . Det siges, at et-trins-proceduren til løsning af det givne startværdiproblem har konvergensrækkefølgen, hvis estimatet ${\ displaystyle y_ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle y}$${\ displaystyle t_ {j}}$${\ displaystyle d}$${\ displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle t_ {j}}$${\ displaystyle j}$${\ displaystyle h}$${\ displaystyle t_ {j}}$${\ displaystyle h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ max _ {j = 0, \ dotsc, n} \ | y_ {j} -y (t_ {j}) \ | \ leq Ch ^ {p}}$

holder for alle tilstrækkeligt små med en konstant, der er uafhængig af .${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

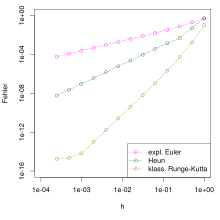
Rækkefølgen af ​​konvergens er den vigtigste parameter til sammenligning af forskellige et-trins procedurer. En metode med en højere orden af ​​konvergens leverer generelt en mindre total fejl for en given trinstørrelse, eller omvendt er færre trin nødvendige for at opnå en given nøjagtighed. I tilfælde af en metode med kan det forventes, at hvis trinstørrelsen halveres, vil fejlen kun blive omtrent halveret. I tilfælde af en metode i rækkefølgen af ​​konvergens kan man dog antage, at fejlen reduceres med omtrent faktoren . ${\ displaystyle p}$${\ displaystyle p = 1}$${\ displaystyle p = 4}$${\ displaystyle {\ bigl (} {\ tfrac {1} {2}} {\ bigr)} ^ {4} = {\ tfrac {1} {16}}}$

Global og lokal fejl

Fejlene, der overvejes i definitionen af ​​konvergensrækkefølgen , består af to individuelle komponenter på en måde, der oprindeligt synes kompliceret: Selvfølgelig afhænger de på den ene side af den fejl, proceduren laver i et enkelt trin, idet ukendt hældning af den søgte funktion erstattes af den omtrentlige procedurefunktion. På den anden side skal det også tages i betragtning, at startpunktet for et trin generelt ikke allerede falder sammen med det nøjagtige udgangspunkt ; fejlen efter dette trin afhænger også af alle fejl, der allerede er foretaget i de foregående trin. På grund af den ensartede definition af et-trins-proceduren, som kun adskiller sig i valg af procedurefunktionen , kan det bevises, at man (under visse tekniske forhold ) kan udlede konvergensrækkefølgen direkte fra fejlrækkefølgen i et enkelt trin, den såkaldte konsistensrækkefølge . ${\ displaystyle \ | y_ {j} -y (t_ {j}) \ |}$${\ displaystyle (t_ {j}, y_ {j})}$${\ displaystyle (t_ {j}, y (t_ {j}))}$${\ displaystyle \ Phi}$${\ displaystyle \ Phi}$

Begrebet konsistens er et generelt og centralt begreb i moderne numerisk matematik. Mens man undersøger, hvor godt de numeriske tilnærmelser passer til den nøjagtige løsning under konvergensen af ​​en procedure, når det kommer til konsistens, for at sige det enkelt, stiller man det "modsatte" spørgsmål: Hvor godt opfylder den nøjagtige løsning den proceduremæssige specifikation? I denne generelle teori fastslås det, at en metode er konvergent, hvis og kun hvis den er konsistent og stabil . For at forenkle notationen skal det under følgende overvejelse antages, at en eksplicit procedure i et trin

${\ displaystyle y_ {j + 1} = y_ {j} + h \ Phi (t_ {j}, y_ {j}, h)}$

med en konstant trinstørrelse . Den sande løsning definerer den lokale klipningsfejl (også kaldet lokal procedurefejl ) som${\ displaystyle h}$${\ displaystyle t \ mapsto y (t)}$${\ displaystyle \ eta}$

${\ displaystyle \ eta (t, h) = y (t) + h \ Phi (t, y (t), h) -y (t + h)}$.

Så man antager, at den nøjagtige løsning er kendt, starter et procestrin på det tidspunkt og danner forskellen til den nøjagtige løsning på det punkt . Dette definerer: En et-trins procedure har rækkefølgen af konsistens, hvis estimatet ${\ displaystyle (t, y (t))}$${\ displaystyle t + h}$ ${\ displaystyle p \ geq 1}$

${\ displaystyle \ | \ eta (t, h) \ | \ leq Ch ^ {p + 1}}$

holder for alle tilstrækkeligt små med en konstant, der er uafhængig af . ${\ displaystyle h}$${\ displaystyle h}$${\ displaystyle C> 0}$

Den mærkbare forskel mellem definitionerne af rækkefølgen af ​​konsistens og rækkefølgen af ​​konvergens er kraften i stedet for . Dette kan tydeligt fortolkes på en sådan måde, at en styrke i trinstørrelsen ”går tabt” under overgangen fra lokal til global fejl. Følgende sætning, som er central for teorien om et-trins-proceduren, gælder:${\ displaystyle h ^ {p + 1}}$${\ displaystyle h ^ {p}}$

Hvis procesfunktionen er Lipschitz kontinuerlig, og den tilknyttede et-trins proces har rækkefølgen af ​​konsistens , så har den også rækkefølgen af ​​konvergens .${\ displaystyle \ Phi}$ ${\ displaystyle p}$${\ displaystyle p}$

Lipschitz-kontinuiteten i procesfunktionen som et yderligere krav til stabilitet er generelt altid opfyldt, hvis funktionen fra differentialligningen i sig selv er Lipschitz kontinuerlig. Dette krav skal alligevel antages for de fleste applikationer for at garantere den entydige løsning på det oprindelige værdiproblem. Ifølge sætningen er det tilstrækkeligt at bestemme konsistensrækkefølgen for en et-trins procedure. I princippet kan dette opnås ved en Taylor-udvidelse af beføjelser til . I praksis bliver de resulterende formler til højere ordrer meget komplicerede og forvirrende, så der kræves yderligere koncepter og notationer.${\ displaystyle f}$${\ displaystyle \ eta (t, h)}$${\ displaystyle h}$

Stivhed og A-stabilitet

Konvergensrækkefølgen for en metode er en asymptotisk sætning, der beskriver tilnærmelsenes opførsel, når trinstørrelsen konvergerer til nul. Det siger dog intet om, hvorvidt metoden faktisk beregner en anvendelig tilnærmelse til en given fast trinstørrelse. Charles Francis Curtiss og Joseph O. Hirschfelder beskrev først i 1952, at dette faktisk kan være et stort problem med visse typer indledende værdiproblemer . De havde observeret, at løsningerne i nogle systemer med differentialligninger af kemisk reaktionskinetik ikke kunne beregnes ved hjælp af eksplicit numeriske metoder, og de kaldte dem sådanne oprindelige værdiproblemer "stive". Der er adskillige matematiske kriterier til bestemmelse af, hvor stiv et givet problem er. Det er klart, at stive startværdiproblemer for det meste er systemer med differentialligninger, hvor nogle komponenter bliver konstant meget hurtigt, mens andre komponenter kun ændrer sig langsomt. En sådan adfærd forekommer typisk ved modellering af kemiske reaktioner. Den mest nyttige definition af stivhed til praktisk anvendelse er: Et indledende værdiproblem er stiv, hvis man skulle vælge trinstørrelsen "for lille" for at opnå en anvendelig løsning med en eksplicit et-trins metode. Sådanne problemer kan kun løses med implicitte metoder.

For at beregne en eksponentielt faldende opløsning (blå) er den eksplicitte Euler-metode (rød) fuldstændig ubrugelig, hvis trinstørrelsen er for stor; den implicitte Euler-metode (grøn) bestemmer løsningen kvalitativt korrekt for enhver trinstørrelse.

Denne effekt kan illustreres mere præcist ved at undersøge, hvordan de enkelte metoder håndterer eksponentielt henfald . For at gøre dette, overveje den test ligning i henhold til den svenske matematiker Germund Dahlquist

${\ displaystyle y '(t) = \ lambda y (t), \ quad y (0) = 1}$

med den eksponentielt faldende opløsning . Det grafiske modsatte viser - som et eksempel på den eksplicitte og implicitte Euler-metode - den typiske opførsel af disse to grupper af metoder i dette tilsyneladende enkle indledende værdiproblem: Hvis man bruger for stor trinstørrelse i en eksplicit metode, så svingende værdier resultat, som er i opbygningen af ​​beregningen og bevæger sig længere og længere væk fra den nøjagtige løsning. Implicitte metoder beregner derimod typisk løsningen kvalitativt korrekt for alle trinstørrelser, nemlig som en eksponentielt faldende sekvens af omtrentlige værdier.${\ displaystyle \ lambda <0}$${\ displaystyle y (t) = e ^ {\ lambda t}}$

Ovenstående testligning betragtes også noget mere generelt for komplekse værdier på . I dette tilfælde svinger opløsningerne, hvis amplitude forbliver afgrænset, hvis det er relevant, dvs. den reelle komponent på mindre end eller lig med 0. Dette gør det muligt at formulere en ønskelig egenskab ved et-trins metoder, der skal bruges til stive startværdiproblemer: den såkaldte A-stabilitet. En metode kaldes A-stabil, hvis den anvendes til testligningen for en hvilken som helst trinstørrelse og beregnes for alle med en sekvens af tilnærmelser, som (som den sande løsning) forbliver begrænset. Den implicitte Euler-metode og den implicitte trapezmetode er de enkleste eksempler på A-stabile et-trins-metoder. På den anden side kan det vises, at en eksplicit procedure aldrig kan være A-stabil.${\ displaystyle \ lambda}$${\ displaystyle \ operatorname {Re} (\ lambda) \ leq 0}$${\ displaystyle \ lambda}$${\ displaystyle h> 0}$${\ displaystyle \ lambda}$${\ displaystyle \ operatorname {Re} (\ lambda) \ leq 0}$${\ displaystyle y_ {0}, y_ {1}, y_ {2}, \ dotsc}$

Særlige procedurer og klasser af procedurer

Nogle et-trins procedurer i sammenligning

Enkle procedurer i rækkefølge 1 og 2

Som den franske matematiker Augustin-Louis Cauchy beviste omkring 1820, har Euler-metoden rækkefølgen af ​​konvergens 1. Hvis skråningerne af den eksplicitte Euler-metode og den implicitte Euler-metode , som de findes i de to slutpunkter i et trin, kan være gennemsnit håber at få en bedre tilnærmelse over hele intervallet. Faktisk kan det bevises, at den implicitte trapezformede metode således opnås${\ displaystyle f (t_ {j}, y_ {j})}$${\ displaystyle f (t_ {j + 1}, y_ {j + 1})}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Big (} f (t_ {j}, y_ {j}) + f (t_ {j + 1 }, y_ {j + 1}) {\ Big)}}$

konvergensrækkefølgen har 2. Denne metode har meget gode stabilitetsegenskaber, men er implicit, så en ligning for skal løses i hvert trin . Hvis denne størrelse tilnærmes på højre side af ligningen ved hjælp af den eksplicitte Euler-metode, resulterer Heuns eksplicit metode${\ displaystyle y_ {j + 1}}$

${\ displaystyle y_ {j + 1} = y_ {j} + {\ frac {h} {2}} {\ Big (} f (t_ {j}, y_ {j}) + f {\ big (} t_ {j + 1}, y_ {j} + hf (t_ {j}, y_ {j}) {\ big)} {\ Big)}}$,

som også har konvergensrækkefølgen 2. En anden simpel eksplicit metode i rækkefølge 2, den forbedrede Euler-metode , kan opnås ved at overveje følgende: En "middel" hældning i procestrinet ville være hældningen af ​​opløsningen i midten af ​​trinnet, dvs. på det punkt . Da løsningen imidlertid er ukendt, tilnærmes den dog med et eksplicit Euler-trin med halv trinstørrelse. Den proceduremæssige regel er resultatet ${\ displaystyle y}$${\ displaystyle t_ {j} + {\ tfrac {h} {2}}}$

${\ displaystyle y_ {j + 1} = y_ {j} + hf {\ big (} t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2 }} f (t_ {j}, y_ {j}) {\ big)}}$.

Disse et-trins metoder i rækkefølge 2 blev alle offentliggjort i 1895 af den tyske matematiker Carl Runge som forbedringer af Euler-metoden .

Runge-Kutta metode

Den klassiske fjerde-ordens Runge-Kutta-metode er i gennemsnit fire hjælpeskråninger (rød) i hvert trin

Ovennævnte ideer til enkle et-trinsmetoder fører, hvis de generaliseres yderligere, til den vigtige klasse af Runge-Kutta-metoder. For eksempel kan Heuns metode præsenteres mere tydeligt som følger: Først beregnes en hjælpestigning , nemlig hældningen af ​​den eksplicitte Euler-metode. Dette bestemmer en anden ekstra hældning her . Den faktisk anvendte procesgradient resulterer derefter som et vægtet gennemsnit af hjælpegradienterne i Heun-metoden . Denne procedure kan generaliseres til mere end to hjælpeskråninger. En -trins Runge-Kutta-metode beregner først hjælpeforløb ved at evaluere dem på passende punkter og derefter som et vægtet gennemsnit. I tilfælde af en eksplicit Runge-Kutta-metode beregnes hjælpeskråningerne direkte efter hinanden; i tilfælde af en implicit metode resulterer de som løsninger på et ligningssystem. Et typisk eksempel er den eksplicitte, klassiske Runge-Kutta-metoden af orden 4, som undertiden blot kaldes den Runge-Kutta-metoden: Først de fire hjælpestoffer skråninger er brugt ${\ displaystyle k_ {1} = f (t_ {j}, y_ {j})}$${\ displaystyle k_ {2} = f (t_ {j} + h, y_ {j} + hk_ {1})}$${\ displaystyle \ Phi}$${\ displaystyle {\ tfrac {1} {2}} k_ {1} + {\ tfrac {1} {2}} k_ {2}}$${\ displaystyle s}$${\ displaystyle k_ {1}, \ dotsc, k_ {s}}$${\ displaystyle f}$${\ displaystyle \ Phi}$${\ displaystyle k_ {1}, k_ {2}, k_ {3}, \ dotsc}$

${\ displaystyle {\ begin {align} k_ {1} & = f (t_ {j}, y_ {j}) \\ k_ {2} & = f (t_ {j} + {\ tfrac {h} {2 }}, y_ {j} + {\ tfrac {h} {2}} k_ {1}) \\ k_ {3} & = f (t_ {j} + {\ tfrac {h} {2}}, y_ {j} + {\ tfrac {h} {2}} k_ {2}) \\ k_ {4} & = f (t_ {j} + h, y_ {j} + hk_ {3}) \ end {justeret }}}$

og derefter det vægtede gennemsnit som proceshældningen

${\ displaystyle {\ tfrac {1} {6}} k_ {1} + {\ tfrac {1} {3}} k_ {2} + {\ tfrac {1} {3}} k_ {3} + {\ tfrac {1} {6}} k_ {4}}$

Brugt. Denne velkendte metode blev offentliggjort af den tyske matematiker Wilhelm Kutta i 1901, efter at Karl Heun havde fundet en tretrins et-trins metode til ordre 3 et år tidligere .

Konstruktionen af ​​eksplicitte processer af endnu højere orden med det mindst mulige antal trin er et matematisk meget krævende problem. Som John C. Butcher var i stand til at vise i 1965, er der for eksempel kun et minimum af seks-trins procedurer for ordre 5; en eksplicit Runge-Kutta-metode i 8. orden kræver mindst 11 trin. I 1978 fandt den østrigske matematiker Ernst Hairer en procedure af rækkefølge 10 med 17 trin. Koefficienterne for en sådan procedure skal tilfredsstille 1205 bestemmende ligninger. I tilfælde af implicitte Runge-Kutta-metoder er situationen enklere og klarere: for hvert antal trin er der en metode til orden ; dette er samtidig den maksimalt opnåelige ordre.${\ displaystyle s}$${\ displaystyle p = 2s}$

Ekstrapoleringsmetode

Ideen om ekstrapolering er ikke begrænset til at løse initialværdiproblemer med et-trins metoder, men kan anvendes analogt til alle numeriske metoder, der diskretiserer det problem, der skal løses med en trinstørrelse . Et velkendt eksempel på en ekstrapoleringsmetode er Romberg-integrationen til den numeriske beregning af integraler. Lad os generelt være en værdi, der skal bestemmes numerisk, i tilfælde af denne artikel, for eksempel værdien af ​​løsningsfunktionen af ​​et startværdiproblem ved et givet punkt. En numerisk metode, for eksempel en et-trins metode, beregner en omtrentlig værdi for dette , hvilket afhænger af valget af trinstørrelse . Her antages det, at metoden er konvergent, dvs. at mod hvis konvergerer konvergerer til nul. Denne konvergens er dog kun en rent teoretisk erklæring, da man ved reel anvendelse af metoden kan beregne omtrentlige værdier for et endeligt antal forskellige trinstørrelser , men man kan selvfølgelig ikke lade trinstørrelsen "konvergere til nul". De beregnede tilnærmelser for forskellige trinstørrelser kan dog forstås som information om den (ukendte) funktion : I ekstrapolationsmetoden bruges et interpolationspolynom som en tilnærmelse, dvs. et polynom med ${\ displaystyle h}$${\ displaystyle v}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle h> 0}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle v}$${\ displaystyle h}$${\ displaystyle {\ tilde {v}} (h_ {1}), {\ tilde {v}} (h_ {2}), \ dotsc, {\ tilde {v}} (h_ {m})}$${\ displaystyle h_ {1}> h_ {2}> \ ldots> h_ {m}}$${\ displaystyle {\ tilde {v}}}$${\ displaystyle {\ tilde {v}}}$${\ displaystyle P}$

${\ displaystyle P (h_ {k}) = {\ tilde {v}} (h_ {k})}$

til . Værdien af polynomet ved punktet bruges derefter som en beregningsbar tilnærmelse for den ikke-beregne grænse på for mod nul. Roland Bulirsch og Josef Stoer offentliggjorde en tidlig vellykket ekstrapoleringsalgoritme til startværdiproblemer i 1966.${\ displaystyle k = 1,2, \ dotsc, m}$${\ displaystyle P (0)}$${\ displaystyle h = 0}$${\ displaystyle {\ tilde {v}} (h)}$${\ displaystyle h}$

Ekstrapolering i en ordreprocedure${\ displaystyle h = 0}$${\ displaystyle p = 2}$

Et konkret eksempel i tilfælde af en ettrins orden kan gøre den generelle procedure for ekstrapolering forståelig. Med en sådan metode kan den beregnede tilnærmelse for små trinstørrelser let konverteres til et polynom af formen ${\ displaystyle p}$${\ displaystyle h}$

${\ displaystyle P (h) = a + bh ^ {p}}$

med oprindeligt ukendte parametre og omtrentlige. Hvis man nu bruger proceduren til at beregne to tilnærmelser og for en trinstørrelse og for halvdelen af ​​trinstørrelsen , opnår man fra interpolationsbetingelserne og to lineære ligninger for de ukendte og . Den værdi ekstrapoleres til ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h_ {1}}$${\ displaystyle h_ {2} = {\ tfrac {1} {2}} h_ {1}}$${\ displaystyle y_ {h_ {1}}}$${\ displaystyle y_ {h_ {2}}}$${\ displaystyle P (h_ {1}) = y_ {h_ {1}}}$${\ displaystyle P (h_ {2}) = y_ {h_ {2}}}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h = 0}$

${\ displaystyle P (0) = a = y_ {h_ {2}} + {\ frac {y_ {h_ {2}} - y_ {h_ {1}}} {2 ^ {p} -1}}}$

repræsenterer derefter generelt en meget bedre tilnærmelse end de to oprindeligt beregnede værdier. Det kan vises, at rækkefølgen af ​​et-trins-processen opnået på denne måde er mindst , dvs. mindst 1 større end i den oprindelige proces.${\ displaystyle p + 1}$

Fremgangsmåde med trinstørrelseskontrol

En fordel ved et-trins-metoden er, at enhver trinstørrelse kan bruges i hvert trin uafhængigt af de andre trin . I praksis rejser dette naturligvis spørgsmålet om, hvordan man vælger . I virkelige applikationer vil der altid være en fejltolerance, hvormed løsningen på et startværdiproblem skal beregnes; For eksempel ville det være meningsløst at bestemme en numerisk tilnærmelse, der er signifikant "mere præcis" end dataene med målefejl til startværdier og parametre for det givne problem. Målet vil derfor være at vælge trinstørrelser, således at de angivne fejltolerancer på den ene side overholdes, men på den anden side at bruge så få trin som muligt for at holde beregningsindsatsen lille. Generelt kan dette kun opnås, hvis trinstørrelserne er tilpasset løsningens forløb: små trin, hvor løsningen ændres markant, store trin, hvor den næsten er konstant.${\ displaystyle j}$${\ displaystyle h_ {j}}$ ${\ displaystyle h_ {j}}$

I tilfælde af velkonditioneret begyndelsesværdiproblemer, kan det vises, at den globale procedurefejl er omtrent lig med summen af de lokale trunkeringsfejl i de enkelte trin. Derfor bør der vælges en så stor trinstørrelse som muligt, som er under en valgt tolerancetærskel. Problemet her er, at det ikke kan beregnes direkte, da det afhænger af den ukendte nøjagtige løsning af det oprindelige værdiproblem på det tidspunkt . Grundidéen med trinstørrelseskontrol er derfor at tilnærme sig med en metode, der er mere præcis end den grundlæggende metode, den er baseret på.${\ displaystyle \ eta _ {j}: = \ | \ eta (t_ {j}, h_ {j}) \ |}$${\ displaystyle h_ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$${\ displaystyle t_ {j}}$${\ displaystyle y (t_ {j})}$

To grundlæggende ideer til trinstørrelseskontrol halverer trinstørrelsen og de indlejrede procedurer . Ved halvering af trinstørrelsen beregnes resultatet for to trin med halv trinstørrelsen som en sammenligningsværdi ud over det faktiske procestrin. En mere præcis tilnærmelse til bestemmes derefter ud fra begge værdier ved ekstrapolering , og den lokale fejl estimeres således . Hvis dette er for stort, kasseres dette trin og gentages med en mindre trinstørrelse. Hvis den er betydeligt mindre end den angivne tolerance, kan trinstørrelsen øges i det næste trin. Den yderligere beregningsindsats for denne trinstørrelses halveringsmetode er relativt stor; Derfor bruger moderne implementeringer for det meste såkaldte integrerede metoder til kontrol af trinstørrelse. Grundideen er at beregne to tilnærmelser for hvert trin ved hjælp af to et-trinsmetoder, der har forskellige konvergensordrer, og således estimere den lokale fejl. For at optimere computerindsatsen skal de to procedurer have så mange computertrin som muligt til fælles: De skal være "indlejret i hinanden". For eksempel bruger indlejrede Runge-Kutta-metoder de samme ekstra skråninger og adskiller sig kun i, hvordan de gennemsnitliggør dem. Kendte indlejrede metoder inkluderer Runge-Kutta-Fehlberg-metoderne ( Erwin Fehlberg , 1969) og Dormand-Prince-metoderne (JR Dormand og PJ Prince, 1980).${\ displaystyle y (t_ {j})}$${\ displaystyle \ eta _ {j}}$${\ displaystyle y (t_ {j})}$

Praktisk eksempel: Løsning af startværdiproblemer med numerisk software

Talrige softwareimplementeringer er udviklet til de matematiske begreber, der præsenteres i en oversigt i denne artikel, som gør det muligt for brugeren numerisk at løse praktiske problemer på en enkel måde. Som et konkret eksempel skal en løsning af Lotka-Volterra ligningerne beregnes med den meget anvendte numeriske software Matlab . De Lotka-Volterra ligninger er en simpel model fra biologi, der beskriver samspillet mellem rovdyr og byttedyr populationer . Differentialligningssystemet er angivet for dette

${\ displaystyle {\ begin {align} y_ {1} '(t) & = ay_ {1} (t) -by_ {1} (t) y_ {2} (t) \\ y_ {2}' (t ) & = cy_ {1} (t) y_ {2} (t) -dy_ {2} (t) \ end {aligned}}}$

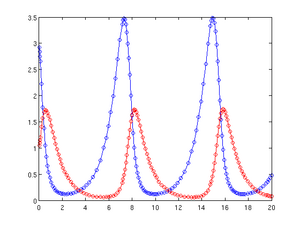
- med parametrene og den oprindelige tilstand - . Her og svarer til den tidsmæssige udvikling af byttet eller rovdyrpopulationen. Løsningen skal beregnes på tidsintervallet . ${\ displaystyle a = 1, b = 2, c = 1, d = 1}$${\ displaystyle y_ {1} (0) = 3}$${\ displaystyle y_ {2} (0) = 1}$${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$${\ displaystyle [0.20]}$

Til beregningen ved hjælp af Matlab defineres først funktionen til højre for differentialligningen for de givne parameterværdier : ${\ displaystyle f}$${\ displaystyle y '= f (t, y)}$

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

Derudover kræves tidsintervallet og de oprindelige værdier:

t_int = [0, 20];
y0 = [3; 1];

Derefter kan løsningen beregnes:

[t, y] = ode45(f, t_int, y0);

Matlab-funktionen ode45implementerer en et-trins metode, der bruger to indlejrede eksplicitte Runge-Kutta-metoder med konvergensordrer 4 og 5 til kontrol af trinstørrelse.

Løsningen kan nu tegnes som en blå kurve og som en rød kurve ; de beregnede punkter er markeret med små cirkler: ${\ displaystyle y_ {1}}$${\ displaystyle y_ {2}}$

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

Resultatet vises nedenfor på billedet til venstre. Det rigtige billede viser de trinstørrelser, der blev brugt af processen og blev genereret med

figure(2)
plot(t(1:end-1), diff(t))

Løsninger af Lotka-Volterra ligningerne

Brugte trin

Dette eksempel kan også udføres med den gratis numeriske software GNU Octave uden ændringer . Med metoden implementeret der er der imidlertid en noget anden trinstørrelsessekvens.

litteratur

• John C. Butcher : Numeriske metoder til almindelige differentialligninger . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 . 
• Wolfgang Dahmen , Arnold Reusken: Numerik til ingeniører og naturforskere . 2. udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , kap. 11: Almindelige differentialligninger . 
• Peter Deuflhard , Folkmar Bornemann : Numerisk matematik 2 - Almindelige differentialligninger . 3. Udgave. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 . 
• David F. Griffiths, Desmond J. Higham: Numeriske metoder til almindelige differentialligninger - indledende værdiproblemer . Springer, London 2010, ISBN 978-0-85729-147-9 . 
• Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , kap. 7: Et-trins procedure til startværdiproblemer . 
• Hans-Jürgen Reinhardt: Numerik af almindelige differentialligninger . 2. udgave. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 . 
• Hans Rudolf Schwarz, Norbert Köckler: Numerisk matematik . 8. udgave. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , kap. 8: Indledende værdiproblemer . 
• Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 . 

Weblinks

• Lars Grüne: Numeriske metoder til almindelige differentialligninger (numerisk matematik II). (PDF) 2008, adgang 20. august 2018 (forelæsningsnotater fra University of Bayreuth ). 
• Peter Spellucci: Numerik af almindelige differentialligninger. (PDF) 2007, adgang 20. august 2018 (forelæsningsnotater fra TU Darmstadt ). 
• Hans U. Fuchs: Numeriske metoder til differentialligninger. (PDF) 2007, adgang den 20. august 2018 (engelsk, forelæsningsnotater fra Zürich Universitet for Anvendte Videnskaber ). 
• Matematik tutorial: første ordens generelle differentialligningsberegner. I: Matematikvejledning. Hentet 20. august 2018 . 

Individuelle beviser

1. ^ Thomas Sonar : 3000 års analyse . Springer, Berlin / Heidelberg 2011, ISBN 978-3-642-17203-8 , pp. 378-388 og 401-426 . 
2. ↑ Jean-Luc Chabert et al.: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 374-378 . 
3. ↑ Wolfgang Dahmen, Arnold Reusken: Numerisk analyse for ingeniører og forskere . 2. udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386 f . 
4. ↑ Wolfgang Dahmen, Arnold Reusken: Numerisk analyse for ingeniører og forskere . 2. udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 386-392 . 
5. ↑ Hans Rudolf Schwarz, Norbert Kockler: Numerisk matematik . 8. udgave. Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1551-4 , pp. 350 f . 
6. ^ Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 157 . 
7. ^ Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 156 . 
8. ^ Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 157 . 
9. ↑ Hans-Jürgen Reinhardt: Numerik af almindelige differentialligninger . 2. udgave. Walter de Gruyter, Berlin / Boston 2012, ISBN 978-3-11-028045-6 , s. 42 f . 
10. ^ John C. Butcher: Numeriske metoder til almindelige differentialligninger . John Wiley & Sons, Chichester 2008, ISBN 978-0-470-72335-7 , pp. 95-100 . 
11. ^ JC Butcher: Numeriske metoder til almindelige differentialligninger i det 20. århundrede . I: Journal of Computational and Applied Mathematics . bånd 125 , nr. 1-2 , 15. december 2000, s. 21 f . ( online ). 
12. De Peter Deuflhard, Folkmar Bornemann: Numerisk matematik 2 - Almindelige differentialligninger . 3. Udgave. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 228 f . 
13. De Peter Deuflhard, Folkmar Bornemann: Numerisk matematik 2 - Almindelige differentialligninger . 3. Udgave. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 229-231 . 
14. ↑ Wolfgang Dahmen, Arnold Reusken: Numerisk analyse for ingeniører og forskere . 2. udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 443 f . 
15. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 258 f . 
16. ↑ Jean-Luc Chabert et al.: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 378 f . 
17. ↑ Jean-Luc Chabert et al.: A History of Algorithms . Springer, Berlin / Heidelberg 1999, ISBN 978-3-540-63369-3 , s. 381-388 . 
18. ↑ Wolfgang Dahmen, Arnold Reusken: Numerisk analyse for ingeniører og forskere . 2. udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-76492-2 , s. 406 f . 
19. ^ JC Butcher: Numeriske metoder til almindelige differentialligninger i det 20. århundrede . I: Journal of Computational and Applied Mathematics . bånd 125 , nr. 1-2 , 15. december 2000, s. 4-6 ( online ). 
20. De Peter Deuflhard, Folkmar Bornemann: Numerisk matematik 2 - Almindelige differentialligninger . 3. Udgave. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 160-162 . 
21. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 219-221 . 
22. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 79 ff . 
23. ^ JC Butcher: Numeriske metoder til almindelige differentialligninger i det 20. århundrede . I: Journal of Computational and Applied Mathematics . bånd 125 , nr. 1-2 , 15. december 2000, s. 26 ( online ). 
24. ^ Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , pp. 171-173 . 
25. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 57-59 . 
26. De Peter Deuflhard, Folkmar Bornemann: Numerisk matematik 2 - Almindelige differentialligninger . 3. Udgave. Walter de Gruyter, Berlin 2008, ISBN 978-3-11-020356-1 , s. 199-204 . 
27. ^ Robert Plato: Numerisk matematik kompakt . 4. udgave. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1018-2 , kap. 7: Et-trins metode til startværdiproblemer , s. 173-177 . 
28. ^ Karl Strehmel, Rüdiger Weiner, Helmut Podhaisky: Numerik af almindelige differentialligninger . 2. udgave. Springer Spectrum, Wiesbaden 2012, ISBN 978-3-8348-1847-8 , s. 64-70 . 
29. ↑ ode45: Løs nonstiff differentialligninger - metode til mellemstor orden. MathWorks, adgang 23. november 2017 .