Brøker

I en snævrere forstand refererer brøkregning til beregning med almindelige brøker (nogle gange også almindelige brøker ) i "tæller-brøk-søjle-nævnerenotation" (se nedenfor). Brøkregning er en del af aritmetik , en gren af matematik .

I en bredere forstand bruges ordet også til beregning med rationelle tal , uanset den måde de skrives på.

En vigtigere forlængelse er optagelse af brøktermer , dette er udtryk, der formelt formes som almindelige brøker, men hvor tælleren og nævneren kan være udtryk, der indeholder variabler . Reglerne for beregning af brøker gælder analogt for disse brøktermer. Beregning med brøktermer er en del af algebra .

Brøkreglerne vedrører de grundlæggende aritmetiske operationer , dvs. addition , subtraktion , multiplikation , division og dannelse af gensidige værdier . Især med brøkdele er der også regler for magter og rødder.

Der er også en reduktions- og ekspansionsregel , som er et særligt træk ved brøker. Det er baseret på forskellen mellem en brøkdel og en brøkdel , som er forklaret mere detaljeret i det følgende afsnit.

Fraktioneret stavning, dvs. stavemåden med en brøkdel, går tilbage til Leonardo von Pisa , der introducerede den i 1228. Det bruges ganske generelt på forskellige områder af matematik, især i algebra , når de elementære regler for brøker, især reduktions- og ekspansionsreglen, finder anvendelse i den struktur, der undersøges. Også her taler man om "brøker", når disse regler anvendes.

Brøk og brøknummer

Beregningen Fraktionen er baseret på det faktum, at det hele (den ene fra beregning med naturlige tal) stadig kan opdeles. For eksempel kan en kage opdeles i fire dele. Hvis disse stykker er af samme størrelse, er hvert stykke en fjerdedel af kagen. Hvis et af kvartererne som på billedet mangler, vises tre fjerdedele kager.

Det hele er opdelt i fire lige store dele; tre af dem er ment her. Eller: tre hele er delt op i fire lige store dele; en af ​​de samme dele er ment.

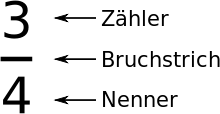
Dette skrives normalt i "tæller-brøk-søjle-nævnerenotation": Tallet under brøklinjen-den såkaldte nævner eller divisor -angiver, hvor mange dele helheden er blevet delt i; nummeret over den del line - den tælleren - angiver, hvor mange dele af det menes i dette tilfælde. Sådan får du en brøkdel . Dette kan også tolkes således: Tælleren angiver, hvor mange hele dele der skal opdeles i lige så mange lige dele som nævneren angiver. (Du lægger tre kager oven på hinanden og deler stakken i fire lige store stakke.)

Hvis det hele (kagen) i stedet er opdelt i otte dele, og seks af dem tages, er det en anden brøkdel: i stedet for . Men disse to fraktioner repræsenterer tilsyneladende den samme mængde kage: de repræsenterer den samme brøkdel . ${\ displaystyle {\ frac {6} {8}}}$${\ displaystyle {\ frac {3} {4}}}$

For hver brøkdel er der mange (uendeligt mange) forskellige repræsentationer , forskellige brøker , som alle repræsenterer den samme værdi (den samme mængde ), men på forskellige måder. Man kan komme fra en fraktion til en anden ved at udvide og forkorte . Dette ændrer ikke værdien af en brøk, men du får forskellige måder at repræsentere dette tal på: forskellige brøker.

Definition og vilkår

Brøker kan i første omgang opdeles i almindelige brøker (også kendt som almindelige brøker ) og decimalfraktioner (= decimaltal, i daglig tale: "punktnummer"), og der er også repræsentationen som en blandet brøk. Når man taler om en brøk, betyder man normalt en almindelig brøk, beregning med decimal brøker kaldes normalt ikke en brøk beregning.

Tabellen nedenfor opsummerer almindelige brøktermer, der er forklaret i dette afsnit. Termerne i nedenstående tabel falder ind under de generiske termer ovenfor, for eksempel er hver pseudofraktion en almindelig brøkdel, tilstødende udtryk behøver ikke at være gensidigt udelukkende. Det skal bemærkes, at dette er betegnelser for nummerskrivninger og ikke for de viste tal. Et bestemt antal kan have forskellige repræsentationer, som hver især er betegnet med forskellige udtryk fra tabellen. For eksempel kan du skrive hver forkert brøk som en blandet brøk.

Andre former, hvor brøker kan vises ( fortsat brøk , procentdel og tusind notation , binære brøker osv.) Behandles i hver separate artikel og er ikke inkluderet i denne tabel.

Almindelige brøker

Beskrivelse af en almindelig brøkdel

Almindelige brøker repræsenteres generelt ved at overlejre tælleren og nævneren adskilt af en vandret linje:

${\ displaystyle {\ frac {Z} {N}}}$

Tæller og nævner for en brøkdel er hele tal . Nævneren må ikke være nul, fordi division med nul ikke er defineret. ${\ displaystyle N}$

Hver fraktion kan også forstås som et delingsproblem . Tælleren er det udbytte , nævneren er den divisor: ${\ displaystyle Z}$${\ displaystyle N}$

${\ displaystyle Z: N = {\ frac {Z} {N}}}$

Den afgørende faktor i brøker er, at hver division (undtagen med nul) er mulig og har et resultat, der let kan repræsenteres, mens reglerne for delbarhed gælder for hele tal .

Normalt bruges naturlige tal til tælleren og nævneren, og ethvert negativt tegn placeres foran brøken, for eksempel i stedet for eller . Hvis tælleren og nævneren er negativ, betegner dette den positive brøk i henhold til reglerne for dividering af hele tal :${\ displaystyle - {\ tfrac {3} {4}}}$${\ displaystyle {\ tfrac {-3} {4}}}$${\ displaystyle {\ tfrac {3} {- 4}}}$${\ displaystyle {\ tfrac {-3} {- 4}} = {\ tfrac {3} {4}}}$

I en variant af denne notation, som ofte bruges, når almindelige brøker forekommer i tekster, skrives tælleren, brøklinjen og nævneren efter hinanden, og der bruges en skråstreg som brøklinjen , for eksempel 1/2, 3/8 . I notationslinjen i stedet for den vandrette brøkstang er (især) ciffer tæller og nævner undertiden reduceret over eller skrevet under skråstregen: ⁶ / ₇ . Til dette formål findes specialtegn som ¾ eller ½ i mange udskrivningstegnsæt.

Ægte og falske brøker

Hvis der på en brøkdel af mængden af tælleren er mindre end nævneren, så taler man om en reel eller faktiske fraktur (z. B. eller ), ellers fra en falsk eller forkert fraktion (z. B. eller ). ${\ displaystyle {\ tfrac {6} {7}}}$${\ displaystyle {\ tfrac {2} {5}}}$${\ displaystyle {\ tfrac {7} {7}}}$${\ displaystyle {\ tfrac {11} {3}}}$

Så reelle brøker er dem, hvis mængde er mindre end en helhed.

Bagagerumsbrud og grenbrud

Hvis tælleren i en almindelig brøk er 1 (f.eks. Eller ), taler vi om en stamfraktion , ellers er det en afledt brøk eller grenfraktion . ${\ displaystyle {\ tfrac {1} {2}}}$${\ displaystyle {\ tfrac {1} {9}}}$

Pseudo går i stykker

Forkerte brøker, hvor tælleren er et heltal af nævneren (f.eks. ), Kaldes dummyfraktioner, fordi de kan konverteres til hele tal ved at forkorte dem (i eksemplet til tallet 4). Især kan hvert helt tal skrives som en dummy -brøk . ${\ displaystyle {\ tfrac {12} {3}}}$${\ displaystyle n}$${\ displaystyle {\ tfrac {n} {1}}}$

Blandede fraktioner

Forkerte brøker, der ikke er pseudo-fraktioner, kan altid repræsenteres som blandede brøker (også: som blandede tal, i blandet notation).

Først og fremmest hele taldelen, dvs. H. tallet rundede til nul, skrevet og derefter umiddelbart efter den resterende del som en reel brøkdel. For eksempel i stedet for eller i stedet for . ${\ displaystyle 1 {\ tfrac {1} {3}}}$${\ displaystyle {\ tfrac {4} {3}}}$${\ displaystyle -3 {\ tfrac {3} {5}}}$${\ displaystyle - {\ tfrac {18} {5}}}$

Et problem med blandet stavemåde er, at det kan misforstås som et produkt:

Så står mest for og ikke for . ${\ displaystyle 2 {\ tfrac {1} {3}}}$${\ displaystyle 2 + {\ tfrac {1} {3}} = {\ tfrac {7} {3}}}$${\ displaystyle 2 \ cdot {\ tfrac {1} {3}} = {\ tfrac {2} {3}}}$

Hvis du skriver på den anden side , er det ikke en brøkdel i blandet notation, men (på grund af variablerne) et udtryk . Her skal det udeladte aritmetiske symbol være et malerpunkt (andre aritmetiske symboler må ikke udelades i termer). skal derfor forstås som og aldrig som . ${\ displaystyle a {\ tfrac {b} {c}}}$${\ displaystyle a {\ tfrac {b} {c}}}$${\ displaystyle a \ cdot {\ tfrac {b} {c}}}$${\ displaystyle a + {\ tfrac {b} {c}}}$

Beregningsregler

Praktisk regning med brøker

Ved beregning med brøker i de fire grundlæggende aritmetiske operationer for addition , subtraktion , multiplikation og division , er to brøker knyttet til at oprette et tredje tal. Dette skal ikke forveksles med omformning af brøker, hvor en enkelt brøkdel får en ny form uden at ændre dens værdi.

Den danner (ændringen i formen) ofte en forudsætning for frakturer kan forventes. Derfor behandles det her først.

Ændring i form af brud

Konverter til et decimaltal

Hvis du vil konvertere en brøk til et decimalpunkt, skal du blot dividere tælleren med nævneren. giver 0,75 eller 75% af det hele. ${\ displaystyle {\ tfrac {3} {4}}}$

Udvid og afkort

Brøkværdien repræsenteret af en brøk ændres ikke, hvis du gange tælleren og nævneren for brøken med det samme tal (ikke lig med 0) ( udvid brøken ) eller dividerer brøken med en fælles divisor for tæller og nævner ( forkort fraktionen ).

Eksempel: . Læst fra venstre mod højre er brøkdelen blevet udvidet, og fra højre til venstre er den blevet forkortet. ${\ displaystyle {\ tfrac {2} {3}} = {\ tfrac {2 \ cdot 3} {3 \ cdot 3}} = {\ tfrac {6} {9}}}$

Indstil blandede tal, og del hele

Værdien af ​​en brøkdel, der vises i blandet notation, ændres ikke, hvis heltalsdelen skrives som en dummy -brøk med nævneren af ​​fraktionen, og de resterende brøker tilføjes. Omvendt, i tilfælde af en ukorrekt brøkdel, kan du opdele fraktionerne, der udgør helheden, og tilføje de resterende brøker.

Eksempel: . Hele numre blev delt fra venstre til højre, og blandede tal blev oprettet fra højre til venstre. ${\ displaystyle {\ tfrac {8} {3}} = {\ tfrac {6} {3}} + {\ tfrac {2} {3}} = 2 + {\ tfrac {2} {3}} = 2 {\ tfrac {2} {3}}}$

Lav brøker med samme navn

Almindelige brøker, der har samme nævner, kaldes de samme . Hvis brøker udvides på en sådan måde, at de derefter har samme nævner, kaldes dette at lave det samme navn . I praktisk aritmetik, den vigtigste nævner for bør bestemmes fraktionerne, er dette den laveste fælles multiplum (lcm) i nævneren.

Eksempel: Fraktionerne skal laves med samme navn. LCM er nævneren , så alle tre fraktioner udvides, så deres nævner er 42: ${\ displaystyle {\ tfrac {2} {7}}; {\ tfrac {1} {6}}; {\ tfrac {9} {14}}}$${\ displaystyle 2 \ times 3 \ times 7 = 42}$

${\ displaystyle {\ tfrac {2} {7}} = {\ tfrac {2 \ cdot 6} {42}} = {\ tfrac {12} {42}}; \ quad {\ tfrac {1} {6} } = {\ tfrac {1 \ cdot 7} {42}} = {\ tfrac {7} {42}}; \ quad {\ tfrac {9} {14}} = {\ tfrac {9 \ cdot 3} { 42}} = {\ tfrac {27} {42}}}$.

Repræsentationerne med samme navn kan nu f.eks. Bruges til at bestille de viste fraktioner efter størrelse ved at sammenligne deres tællere:

${\ displaystyle {\ tfrac {7} {42}} <{\ tfrac {12} {42}} <{\ tfrac {27} {42}} \; \;}$, så skal gælde.${\ displaystyle \; \; {\ tfrac {1} {6}} <{\ tfrac {2} {7}} <{\ tfrac {9} {14}} \;}$

Grundregning

Tilføj og træk fra

Eksempel på tilføjelse af to almindelige brøker med samme navn. Den ene lyder: " tre fjerdedele plus en fjerdedel "${\ displaystyle {\ tfrac {3} {4}} + {\ tfrac {1} {4}} = 1}$

De fraktioner, der skal tilføjes eller trækkes fra, får først samme navn, derefter tilføjes eller trækkes deres tællere.

Eksempel: . ${\ displaystyle {\ tfrac {1} {6}} + {\ tfrac {2} {15}} = {\ tfrac {5} {30}} + {\ tfrac {4} {30}} = {\ tfrac {9} {30}} = {\ tfrac {3} {10}}}$

Formere sig

Brøker ganges ved at gange deres tællere og nævnere sammen. Tællerens produkt er derefter tælleren af ​​resultatet, nævneren er derefter nævneren af ​​resultatet.

Eksempel: . ${\ displaystyle {\ tfrac {2} {3}} \ cdot {\ tfrac {9} {14}} = {\ tfrac {2 \ cdot 9} {3 \ cdot 14}} = {\ tfrac {3} { 7}}}$

At dele

En brøkdel divideres med at multiplicere med dens gensidige .

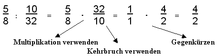
Eksempel: . ${\ displaystyle {\ tfrac {2} {15}}: {\ tfrac {14} {27}} = {\ tfrac {2} {15}} \ cdot {\ tfrac {27} {14}} = {\ tfrac {2} {3 \ cdot 5}} \ cdot {\ tfrac {3 \ cdot 9} {2 \ cdot 7}} = {\ tfrac {1 \ cdot 9} {5 \ cdot 7}} = {\ tfrac {9} {35}}}$

Som vist i eksemplet kan mellemresultaterne forkortes (her f.eks. 3 og 2 i det næstsidste trin).

Gør matematik med blandede brøker

Når man multiplicerer eller deler blandede fraktioner, er det normalt nødvendigt først at konvertere dem til almindelige brøker. (Bortset fra meget enkle opgaver, f.eks .) ${\ displaystyle 6 {\ tfrac {1} {3}}: 2 = 3 {\ tfrac {1} {6}}}$

Når man tilføjer og fratrækker, er det på den anden side meget billigere at se det hele isoleret og kun bruge brøker til de resterende reelle brøker. Ved tilføjelse kan der vises en ekstra helhed her, når fraktionerne måske ikke er tilstrækkelige, så en af ​​helheden skal opdeles for at danne en tilsyneladende brøk:

${\ displaystyle 13 {\ tfrac {3} {4}} + 27 {\ tfrac {1} {2}} = 40+ \ venstre ({\ tfrac {3} {4}} + {\ tfrac {1} { 2}} \ højre) = 40 + 1 {\ tfrac {1} {4}} = 41 {\ tfrac {1} {4}}}$;

${\ displaystyle 16 {\ tfrac {1} {3}} - 9 {\ tfrac {1} {2}} = 7+ \ venstre ({\ tfrac {1} {3}} - {\ tfrac {1} { 2}} \ højre) = 7 + \ venstre ({\ tfrac {2} {6}} - {\ tfrac {3} {6}} \ højre) = 6 + \ venstre ({\ tfrac {6} {6 }} + {\ tfrac {2} {6}} - {\ tfrac {3} {6}} \ right) = 6 {\ tfrac {5} {6}}}$.

Abstrakte beregningsregler

Følgende regler gælder for både brøker i snævrere forstand og ved beregning med brøktermer. Ved beregning med brøker repræsenterer variablerne i reglerne visse hele tal. Hvis du i stedet bruger andre udtryk til disse variabler, f.eks. Hvis du f.eks. Selv indtaster reelle brøker, decimalbrøker eller termer, får du regler til beregning med brøktermer, brøker i bredere forstand. ${\ displaystyle a, \; b, \; c, \; d, \; n \;}$

Ved beregning med brøker giver de abstrakte beregningsregler altid korrekte resultater, og beregningen ved hjælp af "praktiske beregningsregler" er ofte mindre tidskrævende.

Udvid og afkort

Forkort ${\ displaystyle \ rightarrow}$
${\ displaystyle {\ frac {a \ cdot c} {b \ cdot c}} = {\ frac {a} {b}}}$
${\ displaystyle \ leftarrow}$ Udvide

Nyttige æselbroer er:

• Skær faktorer, det er godt; den, der skærer beløb, er et får.
• Forskelle og summer skærer kun de dumme.
• Hvad du gør ovenfor, gør du herunder!

Af ækvivalensen for alle naturlige tal følger det, at hvert rationelt tal kan repræsenteres med et uendeligt antal forskellige brøker, fordi det holder . ${\ displaystyle {\ frac {a} {b}} = {\ frac {a \ cdot c} {b \ cdot c}}}$${\ displaystyle c> 0}$${\ displaystyle {\ frac {a} {b}} = {\ frac {2a} {2b}} = {\ frac {3a} {3b}} = {\ frac {4a} {4b}} = \ dotsb}$

tilføjelse

${\ displaystyle {\ frac {a} {b}} \; + \; {\ frac {c} {d}} \; = \; {\ frac {a \ cdot d + c \ cdot b} {b \ cdot d}}}$

subtraktion

${\ displaystyle {\ frac {a} {b}} - {\ frac {c} {d}} \; = \; {\ frac {a \ cdot dc \ cdot b} {b \ cdot d}}}$

multiplikation

${\ displaystyle {\ frac {a} {b}} \; \ cdot \; {\ frac {c} {d}} \; = \; {\ frac {a \ cdot c} {b \ cdot d}} }$

${\ displaystyle {\ frac {a} {b}} \; \ cdot \; n \; = \; {\ frac {a \ cdot n} {b}}}$

division

Eksempel på division med en brøkdel

${\ displaystyle {\ frac {a} {b}}: {\ frac {c} {d}} \; = \; {\ frac {a} {b}} \; \ cdot \; {\ frac {d } {c}} \; = \; {\ frac {a \ cdot d} {b \ cdot c}}}$

Så du deler med en brøk ved at multiplicere med brøkens reciprokke , som fungerer som en divisor . Divisionen reduceres derfor til multiplikationen.

${\ displaystyle {\ frac {a} {b}}: n \; = \; {\ frac {a} {b \ cdot n}} \ quad {\ text {og}} \ quad n: {\ frac { a} {b}} \; = \; {\ frac {n \ cdot b} {a}}}$

Potenser

Herske	eksempel
${\ displaystyle {\ frac {a ^ {n}} {b ^ {m}}} = a ^ {n} \ cdot b ^ {- m}}$	${\ displaystyle {\ frac {3} {2}} = 3 \ cdot 2 ^ {- 1}}$
${\ displaystyle {\ frac {a ^ {n}} {a ^ {m}}} = a ^ {nm}}$	${\ displaystyle {\ frac {a ^ {3}} {a ^ {2}}} = a ^ {3} \ cdot a ^ {- 2} = a ^ {3-2} = a}$
${\ displaystyle {\ frac {a ^ {n}} {b ^ {n}}} = \ venstre ({\ frac {a} {b}} \ højre) ^ {n}}$	${\ displaystyle {\ frac {3 ^ {2}} {2 ^ {2}}} = \ venstre ({\ frac {3} {2}} \ højre) ^ {2}}$

Beregning med brøkdele

Brøkdele, dvs. aritmetiske udtryk i form af almindelige brøker, spiller en vigtig rolle i elementær algebra. Generelt indeholder fraktion Terme også tal næste variabler . Beregningsreglerne for brøker kan også anvendes på brøktermer.

Definitionsdomæne

Ved bestemmelse af definitionsområdet for en brøkterm, skal det bemærkes, at nævneren ikke må have værdien 0. For eksempel ville fraktionsudtrykket, der afhænger af , ikke blive defineret, når der indsættes . Domænet er derfor, hvis mængden af reelle tal antages som grundsæt . I mere komplicerede tilfælde bør nævneren opdeles i faktorer, så definitionsområdet kan identificeres. ${\ displaystyle x}$${\ displaystyle {\ tfrac {1} {6-2x}}}$${\ displaystyle x = 3}$${\ displaystyle D = \ mathbb {R} \ setminus \ {3 \}}$

Eksempel: har definitionens domæne . ${\ displaystyle {\ tfrac {x} {x ^ {2} -9}} = {\ tfrac {x} {(x + 3) (x -3)}}}}$${\ displaystyle D = \ mathbb {R} \ setminus \ {- 3; +3 \}}$

Forkort

At forkorte betyder, at du deler tælleren og nævneren med det samme aritmetiske udtryk. Det er vigtigt, at kun produktfaktorer kan fjernes. Summer og forskelle i tæller og nævner skal muligvis først opdeles i produkter ( faktorisering ).

Eksempler:

1. ${\ displaystyle \ quad {\ frac {4abc ^ {3}} {6a ^ {2} bc}} = {\ frac {2c ^ {2}} {3a}}}$
2. ${\ displaystyle \ quad {\ frac {x ^ {2} -6xy + 9y ^ {2}} {2x-6y}} = {\ frac {(x-3y) ^ {2}} {2 (x-3y )}} = {\ frac {x-3y} {2}}}$

Ved afkortning af en brøkperiode kan definitionsområdet ændre sig! I det første eksempel er det ikke -forkortede udtryk til venstre kun defineret, hvis det gælder, det til højre er allerede defineret, hvis det kun gælder. I det andet eksempel defineres det ikke -forkortede udtryk kun, hvis det forkortede udtryk er defineret uden begrænsninger. ${\ displaystyle a, b, c \ neq 0}$${\ displaystyle a \ neq 0}$${\ displaystyle x \ neq 3y}$

Ændring af definitionsintervallet for en brøkterm ved afkortning er en af ​​de teknikker, hvormed funktionsbetingelser kan fortsættes kontinuerligt .

Addition og subtraktion

Som med tal er det nødvendigt at give de givne brøkbetegnelser det samme navn, dvs. H. at bringe til samme nævner. Den enkleste mulige fællesnævner (hovednævner) bestemmes, som er delelig med alle givne nævnere.

Eksempel:

${\ displaystyle {\ frac {3} {2a ^ {2}}} - {\ frac {4ab -1} {2ab}} + 2}$

Hovednævneren er . Ekspansionsfaktorerne for de tre givne brøktermer opnås ved at dividere hovednævner fundet med den tidligere nævner. Så ekspansionsfaktorerne er , og . ${\ displaystyle 2a ^ {2} b}$${\ displaystyle b}$${\ displaystyle a}$${\ displaystyle 2a ^ {2} b}$

${\ displaystyle {\ frac {3} {2a ^ {2}}} - {\ frac {4ab -1} {2ab}} + 2}$

${\ displaystyle = {\ frac {3 \ gange b- (4ab-1) \ gange a + 2 \ gange 2a ^ {2} b} {2a ^ {2} b}}}$

${\ displaystyle = {\ frac {3b-4a ^ {2} b + a + 4a ^ {2} b} {2a ^ {2} b}} = {\ frac {3b + a} {2a ^ {2} b}}}$

Ofte kan hovednævneren kun identificeres, hvis nævnerne er opdelt i faktorer (faktorisering). Metoden til factoring bruges ofte eller binomiske formler bruges .

Eksempel:

${\ displaystyle {\ frac {x} {x ^ {2} -xy}} - {\ frac {y} {x ^ {2} + xy}} - {\ frac {x} {x ^ {2} - y ^ {2}}}}$

${\ displaystyle = {\ frac {x} {x (xy)}} - {\ frac {y} {x (x + y)}} - {\ frac {x} {(x + y) (xy)} }}$

${\ displaystyle = {\ frac {x \ cdot (x + y) -y \ cdot (xy) -x \ cdot x} {x (x + y) (xy)}}}}$

${\ displaystyle = {\ frac {x ^ {2} + xy -xy + y ^ {2} -x ^ {2}} {x (x + y) (xy)}} = {\ frac {y ^ { 2}} {x (x + y) (xy)}}}$

Multiplikation og division

Ved multiplikation af brøkdele skal både tællere og nævnere multipliceres. Faktorer, der er fælles for tælleren og nævneren, skal afkortes.

Eksempel: ${\ displaystyle {\ frac {4xy} {z ^ {2}}} \ cdot {\ frac {xz} {6y}} = {\ frac {4x ^ {2} yz} {6yz ^ {2}}} = {\ frac {2x ^ {2}} {3z}}}$

Ved mere komplicerede opgaver bør tæller og nævner opdeles i faktorer for at kunne fjerne dem før den faktiske multiplikation.

Eksempel: ${\ displaystyle {\ frac {a -2b} {4a + 1}} \ cdot {\ frac {16a ^ {2} -1} {a ^ {2} -4ab + 4b ^ {2}}} = {\ frac {a-2b} {4a + 1}} \ cdot {\ frac {(4a + 1) (4a-1)} {(a-2b) ^ {2}}} = {\ frac {4a-1} {a-2b}}}$

Opdelingen af ​​brøktermer kan reduceres til multiplikation. Du deler med en brøkdel ved at gange med dens gensidige .

Eksempel: ${\ displaystyle {\ frac {2x-3} {5x}}: {\ frac {4x ^ {2} -9} {10x ^ {2}}} = {\ frac {2x-3} {5x}} \ cdot {\ frac {10x ^ {2}} {(2x + 3) (2x-3)}} = {\ frac {2x} {2x + 3}}}$

Andre former for repræsentation

Delvise fraktioner

Brøker kan ofte opdeles i såkaldte delfraktioner , hvis nævnere er hele kræfter for primtal ; z. B.:

${\ displaystyle {\ frac {5} {6}} = {\ frac {1} {2}} + {\ frac {1} {3}},}$

${\ displaystyle {\ frac {1} {6}} = {\ frac {1} {2}} - {\ frac {1} {3}}, \,}$

${\ displaystyle {\ frac {1} {72}} = {\ frac {1} {8}} - {\ frac {1} {9}},}$

${\ displaystyle {\ frac {1} {60}} = {\ frac {-1} {4}} - {\ frac {4} {3}} + {\ frac {8} {5}}.}$

Egyptiske brøker

Der er også nedbrydninger som såkaldte egyptiske fraktioner ( stamfraktioner ), f.eks. B.

${\ displaystyle {\ frac {3} {7}} = {\ frac {1} {3}} + {\ frac {1} {11}} + {\ frac {1} {231}}}$ og

${\ displaystyle {\ frac {25} {31}} = {\ frac {1} {2}} + {\ frac {1} {4}} + {\ frac {1} {18}} + {\ frac {1} {1116}}}$,

de gamle egyptere kendte og beregnede kun sådanne summer.

Pythagoranske fraktioner

Tallet triple er et eksempel på en pythagoreansk brøkdel (se også Pythagoras triple ), fordi ${\ displaystyle ({\ tfrac {1} {5}}, {\ tfrac {24} {35}}, {\ tfrac {5} {7}})}$

${\ displaystyle \ left ({\ frac {1} {5}} \ right) ^ {2} + \ left ({\ frac {24} {35}} \ right) ^ {2} = \ left ({\ frac {5} {7}} \ højre) ^ {2}}$.

Rationel tæller eller nævner

Se rationalisering (fraktioner) .

Generaliseringer

Konstruktionen af feltet med rationelle tal som brøker fra ringen med hele tal generaliseres i abstrakt algebra ved begrebet kvotfeltet til eventuelle integritetsringe .

Se også

• Farey episode
• Korsmultiplikation

litteratur

• Erhard Cramer, Johanna Nešlehová: forkursus i matematik . Arbejdsbog til studiestart på bacheloruddannelser. 3., verb. Udgave. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-78180-6 , s. 77-83 . 
• Friedhelm Padberg: Almindelige brøker - decimalfraktioner. Fraktionsberegningsdidaktik . BI-Wissenschafts-Verlag, 1989, ISBN 3-411-03207-3 . 

Weblinks

Wikibooks: Matematik til skole${\ displaystyle {\ color {BlueViolet} {\ begin {matrix} {\ mathbf {MATHE} \ mu \ alpha T \ mathbb {R} ix} \ end {matrix}}}}}$  - grundlæggende aritmetiske og fraktionelle beregninger

Wikibooks: Matematik til skole${\ displaystyle {\ color {BlueViolet} {\ begin {matrix} {\ mathbf {MATHE} \ mu \ alpha T \ mathbb {R} ix} \ end {matrix}}}}}$  - brøkdele

Wiktionary: Fraktionsberegning  - forklaringer på betydninger, ordoprindelse, synonymer, oversættelser

• Brøkregning illustreret i undervisningsvideoer (Olaf Hinrichsen, OberPrima.com UG, 16. marts 2018)
• Fraktionsberegner - forskellige online programmer til brøker
• Formler til beregning af brøker - En klar liste over de vigtigste formler til beregning med brøker
• Interaktiv applet, der guider dig gennem de forskellige opgaver til at beregne brøker

Individuelle beviser

1. ↑ H. Wussing: Foredrag om matematikkens historie . VEB Deutscher Verlag der Wissenschaften, 1979, s. 325
2. ↑ Officielle stavebestemmelser af 1. august 2006, §106, Canoonet