Projektion (lineær algebra)

Den lineære kortlægning T er projektionen langs k på m. Alle punkter i billedet m (f.eks. W ) kortlægges af T på sig selv (f.eks. Tw ).

I matematik er en projektion eller projektor en særlig lineær kortlægning ( endomorfisme ) over et vektorrum, der efterlader alle vektorer i dets billede (et underrum af ) uændret. ${\ displaystyle V}$${\ displaystyle V}$

Hvis en base af vælges korrekt , indstiller projektionen nogle komponenter i en vektor til nul og holder de andre. Dette retfærdiggør klart udtrykket projektion, såsom illustrationen af ​​et hus i en to-dimensionel grundplan. ${\ displaystyle V}$

definition

Lad være et vektorrum . En vektorrumsendomorfisme kaldes en projektion, hvis den er idempotent , dvs. hvis den holder. ${\ displaystyle V}$ ${\ displaystyle P \ kolon V \ til V}$${\ displaystyle P \ circ P = P}$

egenskaber

En projektion kan kun have tallene 0 og 1 som egenværdier . Ejrummet er

• ${\ displaystyle \ ker P}$( Core of ) til egenværdien 0 og${\ displaystyle P}$
• ${\ displaystyle \ operatorname {im} P}$( Billede fra ) til egenværdien 1.${\ displaystyle P}$

Det samlede rum er den direkte sum af disse to underrum :

${\ displaystyle V = \ ker P \ oplus \ operatorname {im} P}$

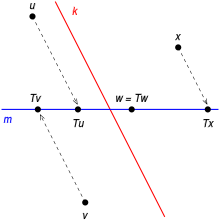
Illustrationen viser tydeligt en parallel projektion langs . ${\ displaystyle P}$${\ displaystyle \ operatorname {im} P}$${\ displaystyle \ ker P}$

Hvis der er en projektion, er der også en projektion, og følgende gælder: ${\ displaystyle P}$${\ displaystyle \ operatorname {id} -P}$

${\ displaystyle \ ker P = \ operatorname {im} (\ operatorname {id} -P)}$

${\ displaystyle \ operatorname {im} P = \ ker (\ operatorname {id} -P)}$

Fremskrivninger og komplement

Hvis der er et vektorrum og et underområde, så er der generelt mange fremskrivninger på , dvs. projektioner, hvis billede er. Hvis der er en projektion med et billede , så er der et supplement til in . ${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle P}$${\ displaystyle U}$${\ displaystyle \ ker P}$${\ displaystyle U}$${\ displaystyle V}$

Omvendt, hvis et supplement af in , så , så kan hver som en sum med klart specificeret og repræsentere. Endomorfismen af , som tildeler hvad der hører til hver , er en projektion med et billede og en kerne . Fremskrivninger og nedbrydninger i komplementære underområder svarer til hinanden. ${\ displaystyle W}$${\ displaystyle U}$${\ displaystyle V}$${\ displaystyle V = U \ oplus W}$${\ displaystyle v \ in V}$${\ displaystyle v = u + w}$${\ displaystyle u \ i U}$${\ displaystyle w \ in W}$${\ displaystyle V}$${\ displaystyle v}$${\ displaystyle u}$${\ displaystyle U}$${\ displaystyle W}$

Vinkelret projektion

Ortogonal nedbrydning af en vektor i en del i et plan og en del i det ortogonale komplement af planet${\ displaystyle v}$${\ displaystyle P (v) = u}$${\ displaystyle U}$${\ displaystyle vP (v) = u ^ {\ perp}}$${\ displaystyle U ^ {\ perp}}$

Hvis et endeligt dimensionelt reelt eller komplekst vektorrum med et skalarprodukt , er der en projektion langs det ortogonale komplement for hvert subvektorrum , der kaldes "ortogonal projektion på ". Det er den entydigt bestemte lineære kortlægning med egenskaben, der for alle${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle U}$${\ displaystyle P \ kolon V \ til V}$${\ displaystyle v \ in V}$

• ${\ displaystyle P (v) \ i U}$ og
• ${\ displaystyle vP (v) \ perp U}$

gælder.

Hvis der er et uendeligt dimensionelt Hilbert-rum , gælder denne erklæring med projektionssætningen i overensstemmelse hermed for lukkede undervektorrum . I dette tilfælde kan kontinuerlig vælges. ${\ displaystyle V}$${\ displaystyle U}$${\ displaystyle P}$

Eksempler

Som enkle eksempler kan for hvert vektorrum identiteten og figuren for tilstand som trivielle fremskrivninger (som kan repræsenteres af enhed eller nul matrix). ${\ displaystyle V}$${\ displaystyle Id: v \ mapsto v}$${\ displaystyle N \ colon v \ mapsto 0}$${\ displaystyle v \ in V}$

Lad det være kortlægningen af ​​flyet i sig selv, der føres gennem matrixen ${\ displaystyle P}$${\ displaystyle \ mathbb {R} ^ {2}}$

${\ displaystyle P = {\ begin {pmatrix} 1 & 0 \\ 0 & 0 \ end {pmatrix}}}$

er beskrevet. Den projicerer en vektor på , dvs. ortogonalt på x-aksen. Egenrummet for egenværdi , dvs. kernen, er spændt af , egenrummet for egenværdi , dvs. billedet, er spændt af. Projektoren er den vinkelrette projektion på y-aksen. ${\ displaystyle {\ tbinom {x} {y}}}$${\ displaystyle {\ tbinom {x} {0}}}$${\ displaystyle 0}$${\ displaystyle {\ tbinom {0} {1}}}$${\ displaystyle 1}$${\ displaystyle {\ tbinom {1} {0}}}$${\ displaystyle \ operatorname {id} -P}$

I modsætning hertil er for eksempel gennem matrixen

${\ displaystyle P = {\ begin {pmatrix} 1 & -1 \\ 0 & 0 \ end {pmatrix}}}$

Det beskrevne billede af planet skyldes også en projektion, men ikke en ortogonal projektion. Dens billede er igen x-aksen, men dens kerne er den lige linje med ligningen . ${\ displaystyle P ^ {2} = P}$${\ displaystyle y = x}$

Ansøgning

I kvantemekanik taler man i forbindelse med måleprocessen om en projektion af tilstandsvektoren ψ, hvor den nøjagtige fortolkning er beskrevet nedenfor:

• Som måleresultat kommer kun en af ​​i. A. sætter spørgsmålstegn ved et uendeligt antal såkaldte egenværdier af de observerede observerbare (dvs. den tildelte selvtilhørende operatør i systemets tilstandsrum, det såkaldte Hilbert-rum ). Valget foretages tilfældigt ( Københavns fortolkning ) med en vis sandsynlighed, som ikke kræves her.
• Beregningen af ​​sandsynligheden for en egenværdi (måleresultat) finder blandt andet sted ved hjælp af projektionen på dens egenrum .

Totaliteten af projiceringsoperatørerne opnået på denne måde er "komplet" for en given målt variabel og resulterer i den såkaldte spektrale repræsentation af de observerbare.

svulme

• Gerd Fischer : Lineær algebra. Vieweg-Verlag, ISBN 3-528-03217-0 .
• Dirk Werner : Funktionsanalyse. 6., korrigeret udgave, Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6 , side 161.