Partikelstørrelsesfordeling

Udtrykket partikelstørrelsesfordeling er lånt fra statistikker . Der er frekvenser og frekvensfordelinger af enhver funktion, f.eks. B. terningøjne, fremstillingstolerancer osv. Overvejet. Inden for partikelteknologi og partikelmålingsteknologi eller dispersitetsanalyse vælges den ækvivalente diameter af en partikel som et træk . Partikelstørrelsesfordelingen skyldes således den generelle frekvensfordeling af statistikkerne. Dette er ofte omtalt som den kornstørrelse fordeling .

Definitioner

Partiklerne (spredes fase) i et omgivende medium (kontinuerlig fase), dvs. H. Korn, dråber eller bobler differentieres ved hjælp af en ækvivalent diameter, der skal måles og klassificeres i udvalgte klasser efter deres størrelse. For at repræsentere en partikelstørrelsesfordeling bestemmes de forhold, hvormed de respektive partikelklasser er involveret i dispergeringsfasen.

Der anvendes forskellige typer mængder . Hvis partiklerne tælles, er antallet af størrelse antallet. I tilfælde af vejning er det imidlertid massen eller, i tilfælde af homogen densitet ρ, volumen. Andre stammer fra længder, fremspring og overflader. Man skelner mellem:

Mængde type	Indeks r	Målemetode (eksempler)
nummer	0	elektrisk mobilitetsanalyse
længde	1	Sedimentationsanalyse
areal	2	Absorbansmåling
Volumen (masse)	3	Sigteanalyse

Der anvendes et standardiseret kvantitetsmål til den grafiske repræsentation. Normaliseringen er nødvendig for at eliminere proportionernes afhængighed af den samlede anvendte mængde. På denne måde kan resultatet af en første vejning på 100 g total masse sammenlignes med resultatet af en vejning på 1 kg total masse.

Der skelnes mellem to størrelser:

• Kumulativ fordeling Q _r
• Tæthedsfordeling q _r

Udtrykkene Q _r og q _r er symboler på udtrykket fraktil . Indekset r angiver typen af ​​mængde i henhold til tabellen ovenfor.

Generelt når grafer en partikelstørrelsesfordeling, den ækvivalente diameter er x afbildet på abscissen og mængden Q _r eller q _r på ordinaten .

Kumulativ fordelingskurve

Den kumulative fordelingskurve Q _r (x) angiver den standardiserede mængde af alle partikler med en ækvivalent diameter på mindre end eller lig med x . De kumulative fordelinger af de to mest almindelige typer af størrelser defineres eksplicit nedenfor:

• Partikelnummer ( r = 0 )

Lad N _{i være} antallet af alle undersøgte partikler med en diameter x mindre end eller lig med den undersøgte diameter x _i og N det samlede antal af alle undersøgte partikler. Derefter

${\ displaystyle Q_ {0} (x_ {i}) = {\ frac {N_ {i}} {N}}}$

• Partikelmasse ( r = 3 )

Lad m _{i være} massen af ​​alle undersøgte partikler med en diameter x mindre end eller lig med den betragtede diameter x _i og m den samlede masse af alle undersøgte partikler. Derefter

${\ displaystyle Q_ {3} (x_ {i}) = {\ frac {m_ {i}} {m}}}$

Den samme procedure anvendes til de andre typer mængder.

På grund af normaliseringen, i. H. den respektive opdeling med det samlede beløb gælder

• ${\ displaystyle Q_ {r} (x = 0) = Q_ {r} (x = x _ {\ mathrm {min}}) = 0}$
• ${\ displaystyle Q_ {r} (x = \ infty) = Q_ {r} (x = x _ {\ mathrm {max}}) = 1}$

Mængden Q _r er altid dimensionsløst.

Følgende diagram viser en typisk kumulativ fordelingskurve med den mindste og maksimale ækvivalente diameter x _min og x _max . De diskrete elementer i den kumulative fordeling er afbildet mod de individuelle øvre klassegrænser x _{o, i} :

Densitetsfordelinger

Lineær densitet fordelingskurve

Hvis forskellen mellem proportioner Q _{r fra} den ækvivalente diameter x _{U, I} (nedre grænse for klassen i ) og x _{o, i} (øvre grænse for klassen i) beregnes, så:

${\ displaystyle \ Delta Q_ {r} (x_ {u, i}, x_ {o, i}) = Q_ {r} (x_ {o, i}) - Q_ {r} (x_ {u, i}) }$

Den diskrete densitetsfordeling q _r (x) defineres således som følger:

${\ displaystyle q_ {r} (x_ {u, i}, x_ {o, i}) = {\ frac {\ Delta Q_ {r} (x_ {u, i}, x_ {o, i})} { \ Delta x_ {i}}}}$

For bredden af ​​klasse i gælder følgende :

${\ displaystyle \ Delta x_ {i} = x_ {o, i} -x_ {u, i}}$

I tilfælde af en differentiabel kumulativ fordeling Q _r (x) , fordelingen tæthed er den 1. afledede af Q _r (x) :

${\ displaystyle q_ {r} (x) = {\ frac {dQ_ {r} (x)} {dx}}}$

Den lineære densitetsfordeling q _r (x) har - forudsat at x er en ækvivalent diameter - enheden [m ^-1 ]. Følgende diagram viser en typisk kurve for densitetsfordeling:

Det markerede område er andelen af partiklerne ΔQ _r indeholdt i intervallet Δx _i = x _{o, i} - x _{u, i} , hvis størrelse eller ækvivalent diameter x er mellem x _{u, i} og x _{o, i} . På grund af normaliseringen af den kumulative fordeling Q _r , området under tæthedsfordelingen kurve er lig med 1:

${\ displaystyle \ int _ {x _ {\ mathrm {min}}} ^ {x _ {\ mathrm {max}}} q_ {r} (x) \; dx = Q_ {r} (x _ {\ mathrm {max} }) - Q (x _ {\ mathrm {min}}) = 1}$

I praksis skal du dog normalt håndtere diskrete værdier , dvs. individuelle værdier, for densitetsfordelingen. Tæthedsfordelingen som funktion er ikke eksplicit kendt. Der anvendes derefter flere anvendelsesmuligheder:

Histogram :

Densitetsfordelingen antages at være konstant i intervallet Δx _i . Resultatet er et rektangulært område:

${\ displaystyle \ Delta Q_ {r, i} = q_ {r} (x_ {u, i}, x_ {o, i}) \ cdot \ Delta x_ {i}}$

Travers :

Værdien af fordelingen tæthed q _r for intervallet (x _{U, I} , x _{o, i} ) er afbildet på placeringen af aritmetiske klasse center , dvs. H. ved x _{m, a} = (x _{o, i} + x _{u, i} ) / 2 . De resulterende datapunkter er lineært forbundet som en tilnærmelse.

Spline interpolation :

Som med polygonforløbet er værdien af ​​densitetsfordelingen afbildet på stedet for det aritmetiske klassecenter. Værdierne forbindes derefter med en polynomial tilnærmelsesfunktion (spline). Det skal bemærkes, at de værdier, der er interpoleret på denne måde, er af matematisk og ikke fysisk oprindelse.

• 

  histogram

• 

  Travers

• 

  Spline

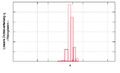
Tæthedsfordelingen q _r (x) viser meget ofte formen på en Gaussisk klokke. Hvis fordelingen kun har et maksimum, taler man om en monomodal fordeling. Med to maksima er fordelingen bimodal. Abscissaværdien for det største maksimum kaldes tilstandsværdien.

Densitetsfunktion af partikelantalskoncentrationen

Inden for atmosfæriske aerosoler anvendes densitetsfunktionen af ​​partikelantalskoncentrationen i stedet for den rene densitetsfunktion. Til dette formål multipliceres densitetsfordelingen med den målte partikelantalkoncentration.

${\ displaystyle q_ {0} ^ {*} (x) = q_ {0} (x) \ cdot c_ {n}}$

Fordelen ved denne form for repræsentation er den direkte sammenlignelighed af partikelstørrelsesfordeling og partikelantalskoncentration af aerosoler.

Logaritmisk densitetsfordeling (transformeret densitetsfordeling)

Repræsentationen af ​​en lineær densitetsfordeling q _r er upraktisk, hvis området for de tilgængelige ækvivalente diametre strækker sig over mere end et årti. I denne sammenhæng taler man om en bred fordeling. I disse tilfælde tilrådes det at bruge en logaritmisk opdelt abscisse, da oversigten da er meget lettere. Den logaritmiske densitetsfordeling er markeret med q _r * eller q _{r, log} . Værdien af ​​densitetsfordelingen q _r * for intervallet (x _{u, i} , x _{o, i} ) er tegnet ved placeringen af ​​det geometriske klassecenter , dvs. H. på:

${\ displaystyle x_ {m, i, g} = {\ sqrt [{2}] {x_ {o, i} \ cdot x_ {u, i}}}}$

I praksis har det logaritmiske plot ofte vist sig at være fordelagtigt sammenlignet med det lineære plot. Følgende diagram viser et logaritmisk plot af en snæver fordeling.

Fra et matematisk synspunkt er det logaritmiske plot en erstatning for abscissen. Følgende gælder generelt:

${\ displaystyle q_ {r} ^ {*} (s) = q_ {r} (x) \ cdot {\ frac {\ mathrm {d} x} {\ mathrm {d} s}}}$

og med s = lg x = (ln x ) / 2.3026 får man for konverteringen

${\ displaystyle q_ {r} ^ {*} (\ lg \, x) = 2 {,} 3026 \ cdot x \ cdot q_ {r} (x)}$

Det skal understreges, at den logaritmiske erstatning af abscissen fører til en ændring i kurvens form, dvs. H. blandt andet, at tilstandsværdien skifter. Normaliseringsbetingelsen er derimod altid opfyldt.

litteratur

• DIN 66143 Repræsentation af kornstørrelsesfordelinger (partikelstørrelse) - kraftnet . 1974.
• DIN 66144 Repræsentation af kornstørrelsesfordelinger (partikler) - logaritmisk normalfordelingsnetværk. 1974.
• DIN 66145 repræsentation af kornstørrelsesfordelinger (partikler) - RRSB-netværk. 1976.
• DIN 66160 måling af disperse systemer, vilkår.
• DIN 66161 partikelstørrelsesanalyse, symboler, enheder.
• DIN ISO 9276-1 Præsentation af resultaterne af partikelstørrelsesanalyser. Del 1: Grafisk repræsentation.
• Matthias Stieß: Mekanisk procesteknik. Bind 1. 2., revideret udgave. Springer, Berlin et al. 1995, ISBN 3-540-59413-2 (3., fuldstændig revideret udgave, som: Mechanische Verfahrenstechnik. Bind 1: Partikeltechnologie. Ibid. 2009 (udgivet 2008), ISBN 978-3-540-32551-2 ).
• Albrecht F. Braun: Den genetiske fortolkning af naturlige dynger ved hjælp af det logaritmiske kornnetværk ifølge ROSIN, RAMMLER og SPERLING (DIN 4190). I: Journal of the German Geological Society. Bind 126, 1975, ISSN  0012-0189 , s. 199-205, abstrakt .